統計検定2級の過去問解説。2018年11月に実施された問題

2018年11月に実施された統計検定2級の過去問解説です。

問題は、統計検定のHPにありますので、そちらからダウンロードしてください。

 

2018年6月に実施された統計検定2級の過去問の解説もしています。

2017年11月に実施された統計検定2級の過去問の解説もしています。

 

統計検定2級2018年11月の過去問：問１（１）

この問題で重要なことはただ一つ。

ということ。

これさえわかればOKです。

 

（ア）：100-(85.1+2.1) = 12.8%

（イ）：100-(76.6+17.0+2.1) = 4.3%

 

 

統計検定2級2018年11月の過去問：問１（２）

箱ひげ図の問題ですが、実は最大値に着目すれば解ける問題。

各年代の最大値は以下の通りですよね。

1952年の最大値：60校以上80校未満

1985年の最大値：100校以上120校未満

2017年の最大値：120校以上140校未満

 

ということで、箱ひげ図の縦軸のスケールに着目しましょう。

縦軸の一番大きい数字が70であるAが1952年

縦軸の一番大きい数字が100であるBが1985年

縦軸の一番大きい数字が140であるCが2017年

となります。

 

 

統計検定2級2018年11月の過去問：問１（３）

四分位範囲とは、全データを小さい（大きい）順に並べて、下（上）から25%の点と75%の点の間のことをいいます。

箱ひげ図では、箱の部分が四分位範囲。

そのため、A,B,Cの順で四分位範囲が大きくなっていることが分かります。

そのため、Iは×。

 

1952年の最大値は60校以上80校未満、1985年の最大値は100校以上120校未満ですから、1952年の最大値は1985年の最大値の半分以下、というのは間違いです。

そのため、IIは×

 

箱ひげ図において、中央値は箱の中の横線です。

そのため、A,B,Cの順に中央値が大きくなっています。

そのため、IIIは〇。

 

 

統計検定2級2018年11月の過去問：問2

この問題で重要な知識は、相関係数は直線関係の指標である、ということ。

つまり、二次曲線の関係があったとしても、相関係数の絶対値は小さくなります。

 

“男性・正社員”では、50-54歳を頂点とした、放物線（二次曲線）の形をしています。前述の通り、相関係数は「直線関係」を表している指標です。そのため、このグラフは相関係数のみで判断してはいけません。

そのため、Iは〇。

 

“女性・正社員”についても、“男性・正社員”と同様に50-54歳を頂点とした放物線になっています。ですが、20-24歳から50-54歳までを見ると、比較的直線関係が見えています。ということであれば、69歳までの全体の相関係数よりも絶対値は大きくなるはず。

そのため、IIは×。

 

相関係数は、ｘが大きくなるとｙがどれだけ上がるか、ということを反映した指標ではありません。繰り返しになりますが、直線関係がどれほどあるか、という指標です。

そのため、IIIは×。

ちなみに、ｘが大きくなるとｙがどれだけ上がるか、ということを調べたい場合には、回帰分析を行います。

 

 

統計検定2級2018年11月の過去問：問3（１）

変化率は、以下の式で求めることができます。

前月からの変化率＝（求めたい月のデータ　-　前月のデータ）/前月のデータ×100

そのため、（ア）をxとすると、4.98=(111.7-x)/ｘ*100を求めればOKです。

ということで、106.4になります。

 

 

統計検定2級2018年11月の過去問：問３（２）

３項移動平均とは、軸となるデータ（今回の問題では2017年10月）と、その前後のデータの平均値です。

そのため、2017年9月、10月、11月の3つのデータの平均値になります。

つまり、（110.3+107.9+109.5）/3が正解です。

 

 

統計検定2級2018年11月の過去問：問4

ラスパイレス指数の計算式を知っていれば解ける問題です。

つまり、今回の問題だとこのような式になります。

 

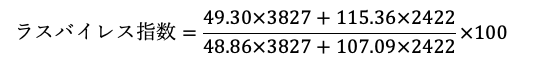
統計検定2級2018年11月の過去問：問5

抽出に関する基本問題です。

I：◯

これは正しいです。

II：×

層の標本サイズが同じなら、層別しない抽出方法と同程度の分散を期待することができます。

ですが、標本サイズが違う場合には、平均値の分散は大きくなります。

III：◯

これは正しいです。

 

 

統計検定2級2018年11月の過去問：問6

このような、抽出を何段階かに分けて実施することを多段抽出と呼びます。

この問題では、２段階（市区町村と世帯）の抽出をしているため、２段抽出と呼びます。

 

統計検定2級2018年11月の過去問：問7（１）

抽出した箱が工場Aからのものである確率は、0.7である。

更に、この箱にカモノハシの絵がプリントされているのは0.02である。

ということは、抽出した箱がAであり、更にカモノハシの絵がプリントされている確率は、0.7×0.02=0.014である。

同様に、抽出した箱がBであり、更にカモノハシの絵がプリントされている確率は、0.3×0.08=0.024である。

よって、抽出した箱にカモノハシの絵がプリントされている確率は0.014+0.024=0.038となる。

 

 

統計検定2級2018年11月の過去問：問7（２）

条件付確率の定義は以下の通りです。

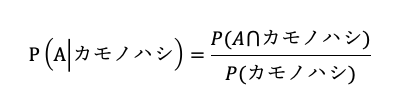
そのため、求める確率は次の通り。

 

 

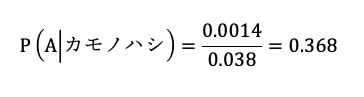
統計検定2級2018年11月の過去問：問8（１）

ちょっとだけ難しい問題です。

ですが、まずは与えられた問題の通りに計算していきます。

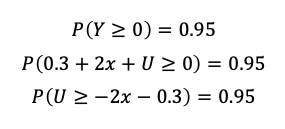
で、ここからが頭を使うのですが、Uは平均0、分散1の正規分布に従います。

つまり、正規分布表を確認して、95%よりも大きくなるUの点を探します。

すると、Uが-1.64以上となる確率は95%と確認できます。

そのため、以下の等式を解けばよいということが分かります。

 

 

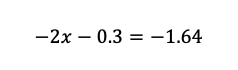
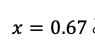
統計検定2級2018年11月の過去問：問8（２）

問題文より、以下の通り。

95%点はUが1.64の時なので、以下の式となります。

つまり、一次方程式であることがわかりました。

直線関係のグラフは1なので、答えは１です。

 

 

 

統計検定2級2018年11月の過去問：問９（１）

計算が面倒なので、ミスに注意です。

まず、2以下の目が出る確率は1/3であり、それ以外の目が出る確率は2/3です。

7回サイコロを振ってx+1回だけ2以下の目が出る確率は、以下の通りです。

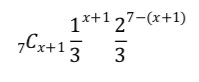
同様にして、x回だけ2以下の目が出る確率は、以下の通りです。

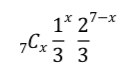
これを式展開すると、以下の通りになります。

 

 

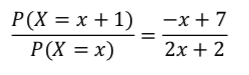
統計検定2級2018年11月の過去問：問9（２）

（１）で求めた式に0～7を代入してみます。

すると、ｘ＝２の時に最大になります。

 

 

統計検定2級2018年11月の過去問：問10

標本平均の期待値と、標準誤差の知識があれば一発で回答できます。

標本平均の期待値は、確率変数の期待値と一緒であるため、（ア）はμ。

標準誤差（標本平均の標準偏差）はσ/sprt(n)となるため、分散はその2乗。

つまり、σ2/nとなる。

 

 

統計検定2級2018年11月の過去問：問11（１）

歪度と尖度の問題です。

どちらも、正規分布の場合には０になります。

 

 

統計検定2級2018年11月の過去問：問11（２）

結構な難問でした。

確率変数Xが一様分布U(a,b)に従う時、平均値と分散は以下の定義です。

よって、一様分布U(-1,1)では、平均値が0,分散が1/3となります。

よって、問題文の歪度の定義から以下のように求めることができます。

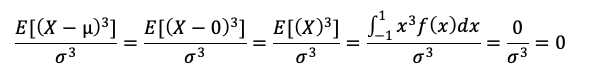
また、尖度も同様に計算すると、-1.2となります。（計算式は割愛します）

 

 

統計検定2級2018年11月の過去問：問11（３）

I：×

逆です。

右に裾が長い分布では、歪度は正の値になり、左に裾が長い分布では、歪度は負の値になります。

II：×

こちらも逆です。

正規分布よりも尖っている分布では尖度は正の値に、正規分布よりも中心部が平坦な分布では尖度は負の値になります。

III：×

自由度が大きくなるにつれて、t分布は正規分布に近づきます。すなわち、尖度は0に近づくので、絶対値は小さくなります。

 

 

 

統計検定2級2018年11月の過去問：問12

比率の信頼区間。

統計検定２級では、かなりの頻度で出題されます。

割合をpとして、信頼区間は以下の式で計算できます。（暗記しておいていいレベルです）

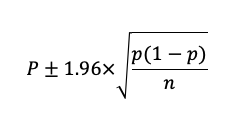
今回のデータを当てはめると、以下のようになります。

 

 

統計検定2級2018年11月の過去問：問13

t統計量の基礎問題です。

サンプルサイズをn、母平均をμ、標本平均をx、不偏分散をs2とすると、t統計量は次の式から求められます。

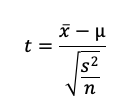
よって、t統計量は値を代入して以下のようになります。

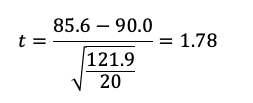
両側5%ということは、片側2.5%であるため、T分布表から自由度20-1=19の棄却域は2.093です。

そのため、棄却域＞T統計量なので棄却されません。

 

 

統計検定2級2018年11月の過去問：問14（１）

「分散が等しいかどうか」の検定は、F検定です。

覚えていただきたいのは２点。

「F統計量の式」と「自由度」です。

F統計量は以下の式で算出できます。

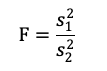
また、このときの自由度は以下の通りです。

そのため、自由度は29, 30となります。

 

 

統計検定2級2018年11月の過去問：問14（２）

検定の多重性の問題です。

３つの検定をして「１つでも有意であればよい」ときの確率を求めます。

１つでも有意であれば良い、ということを直接計算するとややこしいので、逆転の発想をします。

それは、1-（１つも有意にならない確率）を求めるということです。

１つの検定のαエラーを5%とした時、有意にならない確率は1-0.05です。

つまり、以下の式を解けば良いです。

 

 

統計検定2級2018年11月の過去問：問15（１）

「不良品、不良品でない」という２値のデータですので、二項分布が当てはまります。

二項分布は統計検定２級では必ず出題されますので、必ず理解しておきましょう。

二項分布の平均値はnpで求めることができ、分散はnp(1-p)で求めることができます。

つまり、平均値はnp=200*0.05=10であり、分散はnp(1-p)=10*0.95=9.5となります。

 

 

統計検定2級2018年11月の過去問：問15（２）

標本平均をp、母比率をp0、サンプル数をnとすると、以下の式から求めることができるz統計量は、標準正規分布に従います。

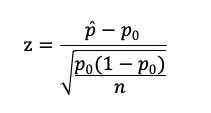
200個のうち、16個が不良品なので、標本平均は16/200となります。

そのため、z統計量は以下の通りです。

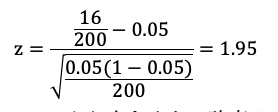
標準正規分布表を見ると、1.95より大きくなる確率は0.026であることがわかる。

 

 

統計検定2級2018年11月の過去問：問15（3）

２つの群の標本比率をそれぞれp1,p2とし、サンプルサイズをn1,n2とすると、次の式から求められるz統計量は、標準正規分布に従う。

ただし、pはプールした標本比率のこと。

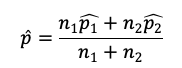
問題文より、A社の標本比率は16/200=0.08であり、B社の標本比率は17/200=0.085です。そのため、プールした標本比率は、以下の通り。

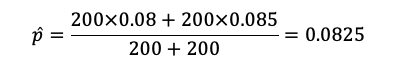
よって、zは以下の通り。

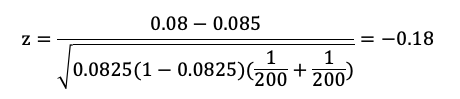
標準正規分布より、-0.18より小さくなる確率は0.43であるため、両側検定ではその2倍である、0.86がP値になります。

 

 

 

統計検定2級2018年11月の過去問：問16（１）

適合度検定において、 カイ2乗統計量は以下の通り。

よって、これを満たしているのは１のみ。

 

 

統計検定2級2018年11月の過去問：問16（２）

カイ二乗検定の自由度は、カテゴリの数-1であるため、５です。

自由度5のカイ二乗分布における上側5%点は11.07となります。

１つ前の問題で１がカイ二乗統計量でしたので、2.59<11.07より、棄却されない、という結果になります。

 

 

統計検定2級2018年11月の過去問：問17（１）

回帰分析の読み取り方です。

国の数（データの数）を読み取るには、自由度を読み取る必要があります。

自由度はdegree of freedomもしくは、DFと表記されます。

２通りの読み取り方があります。

 

１つ目は、Residual standard errorのdegree of freedomに着目する方法。

Residual standard errorとは、残差の標準誤差のことです。

この時の52 degree of freedomは、（データの数-説明変数の数-1）から算出されますので、52=X-2-1が成り立ちます。

そのため、X＝55となります。

 

２つ目は、F-statisticのDFに着目する方法です。

「2 and 52 DF」は、「説明変数の数 and 残差 DF」を示しています。

そのため同様に、52=X-2-1の関係式が成り立ちますので、X＝55となります。

 

 

統計検定2級2018年11月の過去問：問17（２）

I：×

αの推定値はInterceptの行です。

説明変数のないパラメータは日本語では「切片」と呼び、統計ソフトではInterceptと表示されますので、覚えましょう。

そのため、αの標準誤差は113.7です。

II：◯

ここで重要なのがeの読み取り方です。

統計ソフトの出力でe+は10倍を示していますので、例えばe+02であれば、10倍の10倍、つまり100倍するということです。

一方で、e-は1/10するということを示していますので、例えばe-02であれば1/100するということです。

それを念頭におくと、全てのパラメータで0.05を下回ることがわかりますので、有意水準5%で0ではないという結果になります。

III：×

自由度調整済み決定係数は、Adjusted R-squaredを見ます。

すると、0.8141ですので、間違いです。

自由度を調整しない決定係数は、Multiple R-squaredになります。

 

 

統計検定2級2018年11月の過去問：問17（３）

I：◯

人口密度（Population）の点推定値（Estimate）を見ると、マイナスの値になっています。

そのため、人口密度が高い国では、自動車普及率は低い傾向がある。

II：◯

１人当たりGDPの点推定値（Estimate）を見ると、プラスの値になっています。

そのため、１人当たりGDPが高い国では、自動車普及率は高い傾向がある。

III：◯

得られた推定値を回帰式に代入すると、450となる。

 

 

統計検定2級2018年11月の過去問：問18（１）

I：◯

残差の標準誤差²=残差平方和/(サンプル数-説明変数の数-1)という関係を知っているかどうか、という問題でした。

この方程式を解くと、0.608²×(5-1-1)=1.1となります。

II：×

単位を変えても、t値は変わりません。

III：◯

単位を変えると、推定値は変わります。

 

 

統計検定2級2018年11月の過去問：問18（２）

I：×

上記の問題と同様に、推定値は単位を変えれば変わります。

そのため、説明変数が不要かどうかは、推定値が0に近いかどうは関係ありません。

一般的には、P値を確認して判断します。

II：×

説明変数間の相関が高い場合には、多重共線性の問題が発生します。

標本サイズは関係ありません。

III：×

得られたP値（0.559）>有意水準（0.05）であるため、棄却されません。

 

 

統計検定2級2018年11月の過去問：問18（３）

I：×

説明変数の数が異なれば、得られる推定値は異なります。

II：◯

これはその通りです。

III：×

有意ではないため、xが1万円大きい時yが6.462万円小さくなる、ということはできません。