ヒストグラムからわかることは？特徴や見方など読み取り方を例を用いてわかりやすく説明！

・ヒストグラムとは？

・ヒストグラムからわかることって何？

・ヒストグラムの特徴は？

・ヒストグラムの作り方がわからない・・・

 

私の元に、ヒストグラムの質問が寄せられることが多いです。

ヒストグラムは、データを正規分布かどうかを可視化するのにとても有用なグラフ。

この記事では、とても有用なヒストグラムをわかりやすく徹底解剖します！

ヒストグラムのエクセルでの作り方からその解釈方法まで、徹底解剖します！

 

ヒストグラムからわかること：データを可視化することで気付くことがある

私たちは、日常的に多少なりともデータを扱っています。

もしあなたが商売を営んでいるなら、売り上げや仕入れ値や経費のデータを。

もしあなたが学生なら、テストの成績データが進学や卒業に関係する重要なデータです。

もしあなたがサラリーマンであれば、毎年の健康診断のデータも、今後の健康を左右する大事なデータです。

 

しかし、データは生のまま（単純な数字の羅列）ではそこから何も見出せません。

生のデータは単なる「事実」を示しています。

ただ、事実からだけでは何も生まれません。

そこで私たちは、生のデータを他のデータと比較したり、生のデータを加工したりして、何かしらの示唆を得ようとするのです。

 

下表は、50人分の大学生の男子の身長（cm）データです。

このデータを見ただけで、あなたは何かを引き出せますか？

 

169.1	164.4	171.7	176.6	176.3
178.8	160.0	169.4	175.8	165.3
167.2	162.4	161.6	165.8	166.8
160.3	167.8	168.6	171.1	168.7
168.9	168.7	176.9	170.1	169.6
168.0	180.0	174.7	181.9	167.4
178.5	162.8	173.1	174.8	179.7
170.1	168.0	173.7	168.7	174.1
163.6	166.4	163.2	168.8	170.3
170.6	169.0	181.0	162.1	167.0

 

結構難しいですよね。

データの数が１０個以下ぐらいなら、なんとか生データを見て解釈可能かもしれません。

ですがデータがそれ以上になると。。

やっぱり何かしら加工してあげて、解釈する元になる代表値を出して解釈する必要がありますね。

 

ヒストグラムでわかること1：数字は同じではなくバラバラしている

50個のデータを見て解釈できることは難しそうでした。

ですが一つだけ言えることがあります。

 

それは、「身長は全員同じではなく、バラバラの数値である」ということです。

 

すーーーーっごく当たり前のことを言っています。

ですが、すーーーーーっごく大切なことです。

 

なぜなら、この「バラバラの数値をとっている」事実があるために「よし、統計を使ってみよう！」ということになるからです。

そして、バラバラの数値を取っていることを、専門用語で「分布する」と言います。

 

さて、もうちょっと50人のデータを見てみると、もう一つ言えることがありそうです。

それは「バラバラだけど、ある数値の周辺でバラバラになっていそうだ」ということです。

 

つまり、100センチ以下の身長の人は一人もいないし、200センチを超える人もいませんよね。

そして、なぜか160センチ〜180センチぐらいの間でバラバラしてそうです。

 

そう、バラバラな中にも上記のような「特徴」がありそうです。

この特徴を専門用語で「分布の特性」と言います。

 

ヒストグラムでわかること2：数字は闇雲にバラバラしているわけではない！

つまりデータは「何らかの特徴を持った上でバラバラしている」ということが言えます。

そして、その「特徴」が何なのかなー、というのを調べるために統計を使うのです。

つまり、「データとして並んでいるたくさんの数字を、何かの基準で整理整頓して、意味のある情報を取り出してあげる」ということをする。

そのために、２つの方法が考えられます。

 

1. グラフ化してその特徴を捉える
2. １つの数字で特徴を代表させる（→この代表する数字を統計量と言います。）

 

今日のメイントピックである「ヒストグラム」は、１つ目の方法である「グラフ化してその特徴を捉える」という方法に最も合致した図式化方法なのです。

つまり、ヒストグラムからわかることは「データがどれぐらいばらついているのか、そしてその特徴とは何か？」ということがわかるのです。

 

ヒストグラムと同様に、箱ひげ図もデータを可視化する観点ではかなり有用なので、併せて理解していきましょう。

 

ヒストグラムの作り方！作り方がわかると特徴がわかるので読み取り方もわかる！

ヒストグラムはデータの特徴を捉えるのに最適な図式化方法であることを解説しました。

じゃあ、ヒストグラムを作ってみよう！

というのがここでのミッションです。

なぜなら、作り方がわかると、ヒストグラムの意味やどこまで特徴がわかるのか、といった読み取り方がわかるようになるからです。

 

つまり、何かしら身に付けたい場合には、それをアウトプットしてみることが大事です。

ヒストグラムを知りたければ、ヒストグラムをアウトプットしてみることが大事。

つまり、ヒストグラムを実際に作ってしまう、ということが大事になるのです。

 

ヒストグラムの特徴

答えから言うと、ヒストグラムはこういうものです。

さっきの、50人のデータをヒストグラムにしています。

 

 

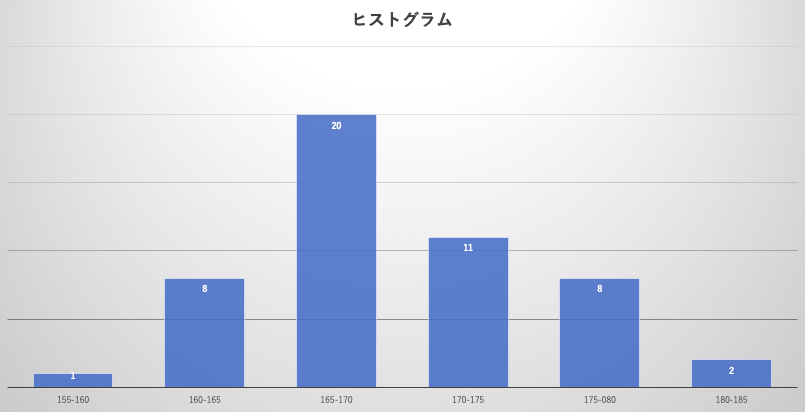
横軸が階級（データを小区間で区切ったもの）で、縦軸が度数（人数）です。

つまり、階級と度数の二つがあればヒストグラムはできるってことです！

では階級と度数の二つ用意すると決まったので、実際に作ってみましょう！

 

ヒストグラムをエクセルで作ってみる！たった3ステップで簡単に作成可能

生データからヒストグラムを作るまでには、3ステップでできます。

作成時間は２分です。

（実際に、さっきのヒストグラムを作るのに２分かかりました。）

エクセルに慣れている人なら１分かからないのでは？と思います。

 

 

なにも難しいことはありません。

３回ぐらい作ったら、もう何も見なくても出来るようになるでしょう。

 

ヒストグラムの作り方1：データの最小値と最大値を確認する

ヒストグラムを作り方のステップ1は、データの最小値と最大値を確認することでした。

そのため、実際に作る時にもデータの最小値と最大値を確認しましょう。

 

先ほどの、50人の大学生の身長のデータがこのようにエクセルにあるとします。

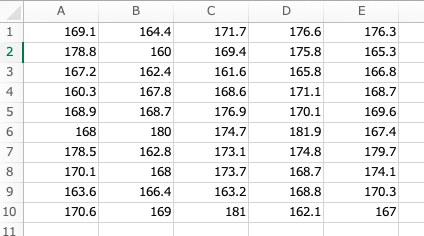
すると、最小値は「=MIN(A1:E10)」で求めることができて、最大値は「=MAX(A1:E10)」で求めることができますね。

 

ヒストグラムの作り方2：おおよそ範囲が最大値と最小値になるような範囲を決め、それを5~8の小区間に区切る

次のステップは、おおよそ範囲が最大値と最小値になるような範囲を決め、それを5~8の小区間に区切るということでした。

ステップ1で、最小値は160.0、最大値は181.9でしたね。

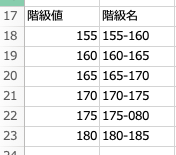
ということで、おおよその範囲を155〜185とします。

そして、小区間を5センチ刻みにしましょう。

 

エクセルでは、このように手入力で用意します。

 

ヒストグラムの作り方3：各階級に入るデータの数をカウント

ステップ2まで終われば、あとは数を数えるだけです。

エクセルでは、少々工夫が必要ですね。

エクセルでは=countif()という関数を駆使します。

この関数がやっていることを日本語に直すと、以下の通りです。

 

155センチより大きい人数を全て数え、そこから160センチより大きい人数を引く

 

これを、全ての階級値に対して実施します。

すると、各階級の人数を計算することができます。

 

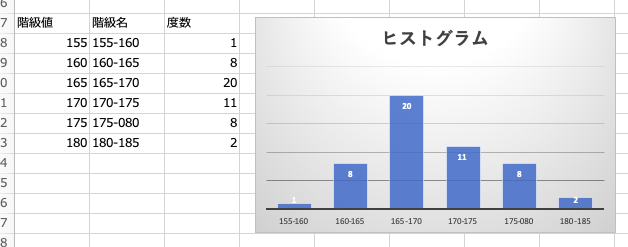
あとは、棒グラフを適用するだけです。

エクセルの「挿入」→「2-D縦棒」を選択します。

すると、以下のヒストグラムが作成できます。

 

 

ヒストグラムから何がわかる？特徴を読み取ってみよう！

さて、あなたが丹精込めて作ったヒストグラム。

ここから何がわかるでしょうか？

もう一度ヒストグラムを再掲してみます。

 

 

実は二つの特徴が見えて来るのです。

 

 

 

今までをまとめると、ヒストグラムを作ることによって以下の３つの特徴がわかったのです。

 

 

このような特徴は、生データをみると全くわからなかった特徴。

つまり、統計を使うことによって、細部は犠牲にするが、データの特徴を浮き彫りにしてくれる便利なツール。

ヒストグラムは基本的にデータが正規分布に従うかどうかを確認する手段としても使っていいと思います。

2群間の比較をする時にもヒストグラム作成は有効なので、ぜひマスターしておきましょう！

 

ヒストグラムに関してまとめ

生データを見ただけではわからない。

だが、統計を使うことで、データの特徴をつかむことができる。

ヒストグラムは3ステップで作成可能であり、データの特徴を視覚として捉えることができる。

男子大学生の身長を例にすると、以下の特徴が見える。

 

1. どんな数値も可能ではなさそう。
2. ある身長の付近にデータが集中する。
3. 集中した部分から、左右対象に度数が減っている。

 

どうでしたか？

この記事があなたの疑問を解決したなら嬉しいです！