箱ひげ図とは？見方やエクセル作り方まで解説！外れ値や平均値も確認できる

統計を勉強していると、必ず出てくる箱ひげ図。

統計検定２級でも、必ずといっていいほど問題が出題されます。

箱ひげ図はデータを可視化するのに、かなり有用なグラフです。

ヒストグラムと同じぐらい、個人的にはかなり有益だと思っている箱ひげ図。

 

でも、箱ひげ図を使ったことがなければ、

 

・箱ひげ図とは？

・箱ひげ図ってどんなときに使えるの？

・箱ひげ図の見方は？

 

といったことが疑問になりますよね。

 

ということで、この記事では箱ひげ図の読み取り方や、どんなデータに使えるのか、そして最後にはエクセルでの箱ひげ図の作成方法までお伝えします。

 

箱ひげ図とは？連続量を可視化するのに有益なグラフ

まず、箱ひげ図は連続量を可視化するのに有益なグラフです。

このような図を見たことありますか？

これが箱ひげ図というものです。

 

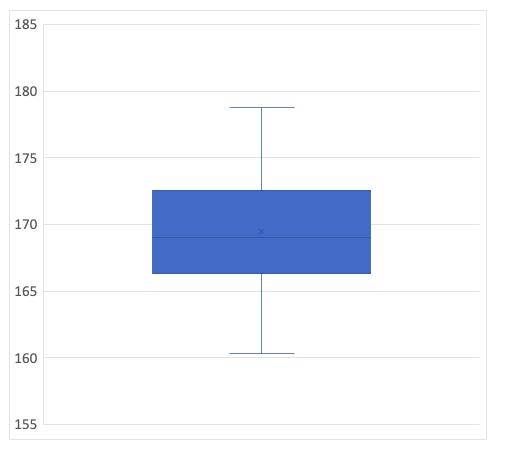
このグラフは、かなり使えます。

私も実データを解析する際には、必ずと言っていいほど使いますね。

 

で、連続量の可視化の方法として、もう一つ有名なグラフがありますよね。

あなたは答えられますか？

 

そう、ヒストグラムです。

ヒストグラムと箱ひげ図の2種類さえ覚えておけばいい、というぐらい、この2つは大切です。

 

箱ひげ図とヒストグラムの使い分けは？

箱ひげ図とヒストグラム。

どちらも連続量を可視化するのに有益なグラフ。

じゃあここで１つ疑問が浮かびます。

 

「箱ひげ図とヒストグラムってどう使い分けるの？」

 

ということです。

結論からいうと、私の使い分け方はこうですね。

 

• ヒストグラム：データが正規分布に従ってそうか？をざっくりと確認したいとき。
• 箱ひげ図：データのバラツキ度合いを知りたいとき

 

ヒストグラムを確認するときは、そのデータが正規分布に従っているかどうかを確認する時に使います。

正規分布なのか、それとも右に裾を引いているのか。

そんなことをざっくりと把握したいときに使っています。

 

データが正規分布っぽいかどうかを確認することって、実はかなり重要です。

というのも、平均値が信頼のおける値なかどうかにもかかわってくるので。

 

一方、箱ひげ図を確認するときは、データのバラツキ度合いを知りたいときに使います。

後で詳しく説明しますが、箱ひげ図を構成しているのは「中央値」「最大・最小値」「四分位範囲」「外れ値」です。

そのため、データがどれだけの範囲にありそうなのかな？というのを把握するのに最適なグラフなのです。

 

もちろん、ヒストグラムと箱ひげ図の両方を確認することは有用です。

ですが、他の人に見せると「どっちのグラフを見たらいいの？」としばしば聞かれますので、ちゃんと使い分けに関して整理しておきましょう。

 

 

箱ひげ図の見方：パーセント点や外れ値を確認できる

箱ひげ図を説明する前に、まずは「パーセント点（パーセンタイル）」について解説します。

パーセント点を知らないと、箱ひげ図を理解できませんから。

パーセント点とは以下のような点です。

 

 

つまり、０パーセント点＝最小値を表しますし、１００パーセント点＝最大値となります。

 

例えば、30パーセント点といわれた時には、以下のような図になります。

 

 

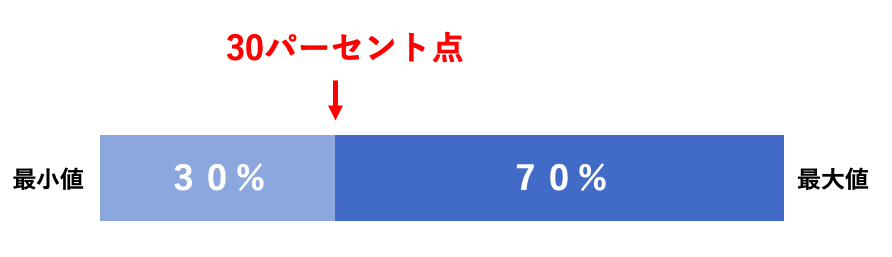
箱ひげ図に出てくる四分位数を理解する

箱ひげ図には、四分位数の情報が含まれています。

四分位数とは、「データを４分割する数」と言い換えることができます。

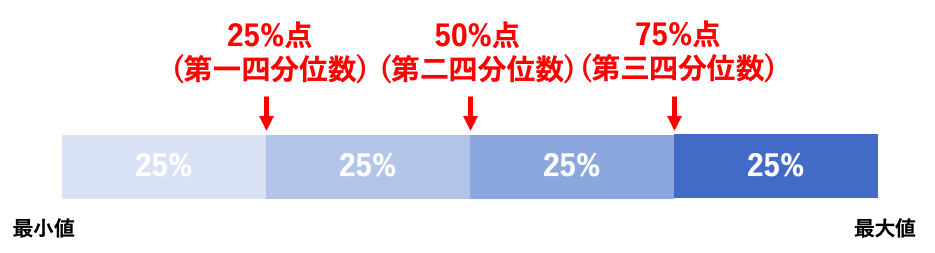
つまり、「最小値〜データの25%点」「データの25%点〜データの50%点」「データの50%点〜データの75%点」「データの75%点~最大値」と、データを４つに分けるときの25%点、50%点、75%点のことです。

四分位数は、データを小さい順に並べて、小さいものから以下の通りに名前が付けられています。

 

 

 

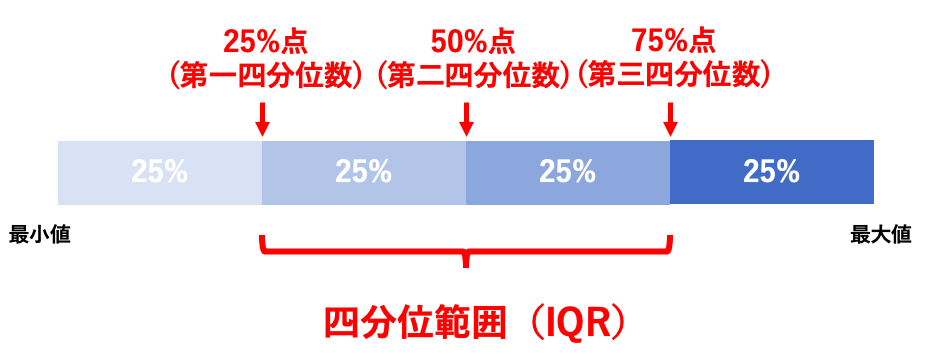
そして、第一四分位数と第三四分位数の範囲を、四分位範囲（Inter Quarter Range, IQR）と呼んでいます。

 

箱ひげ図では外れ値も確認できる

箱ひげ図では、ひげの端は必ずしも最大値、最小値を示しているわけではありません。

以下のように、ひげよりも遠いところに点が示されることがあります。

 

 

これが外れ値です。

統計ソフトによりますが、例えばエクセルの箱ひげ図のひげは、「四分位範囲の1.5倍までしか伸ばさない」と定義しています。

そのため、この範囲を超えたデータは外れ値とみなされます。

 

今までの知識を箱ひげ図に当てはめる

最小値、最大値、四分位範囲が理解できたところで、これらを箱ひげ図に当てはめてみます。

箱ひげ図に当てはめると、以下の通りになります。

 

 

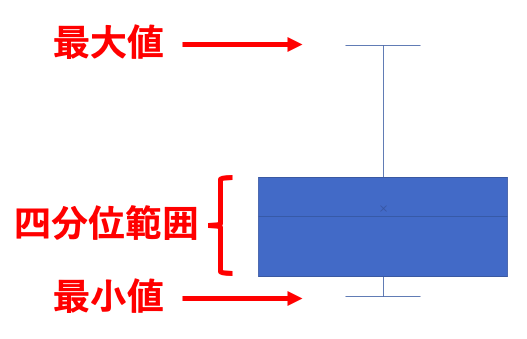
箱ひげ図の箱の部分が四分位範囲、ひげの部分が「最小値〜データの25%点」「データの75%点~最大値」を示していることになりますね。

 

そして読み取るのに重要な部分。

箱ひげ図が「最小値〜データの25%点」「データの75%点~最大値」「四分位範囲」を示しているのであれば、以下のA、B、C、Dの4区間のなかには、それぞれ同じ数だけデータが入っているということ。

 

 

しかし、同じデータの数でも、その区間の長さが違いますよね。

だから、データのばらつき具合を知ることができるということです。

例えば、区間Aと区間Bでは、区間Bの区間が短いことからよりデータが集中していることが分かります。

 

 

箱ひげ図をエクセルで作成する方法

箱ひげ図がどんなグラフか、そしてどんな時に有益なグラフなのかが分かったところで、実際にエクセルで作成してみます。

データは、ヒストグラムを作成した際に使用した、仮想の男子大学生50人分のデータを使用します。

 

箱ひげ図はエクセルで簡単に作成できる

簡単に箱ひげ図は作成できます。

箱ひげ図にしたいデータを選んで、「挿入」タブの「グラフ」から「箱ひげ図」を選ぶだけ。

 

 

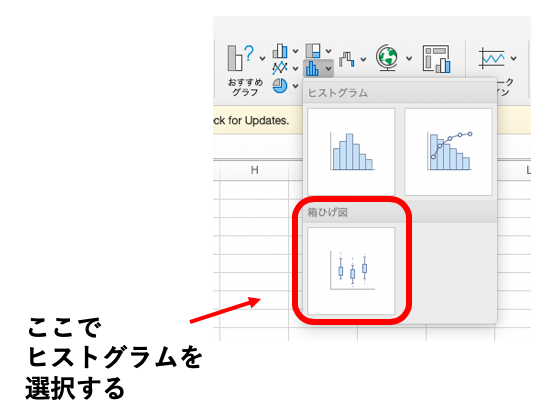
これだけで箱ひげ図が作成できました。

 

 

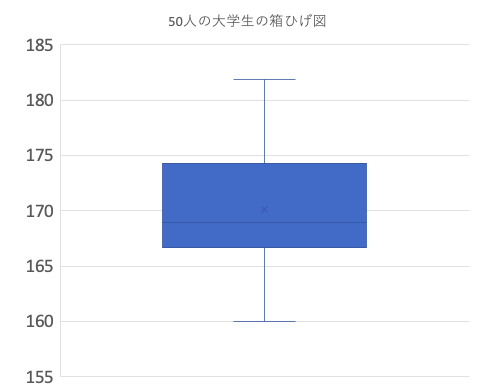
箱ひげ図で実は、平均値も確認できる

箱ひげ図は「中央値」「最大・最小値」「四分位範囲」「外れ値」を確認できるグラフでした。

で、実際にエクセルで箱ひげ図を作成しても、上記4つの指標が確認できました。

それに加えてエクセルの箱ひげ図では、新たに１つの指標が確認できます。

 

• 平均値

 

箱の中にある×の印が、平均値を示しています。

 

 

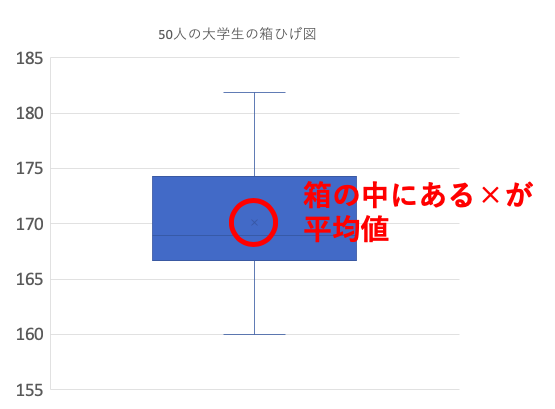
箱ひげ図とは？まとめ

• 箱ひげ図は連続量を可視化するのに有益なグラフ。
• ヒストグラムと箱ひげ図は「正規分布かどうかを確認したい」のか「データのバラツキ度合いを知りたい」のか、によって使い分ける。
• 箱ひげ図は「中央値」「最大・最小値」「四分位範囲」「外れ値」を確認できるグラフ

 

また、箱ひげ図に関しては動画でも解説しておりますので、合わせてご確認いただけると理解が進むはずです。

 

＞＞SPSSで箱ひげ図を作成する方法

＞＞JMPで箱ひげ図を作成する方法