この記事では、2018年6月に実施された統計検定2級の過去問を解説しています。
問題自体はすでにダウンロードできないため、無料のメルマガ登録でプレゼントしております。
2018年11月に実施された統計検定2級の過去問の解説もしています。
2017年11月に実施された統計検定2級の過去問の解説もしています。
統計検定2級2018年6月の過去問解説!:問1(1)
3つの箱ひげ図から適切なものを選ぶ問題。
箱ひげ図に関しては、以下の図を参照ください。
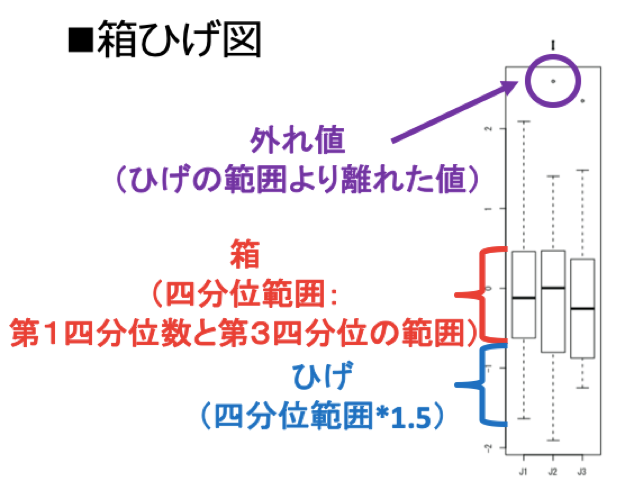
また、偏差の定義は「個々のデータ-平均値」です。
標準化とは、「偏差/標準偏差」で示されます。(標準化後のデータをZで示すことが多いです。)

標準化することによるメリットは、標準化することで平均値0、標準偏差1の正規分布データになることです。
そのため、-2〜2の間に、95%のデータが入ることになります。(正規分布の性質です。)
I:標準化得点のグラフ
縦軸が-2〜2のグラフです。すなわち、標準化得点のグラフということです。
II:偏差のグラフ
縦軸が0を中心に、約-25~30の間に散らばっています。
すなわち、偏差のグラフを示しています。
III:総得点のグラフ
縦軸が20~80の間に散らばっています。
すなわち、総得点のグラフです。
統計検定2級2018年6月の過去問解説!問1(2)
この問題では、標準化の性質を使います。
標準化することで、平均0、標準偏差1の正規分布のデータになります。
つまり、「標準偏差の2倍より離れた値があるかどうか」は、「標準化データのグラフで、-2より小さいデータまたは2より大きいデータ、があるかどうか」と言い換えることができます。
Iが標準化データのグラフですので、そこから読み取ると、1つだけ2より大きい外れ値があります。
そのため、1つ、という答えになります。
統計検定2級2018年6月の過去問解説!問2(1)
I:◯
横軸(人口)が大きくなればなるほど、縦軸(常設映画関数)が大きくなる傾向があります。
また、その傾向は直線に近いため、正の相関があると言えます。
II:◯
相関係数は外れ値の影響を受けやすいため、散布図を一緒に見る必要があります。
III:×
正の相関は見ることができました。
統計検定2級2018年6月の過去問解説!問2(2)
I:×
北海道は人口が500万人の付近にあります。
500万人の付近のデータだけを見ると、北海道は一番上にありますので、一般病院病床数は多いです。
II:◯
変動係数は標準偏差を平均で割ったものです。
人口1人当たりの一般病院病床数の変動係数は、一般病院病床数の変動係数よりも小さくなることが予想されます。
例えば、以下のようなデータがあったとします。(数値は適当です)
| 病院数 | 人口 | 1人あたりの病院数 |
| 50.0 | 5.0 | 10.0 |
| 40.0 | 3.0 | 13.3 |
| 30.0 | 7.0 | 4.3 |
| 50.0 | 5.0 | 10.0 |
| 40.0 | 8.0 | 5.0 |
| 70.0 | 5.0 | 14.0 |
このとき、変動係数(CV)は以下のようになります。
| Mean | SD | CV | |
| 病院数 | 46.7 | 13.7 | 3.4 |
| 1人あたりの病院数 | 9.4 | 4.1 | 2.3 |
1人あたりの病院数のほうが、CVが小さくなることがわかります。
III:×
人口が多い都府県に限っても、正の相関が見られます。
統計検定2級2018年6月の過去問解説!問2(3)
I:◯
偏相関係数とは、第3の因子の影響を除いた相関係数のことです。
今回の場合、常設映画関数と一般病院病床数に関して、人口の影響を取り除いた相関係数を指しています。
II:◯
残差e1と残差e2の散布図を見ると、相関があるようには見えません。
つまり、人口の影響を除くと相関が見られなくなることから、常設映画関数と一般病院病床数の相関は、擬相関であったことがわかります。
III:×
病院と併設している映画館のデータはどこにもないため、ここからは読み取れません。
統計検定2級2018年6月の過去問解説!問3(1)
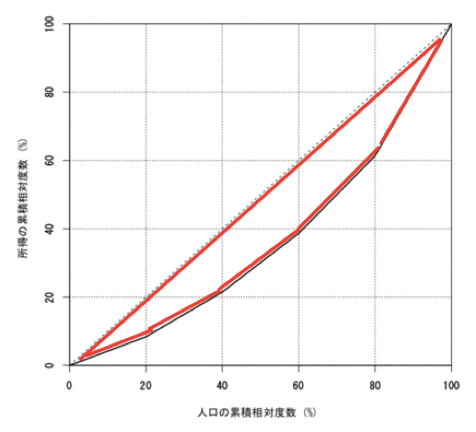
ローレンツ曲線とは、横軸に世帯(人口)の累積度数を、縦軸に所得の累積度数を示した曲線である。
ローレンツ曲線の特徴は、所得格差が存在しないなら45度線と一致し、所得に偏りがあると、曲線は下に膨らむ、ということ。
与えられた表は各階級の度数であるため、この表から累積度数分布表を作成する。
すると、以下のような表ができる。
| ~20% | ~40% | ~60% | ~80% | ~100% | |
| 日本 | 5.4% | 16.1% | 32.4% | 56.5% | 100% |
| アメリカ | 5.1% | 15.4% | 30.8% | 53.5 | 100% |
| スウェーデン | 8.7% | 23.0% | 40.8% | 63.8% | 100% |
| 中国 | 5.2% | 15.0% | 29.9% | 52.2% | 100% |
| ドイツ | 8.4% | 21.5% | 38.7% | 61.4% | 100% |
この累積度数分布表と、曲線を見比べると、ドイツが当てはまっていることがわかる。
統計検定2級2018年6月の過去問解説!問3(2)
ジニ係数とは、「45度線とローレンツ曲線の面積の2倍」で計算できる。
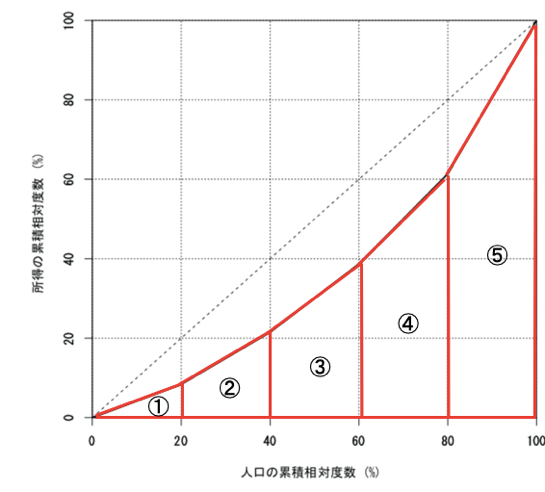
すなわち、以下の図の枠で囲んだ部分の面積の2倍である。
赤い枠の面積を直接求めることができないため、以下のように0.5 – ( ① + ② + ③ + ④ + ⑤ )を計算する。
三角形と台形の面積の計算を5つ実施し、ジニ係数を求めると、0.28になる。
統計検定2級2018年6月の過去問解説!問3(3)
I:◯
どの国も45度線より下に曲線が描かれます。
II:×
ジニ係数が大きいと、格差が大きいことを表しています。
問題文は、説明が逆です。
III:◯
スウェーデンと中国を比べると、中国のローレンツ曲線が下に描かれます。
よって、中国の方が、格差が大きいということです。
統計検定2級2018年6月の過去問解説!問4(1)
2011年の輸出物価指数の、前年からの変化率は以下の式で算出できます。
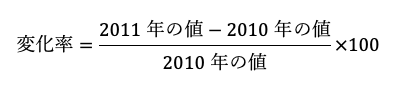
よって、以下のようになります。
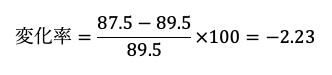
統計検定2級2018年6月の過去問解説!問4(2)
問題文を解釈できたかどうかが鍵となる。
問題文を図示すると、以下の条件を満たすrを計算するということ。
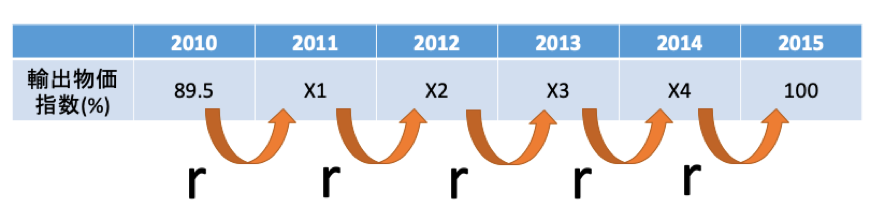
ではまず、X1を計算します。

次に、X2を計算します。
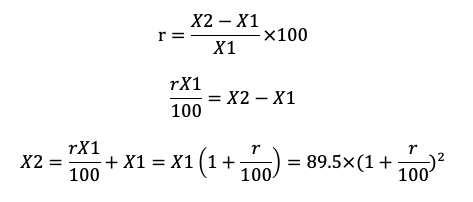
と計算することができます。
ということは、あとは2015年までの変化率を計算していけば良いということです。
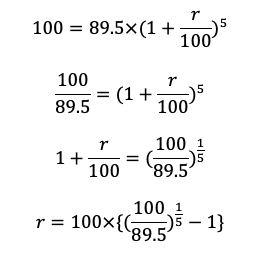
統計検定2級2018年6月の過去問解説!問5
フィッシャーの3原則とは、「繰り返し」「局所管理」「無作為化」のことです。
統計検定2級2018年6月の過去問解説!問6
抽出の問題は毎回必ずでてくるので、理解したいです。
今回の問題では、男女という「性別」というカテゴリごとに無作為抽出をしたい場合です。
この時カテゴリのことを「層」とよびます。
「層」は一般的にも使われていて、例えば「年齢層」という使い方をしますよね。
そのため、層化(層別)抽出といいます。
統計検定2級2018年6月の過去問解説!問7(1)
まず、お菓子をもらえる条件は「2回連続で勝つ」ということ。
つまり、お菓子がもらうためには、以下のうちいずれかの場合。
- 1回目と2回目に勝つ:確率はpq(独立なので、そのまま掛けて良い)
- 1回目負けて、2回目と3回目に勝つ:確率は(1-p)pq
そのため、お菓子がもらえるのは上記の2つを足したもの。
pq+(1-p)pqが正解。
統計検定2級2018年6月の過去問解説!問7(2)
T-U-Tでお菓子をもらえる確率は、(1)で計算できました。
では、U-T-Uでお菓子をもらえる確率を計算してみます。
- と同様に計算すると、qp+(1-q)qpとなります。
では、「pq+(1-p)pq」と「qp+(1-q)qp」ではどちらが大きいでしょうか。
2つの違いは、1-pと1-qのみです。
問題文よりp<qですので、1-p>1-qとなります。
つまり、T-U-Tの順番の方がお菓子をもらいやすいということがわかります。
統計検定2級2018年6月の過去問解説!問8(1)
まず必ず知っておきたいのが、正規分布の性質。
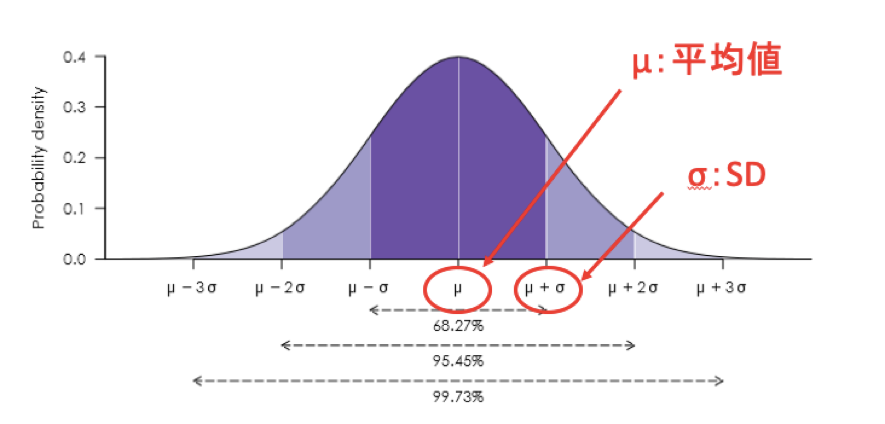
正規分布は「平均値(μ)」と「標準偏差(SD)」の2つで形が決まります。
そして、μ±SDの間には、約68%のデータが含まれています。
μ±2SDの間には、約95%のデータが含まれています。
そして、もう一つ知っておきたいのが、標準化。
問1でもさらっと出てきましたが、ここでもおさらいしましょう。

標準化をすることで、平均0、標準偏差1の正規分布(標準正規分布)のデータにすることができます。
以上の2点を知ったところで、問題です。
4,800円を標準化のデータに直します。
すると(4800-4000)/500=1.6となります。
つまり、標準正規分布で1.6以上となる確率はどれぐらいか?と問われているのと一緒です。
標準正規分布表は問題の最後の方についておりますので、1.6以上がどのぐらいの確率かを確認します。
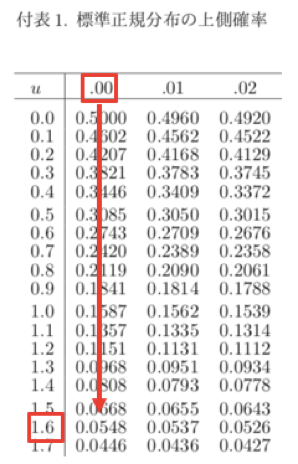
0.548なので、0.55が正解です。
統計検定2級2018年6月の過去問解説!問8(2)
この問題も、与えられた数字をZに直して、標準正規分布表と見比べる、ということをします。
つまり、最終的には以下の式に代入します。

ここで問題なのが、「今年6月と昨年6月の差の標準偏差」はどう求めるのか、ということ。
これは、分散の定義から計算します。
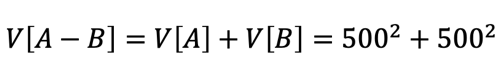
このように求めることができるので、最終的には以下の式になります。
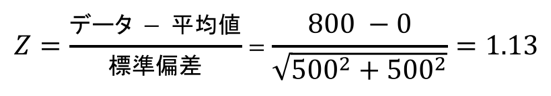
ということで、また標準正規分布と見比べて、答えは0.129となります。
統計検定2級2018年6月の過去問解説!問8(3)
難しそうに見えて、簡単な問題です。
3年分の電気料金は独立なので、その大小関係が出る確率はそれぞれ等しいです。
つまり、3年分のデータの並び順は3!=3*2*1で6通り。
そのうち、今年が一番大きい組み合わせは「前々年<前年<今年」と「前年<前々年<今年」の2通り。
つまり、2/6=1/3が正解。
問9(1)統計検定2級2018年6月の過去問解説!
平均、分散、共分散、相関の4つの定義をおさらいしましょう。
こちらの4つの定義は、暗記したほうが良いです。
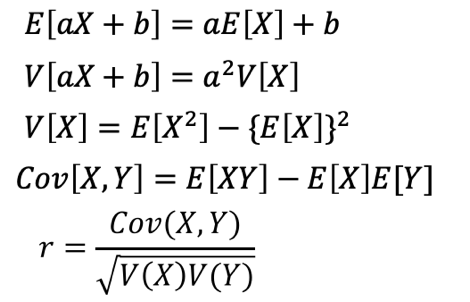
これを知っていれば、あとは当てはめるだけです。
統計検定2級2018年6月の過去問解説!問9(2)
少々複雑に思いますが、こちらの問題も上記の定義がわかっていれば解ける問題です。
計算間違いさえしなければ解くことができます。
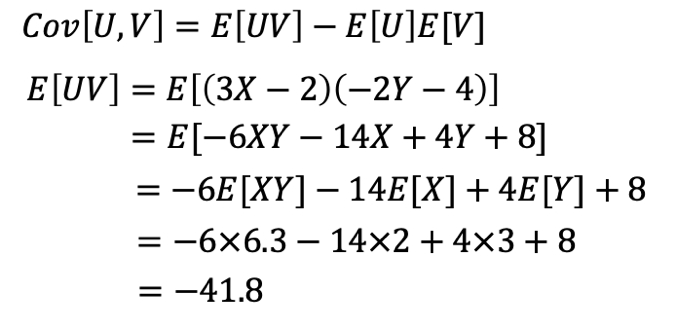
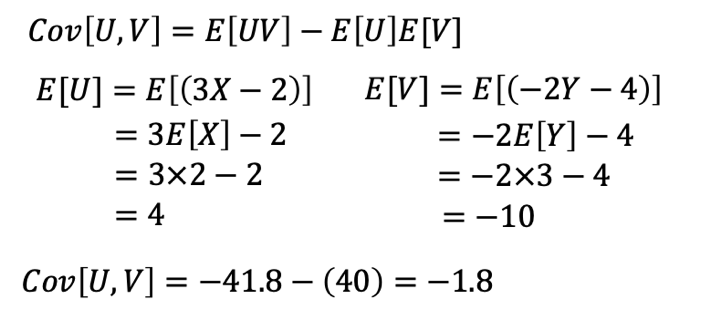
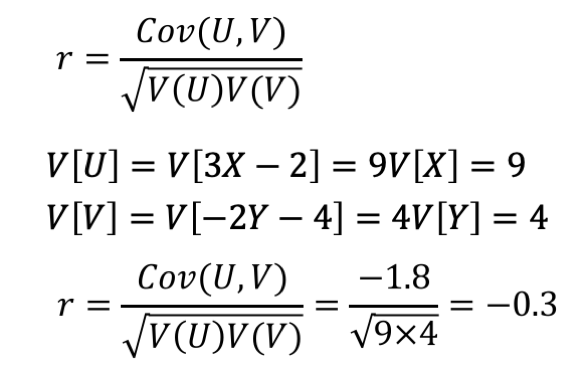
統計検定2級2018年6月の過去問解説!問10(1)
95%信頼区間の知識と、ちょっとした応用力が必要な問題でした。
まず、95%信頼区間は以下の式です。
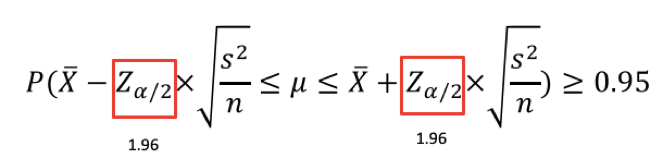
95%信頼区間の定義がわかっていれば、あとは与えられた問題文を上記の式に近づけます。
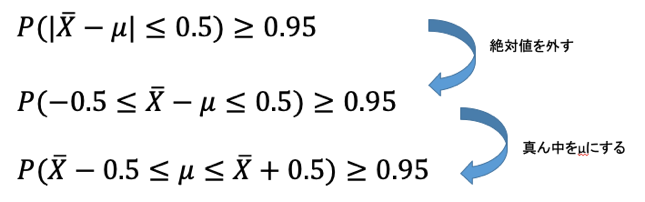
かなり、95%信頼区間の式に近づきました。
そして、上記の式と95%信頼区間の式と見比べます。
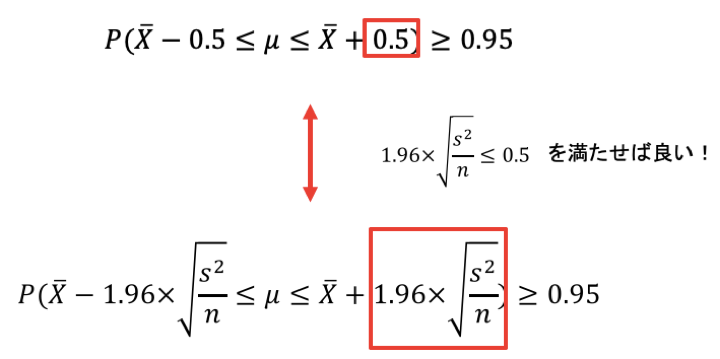
よって、あとは計算していきます。
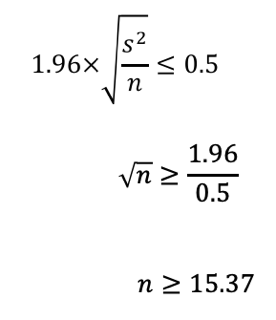
統計検定2級2018年6月の過去問解説!問10(2)
n=20が与えられたとき、T分布に従います。
つまり、95%信頼区間は以下のような式になります。
T分布表より、自由度19のt0.025は2.093です。
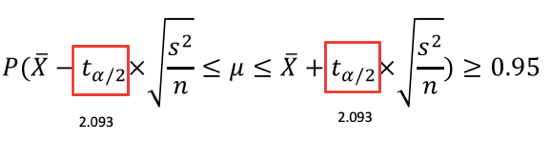
あとは、与えられた数字を代入します。

統計検定2級2018年6月の過去問解説!問11(1)
比率の信頼区間。
統計検定2級では、かなりの頻度で出題されます。
割合をpとして、信頼区間は以下の式で計算できます。(暗記しておいていいレベルです)
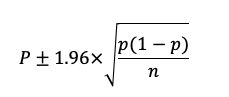
今回のデータを当てはめると、以下のようになります。

統計検定2級2018年6月の過去問解説!問11(2)
母比率の推定値は以下の式で計算することができます。

そして、標準誤差の算出には、問9で出てきた分散の定義を使います。
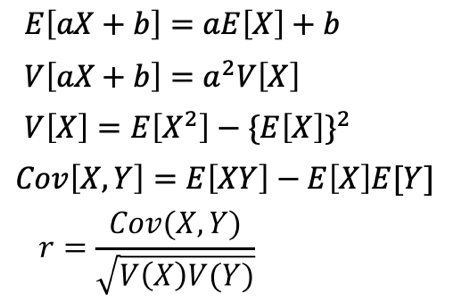
つまり、以下のようになります。
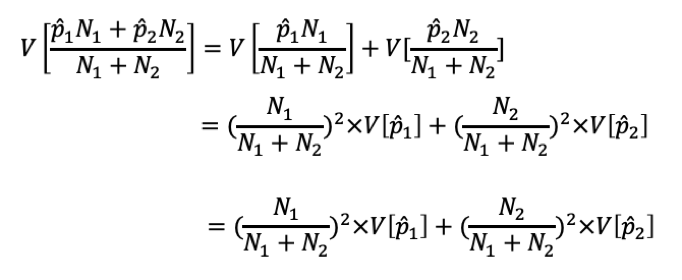
ここまでできたらあとは、標準誤差(Standard Error, SE)とは何か?がわかっていれば解くことができます。
データの標準誤差とは、推定値の標準偏差のことです。
ここはぜひ理解しておきましょう。
つまり、上記の分散をルートすれば、そのまま標準誤差になります。
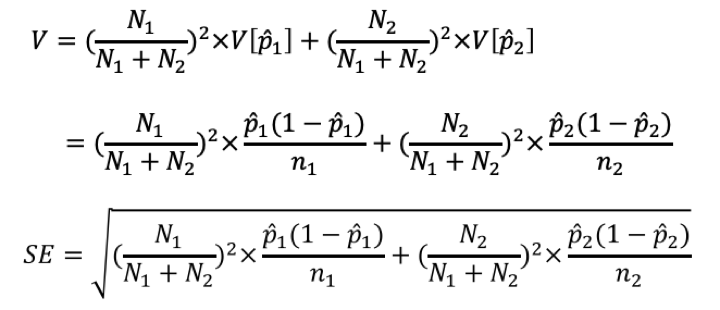
統計検定2級2018年6月の過去問解説!問12(1)
T検定の基礎知識を問う問題です。
2群のT検定の際のT統計量は以下の式で計算できます。
これは暗記していいレベルです。

そして、プールした分散とは、以下の通りです。

これがわかれば、あとは計算ミスしないようにするだけ。
計算式は割愛しますが、セリーグの不偏分散は以下の通り。
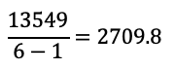
パリーグの不偏分散は以下の通り。
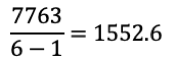
よって、t統計量は以下の通りになります。

統計検定2級2018年6月の過去問解説!問12(2)
分散分析のF値を問う問題です。
分散分析表を思い浮かべられるかどうかが鍵です。
分散分析表は以下の通りです。
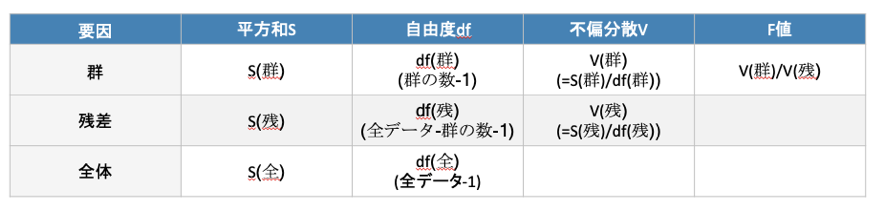
つまり、F値を算出するには群の分散と、残差の分散が必要です。
そのために、まずはそれぞれの平方和を算出します。
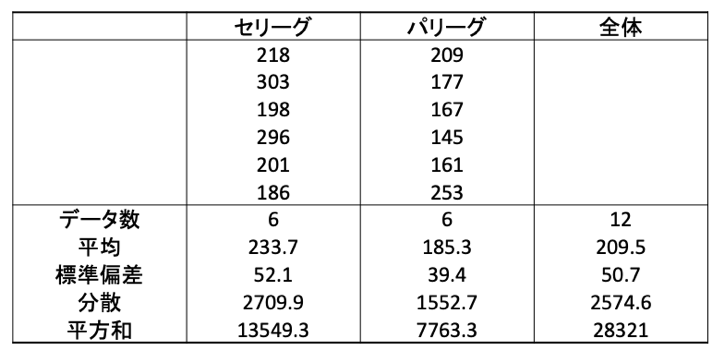
ここまでくれば、あとは分散分析表の通りに当てはめるだけです。
自由度に関しては、こちらの記事をご確認ください。
[blogcard url=”https://best-biostatistics.com/contingency/degree-freedom.html”]

統計検定2級2018年6月の過去問解説!問13(1)
まず、問題文を可視化してみます。
H0(帰無仮説)とH1(対立仮説)の数字が与えられていますので、それをそのままグラフにします。
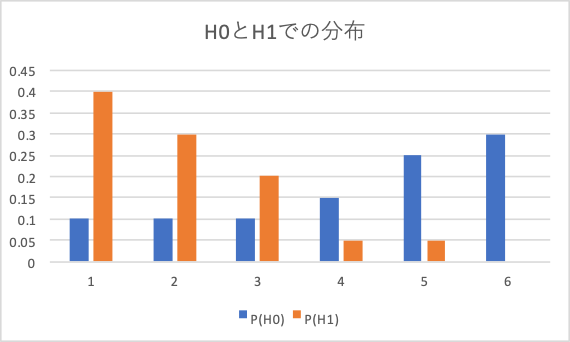
(1)ではX≦3としていますので、以下の通りの棄却域になります。
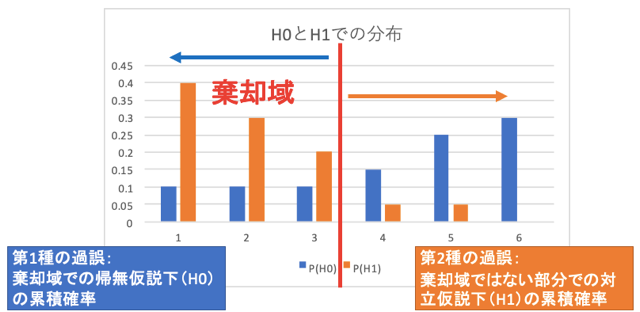
そして、第1種の過誤、第2種の過誤、検出力の用語を整理します。
- 第1種の過誤:棄却域での帰無仮説下(H0)の累積確率
- 第2種の過誤:棄却域ではない部分での対立仮説(H1)の累積確率
- 検出力:1-第2種の過誤
よって、第1種の過誤は0.1+0.1+0.1=0.3となります。
第2種の過誤は0.05+0.05=0.1となります。
検出力は1-0.1=0.9となります。
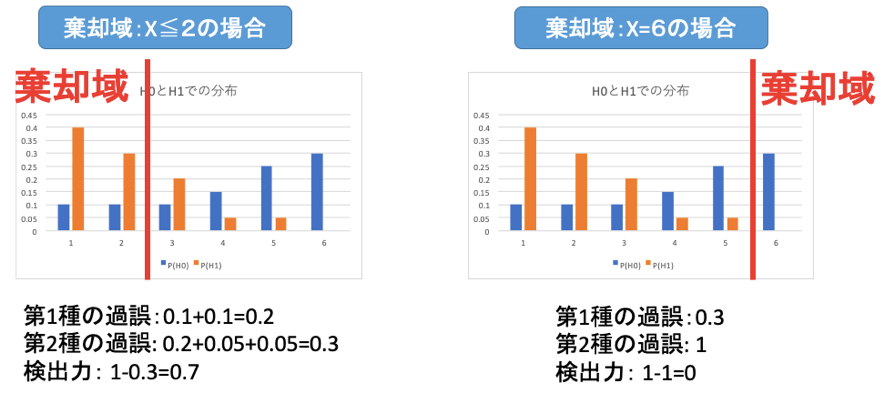
統計検定2級2018年6月の過去問解説!問13(2)
X≦2が棄却域の場合と、X=6が棄却域の場合、第1種の過誤、第2種の過誤、検出力はそれぞれ以下の通り。
有意水準とは、第1種の過誤とほぼ同じ意味です。
統計検定2級2018年6月の過去問解説!問14(1)
回帰分析の読み取り方です。
問題文で与えられた回帰式に、出力結果を当てはめると以下の式になります。
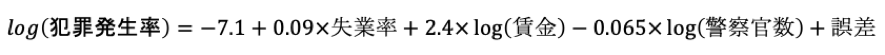
ここに、問題文の数字を当てはめます。

統計検定2級2018年6月の過去問解説!問14(2)
回帰分析の結果から、t統計量を求める式は以下の通り。

よって、値を代入するとこのようになる。
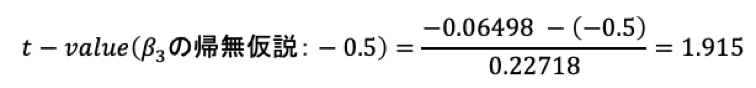
計算結果のt統計量を、t分布表と見比べる。
自由度は回帰分析結果のResidual Standard Errorを見る。
43degree of freedomとあるため、自由度40のt分布表を確認する。
すると、得られたt=1.915は両側10%と両側5%の間のt値に相当する。
そのため、両側10%であれば棄却される。
統計検定2級2018年6月の過去問解説!問14(3)
I:◯
Interceptとlog(賃金)の2つが有意水準1%で0ではない。
II:×
Log(賃金)の推定値は正の値であり、有意水準1%で0ではない。
そのため、賃金が上がると犯罪発生率は上がる傾向にある。
III:◯
自由度調整済み決定係数は、回帰分析結果のAdjusted R-squaredの値である。
統計検定2級2018年6月の過去問解説!問15(1)
分割表の基本的な知識を問う問題。
与えられた表から期待度数の表を作成すると、以下のようになります。

統計検定2級2018年6月の過去問解説!問15(2)

よって、数字を代入すると以下の通り。
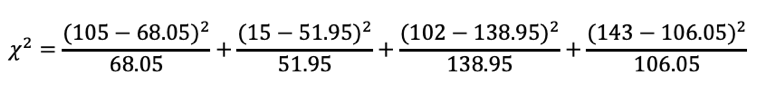
統計検定2級2018年6月の過去問解説!問15(3)
分割表の自由度は、(行の数-1)*(列の数-1)で計算できる。
よって、2*2分割表の場合の自由度は1である。
カイ二乗分布表より、自由度1のときに0.05となるカイ二乗値は3.84

また、(2)より計算されたカイ二乗値は69.04である。
69.04>3.84であるため、風向と季節には関連があると言える。
統計検定2級2018年6月の過去問解説!問16
F値の求め方は、以下の通り。
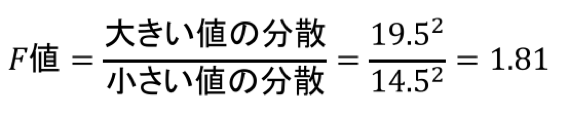
また、自由度(20, 40)の両側5%のF統計量は下記の通り2.068となる。
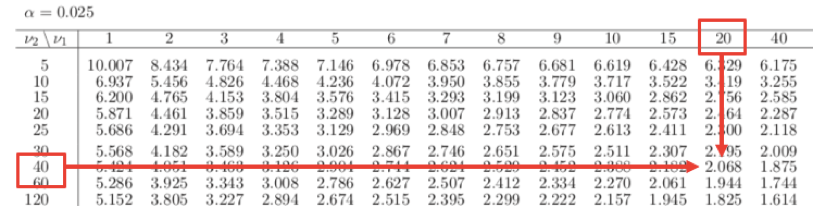
1.81<2.068であるため、棄却されない。











コメント
コメント一覧 (5件)
統計が変わりません
コメントありがとうございます。
ぜひ、本サイトとメールセミナーを通じて統計を学んでみてください。
[…] 2018年6月に実施された統計検定2級の過去問の解説もしています。 […]
[…] 2018年6月に実施された統計検定2級の過去問の解説もしています。 […]
統計検定2級合格を目指しています。
公式テキストの解説では理解し辛い部分について、分かりやすく説明されており学習の参考させて頂いています。
ありがとうございます。