偏相関係数は、医療統計でたまに見かける単語。
相関係数の説明はほとんどの統計の書籍にあります。
しかし偏相関係数について説明している書籍は意外と少ないです。（中級者以上向けの本なら紹介されています）
そのため
「偏相関係数って相関係数と何が違うの？」
「偏相関係数をわかりやすく説明してほしい！」
といった方も多いのではないでしょうか。
本記事では偏相関係数の意味や導出、活用法についてわかりやすく解説していきます。
偏相関係数を理解するには疑似相関に関する理解も必要。
ぜひ偏相関係数を使いこなせるようになっていってくださいね！
Contents
偏相関係数とは何でどんな意味？疑似相関についてもわかりやすく解説！
偏相関係数の理解のためには、いわゆる疑似相関というものを理解する必要があります。
偏相関係数とは？疑似相関とは？
偏相関係数とは、”指定した変数の影響をなくした状態で”2つの変数間がどのように相関するか表す指標です。
2つの変数間だけで計算する相関係数と違い、他の変数の影響まで考慮している点が違います。
簡単な例を挙げてわかりやすく説明していきますね。
1日の運動量と血圧の関係を検証することにしましょう。
理想は「運動量と血圧が関係するから運動は大事です」という発表にすることだと考えています。
そこで運動量と血圧の相関係数を算出したところ、両者に高い相関を認めました。
じゃあ早速学会発表！といきたいところですがちょっと待ってください。
ここで出た相関は実は疑似相関かもしれません。
疑似相関とは第3の変数が影響して、本来相関のないもの同士が見かけ上相関してしまっている状態のことです。
今回の場合、”年齢”が第3の変数にあたります。
年齢は運動量と血圧どちらにも相関するため、疑似相関を引き起こす可能性があります。
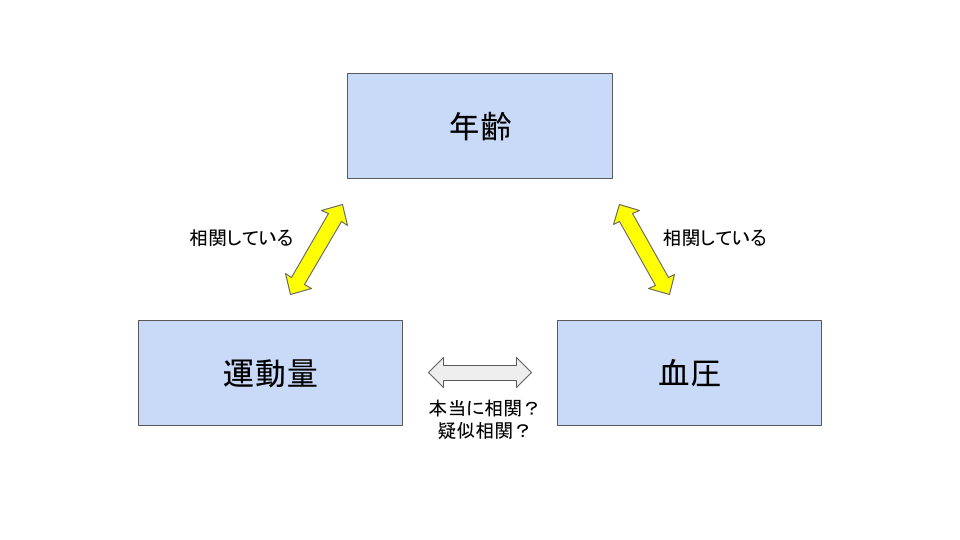
このままでは「運動量が少ない人は高齢者が多いから血圧と相関しただけじゃないの？」なんてツッコミをされかねません。
学会で運動量と血圧の相関を主張したいなら疑似相関ではないこと示しておきたいところです。
そこで役に立つのが偏相関係数です。
偏相関係数を算出することで、”年齢”の影響をなくした状態で”運動量”と”血圧”がどのように相関するか検証することができます。
第三の因子の影響を除いた関係を見る点では、共分散分析などの多変量解析と似ていますね。
偏相関係数は因果関係を示すわけではない
偏相関係数はあくまで相関係数ですので、因果関係を示すわけではありません。
これはよくある間違いですので注意してください。
どういうことでしょうか？
先ほどの例の続きを使って説明しますね。
“年齢”の影響をなくして(正しくは”年齢で調整をかける”と表現します)偏相関係数を算出してみました。
すると偏相関係数でも”運動量”と”血圧”は高い相関を示していたとします。
これで年齢とは関係なく両者が相関していることが示されました。
ただしここで発表の際に「運動量は血圧に影響を与えます」と言ってしまってはいけません。
なぜなら”血圧”が運動量に影響を与えているかもしれないからです。
血圧が高くて体がしんどいので運動量が少なくなってしまっている可能性もありますよね。
これが真実だった場合、運動量をあげたところで血圧が改善するとは限りません。
このように「運動量→血圧」なのか「血圧→運動量」なのか、偏相関係数では知ることはできません。
学会発表では「運動量と血圧に相関を認めた」というところまでしか言うことはできません。
実際によくあるミスですので、偏相関係数の解釈には注意してくださいね！
偏相関係数と偏回帰係数の違い：偏相関係数は1以上や-1以下にはならない
偏相関係数と似た言葉で、偏回帰係数というものがあります。
これらは何が違うのでしょうか？
最大の違いは、算出する目的です。
偏相関係数は-1~1の間で相関を示すため先ほどの例のように変数間の相関の程度を知りたい時に有効です。
偏回帰係数は重回帰分析である変数がどれくらい目的変数を説明しているか知りたい時に使います。
偏回帰係数は-1以下にも1以上にもなるため、その値だけではどれくらい相関しているのか分からない点が偏相関係数と異なります。
どちらも他の変数の影響をなくした上で相関関係を算出している点は同じなのですが、相関の強さをみるなら偏相関係数のほうが有効です。
偏相関係数の導出法
偏相関係数の計算式
ここからは偏相関係数はどのように他の変数の影響をなくした状態にしているのか、説明していきますね。
まず偏相関係数の計算式はこのようになっています。
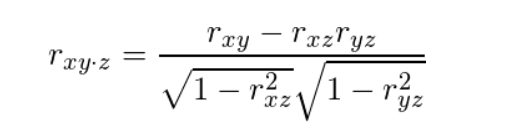
変数zで調整して変数xと変数yの偏相関係数を求めています。
これを見て「なるほど！そういうことか！」となった方、いますかね？
数学がよっぽど得意じゃないと意味不明だと思います。。。
でも安心してください！
一体全体なんでこんな数式になるのか、日本語でわかりやすく説明していきますね！
偏相関係数は残差の相関係数
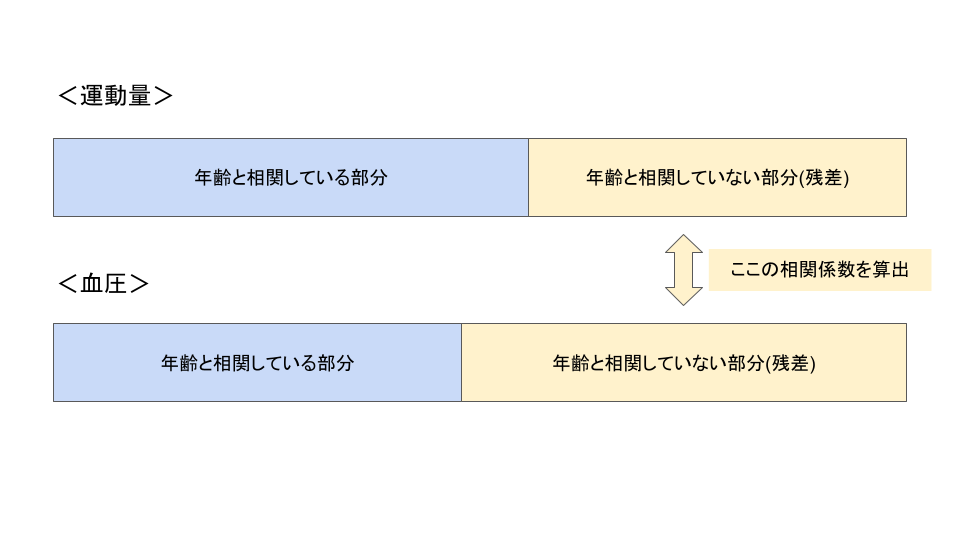
実は偏相関係数とは、変数と調整する変数の残差をそれぞれ使って相関係数を算出しただけなんです。
もう少しわかりやすく説明しますね。
ある変数とある変数が相関する場合、相関係数が1や-1でなければ必ず相関する部分と相関していない部分に分かれます。
この変数間で相関していない部分のことを”残差”といいます。
ここまで大丈夫でしょうか？
ここからは先ほどの例を使って、運動量と血圧の偏相関係数を年齢で調整して算出する場合を考えていきましょう。
偏相関係数を算出するまでの流れは以下のようになります。
- 運動量と年齢の残差を算出
- 血圧と年齢の残差を算出
- 残差同士の相関係数を算出
いかがでしょうか？
それぞれの残差は年齢と相関していない部分ですから、これら残差の相関を見れば年齢の影響をなくした関係が分かるよ！ということです。
今の流れを数式を使って計算してまとめると最初にお見せした計算式になります。
偏相関係数には相関係数みたいな目安はある？
偏相関係数の相関の強さを決める目安は相関係数と同じです。
ただし第3の変数で調整をした後の相関の強さですので、解釈には注意が必要です。
相関係数の値の目安は様々ですが、一般的には以下のようになります。
- 相関係数の絶対値が0.2以下：ほぼ相関していない
- 相関係数の絶対値が0.2~0.4：弱い相関
- 相関係数の絶対値が0.4~0.6：中等度の相関
- 相関係数の絶対値が0.6~0.8：強い相関
- 相関係数の絶対値が0.8以上：非常に強い相関
まとめ
最後におさらいをしましょう。
- 偏相関係数とは”指定した変数の影響をなくした状態で”2つの変数間がどのように相関するか表す指標
- 偏相関係数は偏回帰係数と比べた時に相関が強さを解釈しやすい点で異なる
- 偏相関係数は調整する変数との残差を使って相関係数を算出したもの
- 偏相関係数の値の目安は相関係数と同じ
後方視的研究をする場合、複数の変数同士で影響を及ぼし合うため結果の解釈に困ることがよくあります。
この時いきなり重回帰分析などの多変量解析をかけてしまうこともありますが、重回帰分析では目的変数と各説明変数の関係性しか分かりません。
重回帰分析をかける前に偏相関係数を各変数間で算出しておくと、結果の解釈がしやすくなります。
使ってみると分かるのですが、偏相関係数は非常に便利です。
今まで使ったことのない方はぜひ使ってみてくださいね！
最後までお読みいただきありがとうございました。
第1章：臨床研究ではなぜ統計が必要なのか？計画することの重要性
第2章：研究目的をどれだけ明確にできるのかが重要
第3章：p値で結果が左右される時代は終わりました
第4章：多くの人が統計を苦手にする理由
第5章：統計を使えるようになるために今日から何をすれば良いか？
第6章：統計を学ぶために重要な環境
もしあなたがこれまでに、何とか統計をマスターしようと散々苦労し、何冊もの統計の本を読み、セミナーに参加してみたのに、それでも統計が苦手なら…
私からプレゼントする内容は、あなたがずっと待ちわびていたものです。
