この記事では「標準偏回帰係数(標準化回帰係数)とは?Rでの実施方法も解説!」ということでお伝えします。
- そもそも標準化とは?
- 回帰分析で偏回帰係数の弱点と標準変回帰係数を求める目的
- Rで標準変回帰係数を求める
ということを理解できるようになります!!
そもそも標準化とは?
標準化回帰係数(標準偏回帰係数)を理解するために、まずは「標準化」ということをまずは理解しましょう。
「標準化」が出てくる場面としては、標準正規分布を考える時です。
標準正規分布とは、平均0、標準偏差1の正規分布のこと。
統計で言う「標準化」とは、上記のような平均0、標準偏差1の正規分布に変換することを言います。
具体的には、下記のような変換を実施します。
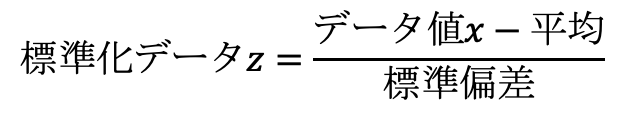
標準化をするメリットは「単位がなくなるので異なるデータでも比較が可能になる」という点。
例えば、体重と身長のデータを比較できたり、日本円とアメリカドルのデータを比較できたりすることができます。
回帰分析での(標準化されていない)偏回帰係数の弱点
標準化がわかったところで、ではそもそも標準化されていない偏回帰係数にはどんな弱点があるのでしょうか?
重回帰分析、ロジスティック回帰分析、Cox比例ハザードモデルなど、多変量解析を実施すれば必ず出てくる偏回帰係数。
偏回帰係数とは、xが1単位(例えば体重なら1kgあたり)変化するごとのyの変化度合いを示しています。
弱点は、説明変数の単位が異なると異なる値を示すため、 目的変数の影響度の大きさを説明変数同士で比較したい場合には使いにくい、ということ。
そのため、説明変数の影響度の大きさを比較するために、標準偏回帰係数を求めることがあるんです。
標準偏回帰係数を求める目的
標準化に関する理解と、標準化していない偏回帰係数の弱点を整理できると、標準偏回帰係数を求める目的が見えてきました。
標準偏回帰係数を求める目的は、ただ一つです。
説明変数間の目的変数に対する影響度の大きさを比較するため
上記が、標準変回帰係数を求める目的です。
Rで標準偏回帰係数を求める方法
標準偏回帰係数に関して整理できたので、実際にRで標準変回帰係数を求めてみましょう。
ゴール設定は、SAS社のこちらのページにある下記の結果を再現することです。(ただし、切片は再現できない。)
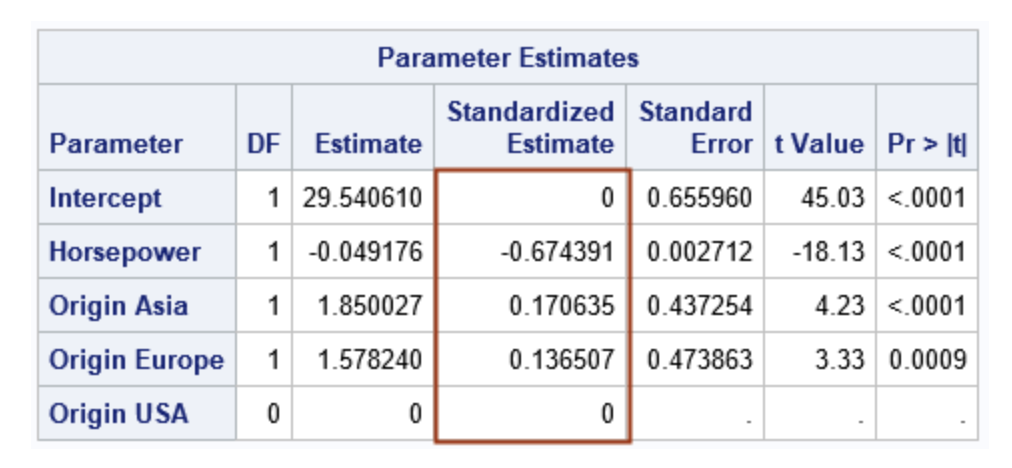
このプログラムに用いるデータはこちらからダウンロードできますので、ぜひ実際にやってみてください。
実際のRプログラム
では、実際のRプログラムです。すでにデータが「cars_sas」という名前でRの中にインポートしている前提でのプログラムであることをご注意ください。
# carsデータセットを読み込む
head(cars_sas)
str(cars_sas)
# まずは標準化しない線形回帰モデルを作成
model <- lm(MPG_City ~ Horsepower + Origin, data = cars_sas)
summary(model)
# Origin列をダミー変数化
dummy_cars <- model.matrix(~ Origin - 1, data = cars_sas)
cars2 <- data.frame(cars_sas,dummy_cars)
# 変数を標準化する関数
standardize <- function(x) {
(x - mean(x)) / sd(x)
}
# 説明変数と目的変数を標準化
cars_std <- data.frame(
MPG_City = standardize(cars2$MPG_City),
Horsepower = standardize(cars2$Horsepower),
Origin_Asia = standardize(cars2$OriginAsia),
Origin_Europe <- standardize(cars2$OriginEurope)
)
# 標準化したデータで線形回帰モデルを実施
model_std <- lm(MPG_City ~ Horsepower + Origin_Asia + Origin_Europe, data = cars_std)
summary(model_std)# carsデータセットを読み込む
head(cars_sas)
str(cars_sas)
# まずは標準化しない線形回帰モデルを作成
model <- lm(MPG_City ~ Horsepower + Origin, data = cars_sas)
summary(model)
# Origin列をダミー変数化
dummy_cars <- model.matrix(~ Origin - 1, data = cars_sas)
cars2 <- data.frame(cars_sas,dummy_cars)
# 変数を標準化する関数
standardize <- function(x) {
(x - mean(x)) / sd(x)
}
# 説明変数と目的変数を標準化
cars_std <- data.frame(
MPG_City = standardize(cars2$MPG_City),
Horsepower = standardize(cars2$Horsepower),
Origin_Asia = standardize(cars2$OriginAsia),
Origin_Europe <- standardize(cars2$OriginEurope)
)
# 標準化したデータで線形回帰モデルを実施
model_std <- lm(MPG_City ~ Horsepower + Origin_Asia + Origin_Europe, data = cars_std)
summary(model_std)上記のプログラムを実行すると、下記のような結果が出力されます。
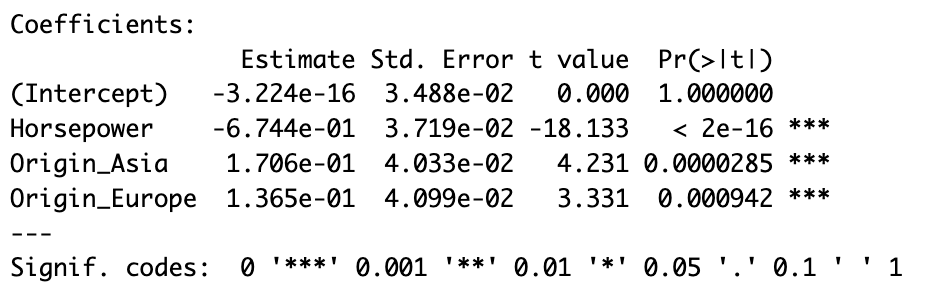
こちらをSASの結果と再度見比べてみます。(e-01は10のマイナス1乗の意味です。)
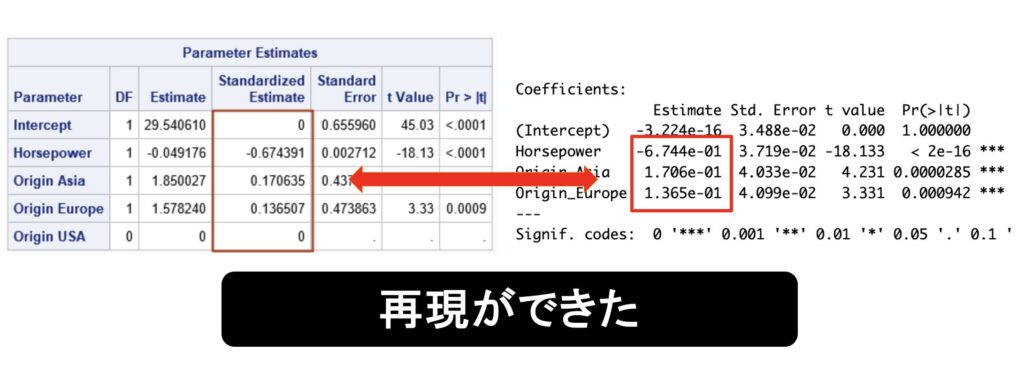
e-01は10のマイナス1乗の意味なので、再現ができました。
標準偏回帰係数を求める際の議論
標準変回帰係数を求める際に議論となっていることがあります。
それは、「因子型のデータ(カテゴリカルデータ)を標準化する必要はあるのか?」ということ。
因子型変数は通常、ダミー変数(0と1のコーディング)に変換されて回帰分析に使用されます。
そして、ダミー変数は既に0と1の値を持っているため、さらに標準化する意味がないのでは、という議論です。
例えば、性別(男性=0、女性=1)の係数が2.5の場合、 他の変数が一定の条件下で、女性は男性よりも平均して 2.5単位高い値を持つことを意味しており、因子型変数に関しては、上記の解釈が全て。
そのため、わざわざ標準化する意味がなく、標準化すると解釈が難しくなる可能性があります。
ただ、今回の記事ではSASでの数値を再現するためにダミー変数も標準化しました。
臨床研究では説明変数が1単位変化した場合の目的変数の変化を解釈することに興味があることが多いため、 標準化しない偏回帰係数を求めることがほとんどかなと思います。
まとめ
いかがでしたか?
この記事では「標準偏回帰係数(標準化回帰係数)とは?Rでの実施方法も解説!」ということでお伝えしました。
- そもそも標準化とは?
- 回帰分析で偏回帰係数の弱点と標準変回帰係数を求める目的
- Rで標準変回帰係数を求める
ということを理解できたのなら幸いです!
この記事の内容は、動画でもお伝えしていますので併せてご確認くださいませ。














コメント