医療統計やデータ解析の現場で必ずといっていいほど登場する「等分散(とうぶんさん)」という概念。t検定を行う際に「分散が等しいかどうかを確認しなさい」と教わり、F検定を行っている方も多いでしょう。
しかし、現代の統計実務においては、この「等分散の検定(F検定)」をステップに挟む手法は、むしろ推奨されないことが一般的です 。
本記事では、統計学の専門書に基づき、等分散の定義から「なぜF検定が不要なのか」という深い理由、そして実務で最も信頼できる解析手法の選び方まで、詳細な解説を提供します。
等分散と不等分散の基礎知識
統計学的検定を適切に選択するためには、まずデータのばらつき(分散)の性質を正しく理解する必要があります。
等分散・不等分散とは何か?
等分散(homoscedasticity)とは、比較しようとする異なるグループ間でデータのばらつき(分散)が等しいことを指します 。例えば、新薬群とプラセボ群で血圧の低下量を比較する場合、両群のデータの広がり方が同程度であれば「等分散」です。
一方で、グループ間でデータのばらつきが明らかに異なる状態を「不等分散(heteroscedasticity)」と呼びます 。
なぜ統計検定で「等分散」が問題になるのか
最も有名な統計手法の一つである「スチューデントのt検定」は、パラメトリック検定に分類されます。パラメトリック検定とは、データが特定の確率分布(一般的には正規分布)に従っていると仮定して解析を行う手法です 。
スチューデントのt検定には、以下の2つの大きな前提条件があります 。
- 各群のデータが正規分布であること
- 群間でばらつきが等分散であること
もしデータが不等分散であるにもかかわらずスチューデントのt検定を強行すると、算出されるP値の正確性が失われ、誤った結論を導き出すリスクが生じます 。そのため、従来は「まずF検定で等分散性を確かめる」というプロセスが必須だと考えられてきました。
【重要】なぜ等分散の確認に「F検定」は推奨されないのか?
多くの教科書で紹介されている「F検定を行ってから、t検定の手法(スチューデントかウェルチか)を決める」という2段階検定。しかし、実務においてこの手順は強く推奨されていません 。その決定的な理由は、以下の3点に集約されます。
① 検定では「等しい」ことを証明できない
統計学的検定の根本的なルールとして、「等しい(差がない)」ことを直接証明することはできません 。
F検定において、P値が有意水準(0.05)を上回ったとしても、それは「分散が異なるとは言えなかった」という消極的な結論にすぎず、「分散が等しい」という証拠にはならないのです 。
② 検定結果がサンプルサイズに依存しすぎる
F検定の結果は、データの数(サンプルサイズ:n数)に大きく左右されます 。
- サンプルサイズが大きい場合: 臨床的に全く意味のない微小な分散の差であっても、P値が0.05を下回り「不等分散」と判定されてしまいます 。
- サンプルサイズが小さい場合: 明らかに分散が異なっていても、統計的な検出力が不足しているために「等分散(有意差なし)」と判定されるミスが起こりやすくなります 。
このように、症例数設計がなされていない等分散検定の結果は、信頼性が非常に低いのです 。
③ 検定の多重性によるエラーの増大
F検定を行った後にt検定を行うのは、一つの研究の中で2回検定を繰り返す「2段階検定」です。これにより、統計学的な「多重性の問題」が発生します 。
最初のF検定ですでに間違える可能性(αエラー)を含んでいるため、その後のt検定を合わせた最終的な結果は、本来設定した有意水準(0.05など)を超える高い確率で間違いを犯してしまうことになります 。
実務で推奨される「等分散性」の判断と対処ルール
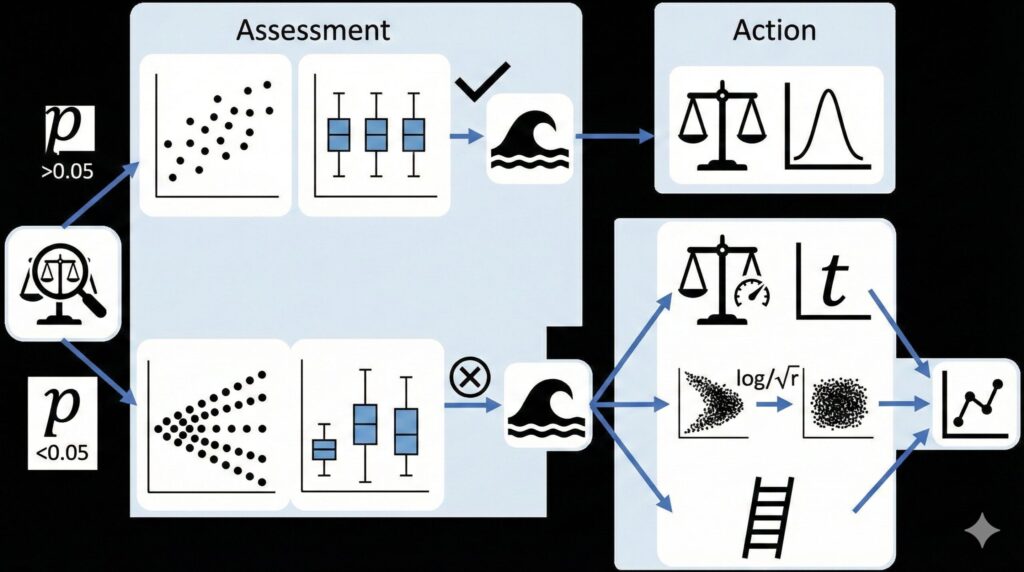
F検定を使わずに、どのようにデータの性質を判断し、適切な解析手法を選べばよいのでしょうか。推奨される実務的なルールを解説します。
データの可視化と要約統計量の確認
検定に頼る前に、まずは自分の目でデータのばらつきを確認することが大原則です。
- ヒストグラムや箱ひげ図を作成する: グラフを見て、左右の広がり方が大きく異ならないか視覚的にチェックします 。
- 不偏分散の比を確認する: 統計ソフトで出力された分散の比を計算します。一つの目安として、「分散の比が1.5倍以下」であれば、等分散とみなしてスチューデントのt検定を用いても良いとする見解もあります 。
推奨される最強の解決策:常に「ウェルチのt検定」を選ぶ
等分散か不等分散かで悩む時間をなくし、最も正確な結果を得るための最適解は、「最初から等分散を仮定しない、ウェルチのt検定を常に選択すること」です 。
ウェルチのt検定には、実務上非常に優れた以下のメリットがあります。
- 汎用性が高い: 等分散であっても不等分散であっても、どちらの状況でも適用可能です 。
- 検出力のバランスが良い: 分散が実際に等しい場合にはスチューデントのt検定に比べて検出力がわずかに低下しますが、分散が異なる場合にはむしろ検出力が増加するという研究結果があります 。
つまり、迷うくらいであれば、最初からウェルチのt検定を実施することが、統計的なエラーを最小限に抑えるための知恵と言えます 。
解析ソフト「R」での実践:等分散性の確認から検定まで
実際に統計解析ソフト「R」を用いて、どのように等分散性を評価し、検定を使い分けるのか。書籍にある手順を参考にシミュレーションします。
ステップ1:ヒストグラムによる視覚的確認
ggplot2パッケージを使用し、各群の分布とばらつきを確認します。
# 2群のヒストグラムを作成(例:アヤメのデータを使用)
library(ggplot2)
ggplot(iris_new, aes(x = Sepal.Length, fill = Species)) +
geom_histogram(position = "identity", alpha = 0.8) +
theme_minimal()
これにより、例えば「setosa群よりもversicolor群の方がばらつきが大きそうだ」といった洞察を事前に得ることができます 。
ステップ2:要約統計量の算出
dplyrパッケージを使い、各群の「分散(Var)」を数値化します。
library(dplyr)
summary_stats <- iris_new %>%
group_by(Species) %>%
summarise(var = sd(Sepal.Length)^2)
ここで算出された分散の比が1.5倍を超えている場合、より慎重な手法(ウェルチのt検定)の選択が妥当だと判断できます 。
ステップ3:検定の実施(ウェルチのt検定)
Rのt.test()関数は、デフォルト設定(var.equal = FALSE)でウェルチのt検定が実行されるようになっています 。
# ウェルチのt検定を実行
t.test(setosa$Sepal.Length, versicolor$Sepal.Length)
出力結果の「Welch Two Sample t-test」という表記を確認し、得られたP値、点推定値、95%信頼区間の3点セットを報告します 。
まとめ:等分散の呪縛から解き放たれるために
本記事の要点をまとめます。
- 等分散は「グループ間でのデータのばらつきが等しいこと」を意味する 。
- 従来のF検定(等分散の検定)は、等しいことを証明できず、多重性の問題を引き起こすため、実務では非推奨である 。
- 実務的な解決策は、最初から等分散を仮定しない「ウェルチのt検定」を常に選択することである 。
- 判断に迷う場合は、箱ひげ図などのグラフで視覚的にデータを確認し、理論的な裏付け(先行研究など)をもって手法を決定する 。
統計解析の真の目的は、研究目的に対して最適な「解釈」を下すことです。P値の大小に一喜一憂する(p-hacking)のではなく、データの取得方法や背景情報を考慮し、透明性の高い解析を心がけましょう 。
>>ウィルコクソンの順位和検定とは?マンホイットニーのU検定との違いは?











コメント