F検定とは？わかりやすくF分布のグラフからP値の読み取り方まで

データの分散が等しいかどうかを検定する時に用いるF検定。

F検定は、T検定の前に、等分散かどうかを確かめるときによく用います。

ではF検定はどのようなことが行われているのでしょうか?

また、T検定との関係はどういったものなのでしょうか?

この記事ではF検定について、わかりやすく説明していきます。

F検定とは?わかりやすく説明するとどんな検定？

F検定とは、ズバリ、”分散が等しい”かどうかを調べる検定です。

”分散”は、データのばらつきを示す指標ですよね。

なぜばらつきが等しいかどうかを調べなきゃいけないの？

どんな時に分散を調べる必要があるの？

というのが疑問です。

F検定とT検定との関係

F検定がもっともよく使われるのは、間違いなくT検定のとき。

T検定では、比較する群が等分散か、等分散ではないかで、統計の手法が変わってきます。

• 比較する群が等分散（分散が等しい）のときは、スチューデントのT検定、
• 等分散ではないときはウェルチのT検定を用います。

そのため、等分散か、等分散ではないか、を調べるときにF検定を使います。

しかし、T検定前に等分散かどうかの検定を行うとは正しくないという意見もあり、今ではF検定を行わずに、等分散の仮定が不要な、ウェルチのT検定を用いたりします。

>>T検定とは？帰無仮説と対立仮説を必ず確認！F検定で等分散の確認が必要？

（ちなみに私はF検定使用しない方がいい派です。）

では、F検定ってどういうときに使うのでしょうか?

F検定はいつ使われるのか?

F検定はT検定のときは、あまり使われなくなりました。

しかし、それでもF検定はたくさん使われています。

それは、「分散分析: ANOVA (analysis of variance)」です。

２つのグループの平均の違いを調べるのがT検定でしたが、

分散分析では3つ以上のグループのときに、用いる方法です。

>>>分散分析とは？分散分析表の見方やf値とp値の意味もわかりやすく！　

では、F検定が実際にどのようなものかをみていきましょう。

F検定を知る上で重要なF分布をわかりやすく！

F検定を説明するうえで欠かせないのがF分布です。

F分布の式はややこしいのでここでは説明しませんが、ここでは、F分布はどんなものかを説明します。

ちなみにF分布はこういう形をしています。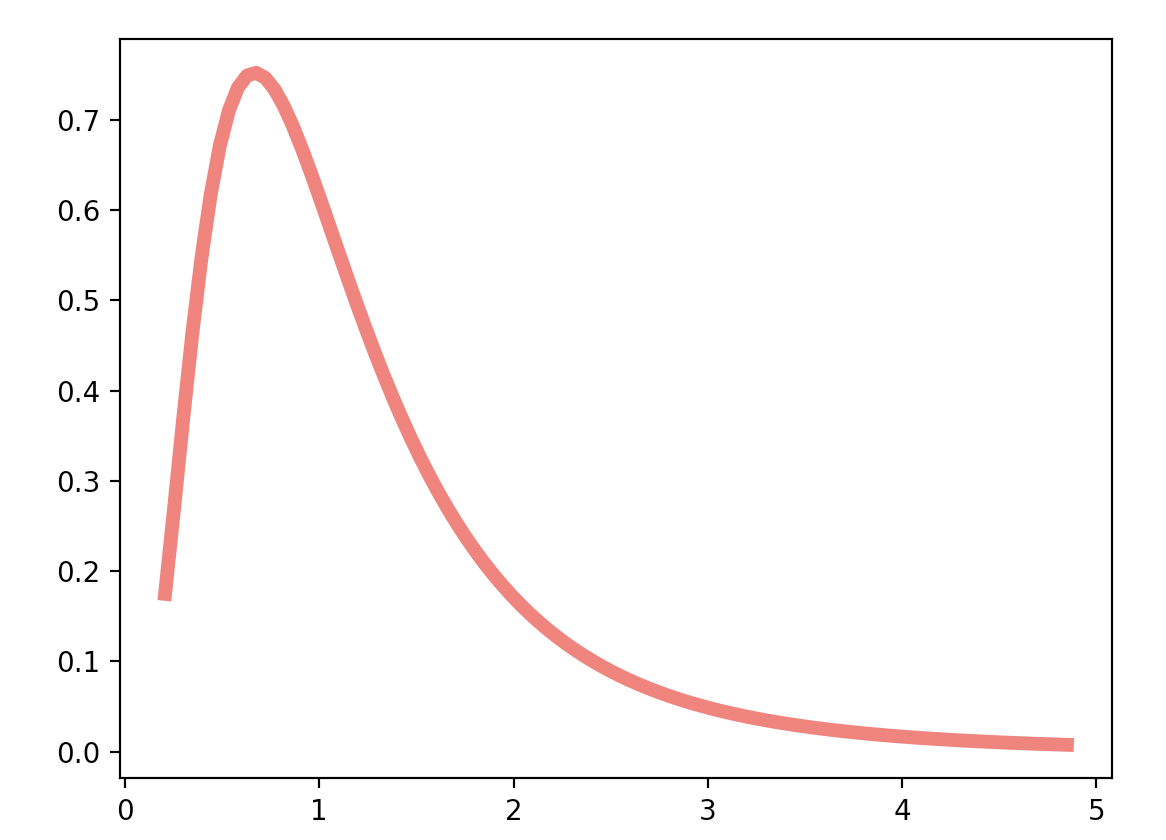

F分布の特徴は、正規分布とは異なり、左右対称ではないことです。

あた、この分布の形は２つの自由度から求めることができますが、自由度については後ほど説明します。

もう一点重要なこととして、F分布を説明するにはカイ二乗分布がかかせません。

どういうことかと言いますと、次のような法則あるからです。

標準正規分布に従う独立なn個の変数がありこれらをu₁、u₂、・・・u_nとします。

>>>標準正規分布表の見方について！標準化やZ値の計算式はどうすればいい？

このとき、u₁、u₂、・・・u_nの変数の2乗和は、

x=u₁²+u₂²+・・・+u_n²

と表すことができます。

このときのxは自由度nのカイ二乗分布に従う。

このxは分散をnで割っていないだけの値ですよね。

これは、一つの分布についての法則です。

F分布は2つの分布を比べるときに出てくる法則です。

自由度k₁のカイ二乗分布に従う変数をu₁ 、自由度k₂のカイ二乗分布に従う変数をu₂、のカイ二乗値の比

$$F = \frac{\chi^2_1 / k_1}{\chi^2_2 / k_2} = \frac{\chi^2_1 / (n_1 – 1)}{\chi^2_2 / (n_2 – 1)} = \frac{\frac{(n_1 – 1)s_1^2}{\sigma_1^2} / (n_1 – 1)}{\frac{(n_2 – 1)s_2^2}{\sigma_2^2} / (n_2 – 1)} = \frac{s_1^2 / \sigma_1^2}{s_2^2 / \sigma_2^2}$$

はF分布に従う。

要するに、分散の比がF分布に従うということ。

F分布はこの法則にしたがっており、F検定ではF分布を用いて検定を行います。

また、F検定は通常、データが正規分布をしていることが前提なのも注意が必要です。

そのため、近年は正規分布に従わなくても使える検定法も考案されています。

F検定における自由度とは？

ここで自由度が出てきたので、説明しましょう。

カイ二乗検定における自由度に関しては、こちらの記事をご参照ください。

自由度とは、変数のうち独立に選べるものの数のことをいいます。

ここでは例として、三角形の内角の和を考えます。

角A、B、Cからなる三角形の内角の和は180°です。

このとき、三角形の自由度は2です。

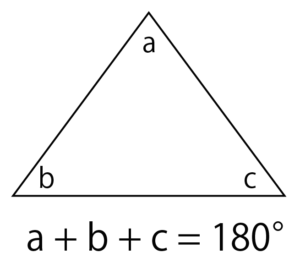
理由は、自由に決めれる内角は2つしかないからです。

例えば、角Aを60°と決めたとします。

このとき、BとCの合計が120°になれば、あとはBとCの内角は自由に決めることができます。

次にBを30°と決めたとします。

すると、Cは90°と決まってしまします。

角Aと角Bの２つは自由に決められたが、AとB が決まるとCが勝手に決まるので、

このときは自由度2といいます。

カイ二乗分布やF分布では、何個の確率変数をとれるかが、自由度に対応しています。

通常、自由度は標本のデータ数から1を引いた値を用います。

F検定の帰無仮説と対立仮説：P値が有意になったらどんな結論？

それでは、F検定について考えていきます。

F検定では次のような帰無仮説と対立仮説を立てます。

• 帰無仮説：2グループの分散に差がない
• 対立仮説：2グループの分散に差がある

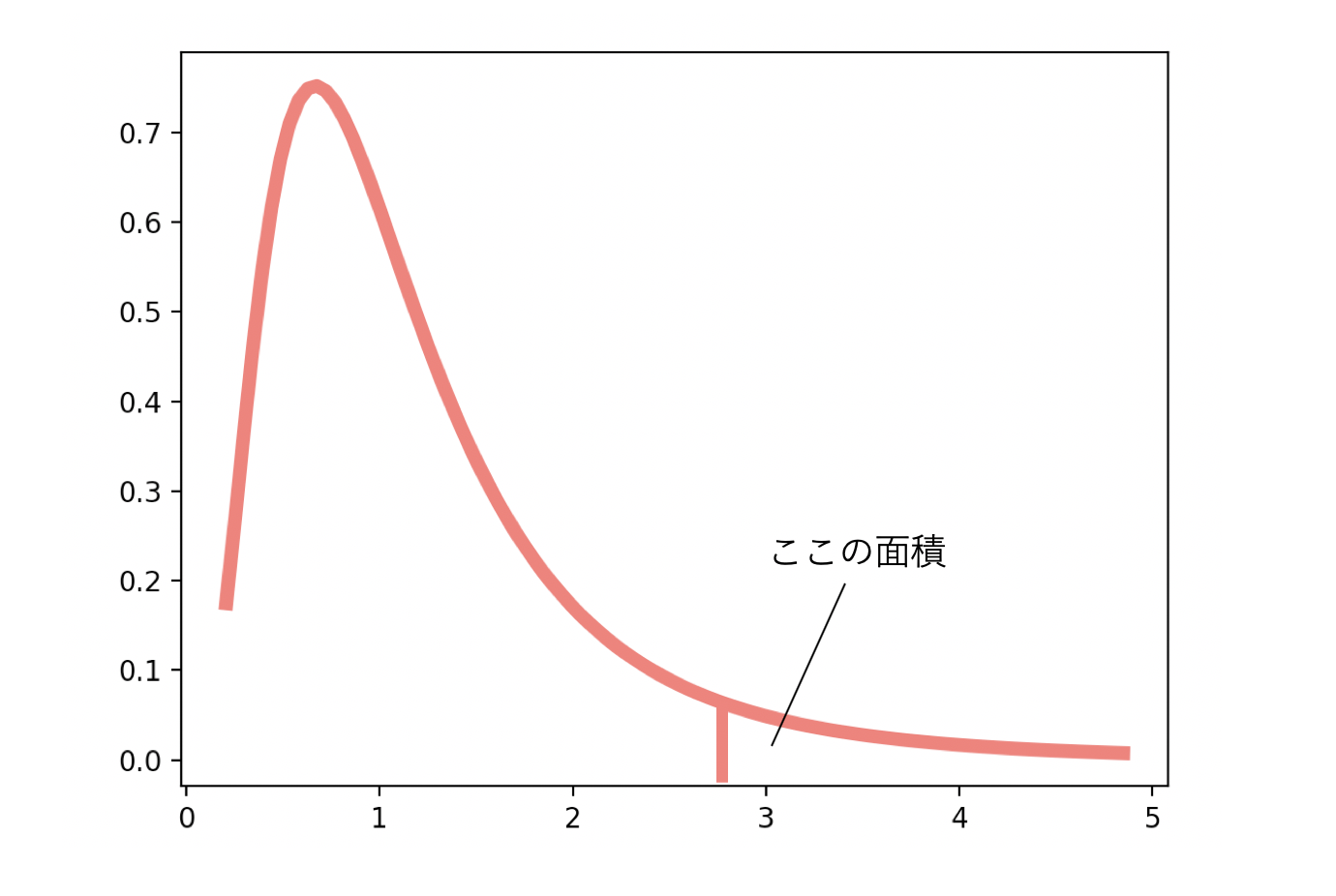
有意水準が0.05であれば、

上の図の面積が0.05以下のときに、帰無仮説が棄却されることになり、2つのグループの分散には差があると結論づけられます。

F分布表では、二つの自由度から、面積が0.05になる横軸の値が書かれています。

二つの自由度はそれぞれの標本のデータ数から1を引いた値を用います。

そのため、その値よりも横軸が大きければ、有意に分散が違うということができます。

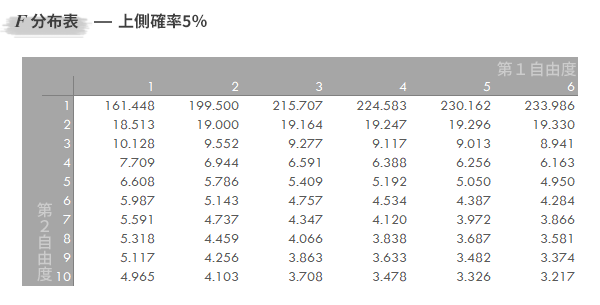
ちなみに上の図では、自由度が10と10になるため、有意になる横軸の値は2.98です。

F検定をわかりやすく！まとめ

ここでは、F検定について見ていきました。

F検定は分散の違いに関する検定で、T検定を実施する前に使われることが多いです。

しかし、どのT検定を使うのかという判断に対してF検定を使うことには議論があって、私自身はF検定は不要だと思っております。

F検定は二つの自由度を用いて行います。