MENU
数式にとらわれない、イメージとしての統計！
  1. ホーム
  2. 個々の統計検定の説明
  3. 対応のあるデータ・対応のないデータとは？例を用いてわかりやすく解説！

対応のあるデータ・対応のないデータとは？例を用いてわかりやすく解説！

個々の統計検定の説明
対応のあるデータ・対応のないデータとは？例を用いてわかりやすく解説！

この記事では「対応のあるデータ・対応のないデータとは？例を用いてわかりやすく解説！」ということでお伝えしていきます。

  • 対応のあるデータとは？対応のないデータとは？違いって何？
  • 対応のあるt検定と対応のないt検定をわかりやすく解説
  • その他の対応のある検定

これらのことがわかるようになりますので、ぜひ最後まで見ていってくださいね！

＞＞もう統計で悩むのは終わりにしませんか？ 

↑期間・数量限定で無料プレゼント中！

目次

対応のあるデータとは？対応のないデータとは？例を用いて解説

まずは対応のあるデータと、対応のないデータがどんなものなのかを整理していきましょう。

対応のあるデータとは？

対応のあるデータを一言で言うと「同一のサンプルから得られているデータ」ということ。

例えば、今日のある豚さんの値と、一週間後の同じ豚さんの値を比較したい時。

この場合、サンプルとしては同一ですが、時点だけ異なるデータになります。

同一サンプル（被験者）から複数の条件または時点で得られるデータを、対応のあるデータと呼んでいるのです。

対応のあるデータの例

A群のベースラインの血圧と、A群の2週間後の血圧

上記の例は、臨床研究でもよくありますよね。

「A群」という同じグループ（サンプル）のデータを比較するため、対応のあるデータになります。

対応のあるデータは同一被験者から複数のデータが得られるため、データ間には強い相関関係があります。

対応のあるデータの分析では、通常、差の分析や対の比較が行われます。

これにより、同一被験者の条件変化による効果を直接評価することができるため、より精度の高い結果を得ることが可能。

対応のないデータとは？

では一方で、対応のないデータとはどんなデータでしょうか？

それは「異なるサンプルから得られているデータ」です。

時点は同じでもよく、とにかく異なるサンプルから取られているデータを比較したい時には、対応のないデータの比較をする、ということになります。

対応のないデータの例

A群のベースラインの血圧と、B群のベースラインの血圧

これも臨床研究でよくある状況ですよね。

「A群」と「B群」という違うグループのデータを比較するため、対応のないデータの比較になるのです。

対応のないデータでは異なるグループ間の比較に集中するため、例えば治療群と対照群の間での平均の違いを分析することが一般的です。

対応ありなしでt検定は変わる？わかりやすく解説

対応のあるデータや対応のないデータを調べていくと、t検定についての記載が多いことに気付きます。

「もしかしてt検定っていろんな種類があるのかな？」と勘違いしてしまうほど。

  1. 1群のt検定
  2. 対応のある2群のt検定
  3. 対応のない2群のt検定

この3つのt検定、一度は目にしたことありませんか？

対応のあるt検定も対応のないt検定も、やっていることは本質的に同じ

t検定がまるで3種類あるかのように見えますが、これらは全て本質的に一緒です。

本質的に一緒であることを理解するために、まずはそれぞれの帰無仮説を整理してみましょう。

  1. 1群のt検定：A群の身⻑の母平均 = 定数
  2. 対応のある2群のt検定：A群の時点1の母平均 = A群の時点2の母平均
  3. 対応のない2群のt検定：A群の身⻑の母平均 = B群の身⻑の母平均

そして、上記の帰無仮説の右辺を左辺に移項させてみます。

  1. 1群のt検定：A群の身⻑の母平均 -定数 = 0
  2. 対応のある2群のt検定：A群の時点1の母平均 – A群の時点2の母平均 = 0
  3. 対応のない2群のt検定：A群の身⻑の母平均 – B群の身⻑の母平均 = 0

これを見ても明らかなように、「どれ」と「どれ」を比較しているかが異なるだけで、やっていることは同じなんです。

特に「対応のある2群のt検定」は混乱を起こしそうな言葉

その中でも、「対応のある2群のt検定」ってかなり誤解を招く表現だなと思います。

なぜなら、対応のある2群のt検定は、時点1のデータを「群1」、時点2のデータを「群2」として「2群」とカウントしているからです。

でも、対応のあるデータとは「同一サンプル（同一の群）」から得られている、時点だけが違うデータのことでした。

つまり、群って1つです。

あくまで違うのは「時点」だけ。

なので本質的には、時点1と時点2の変化量に対して1群のt検定をやっているのと一緒なんです。

＞＞もう統計で悩むのは終わりにしませんか？ 

↑1万人以上の医療従事者が購読中

その他の対応のあるデータに対する検定

対応のあるt検定の他にも、対応のあるデータに対する検定があります。

有名なのは以下の3つ。

  1. ウィルコクソンの符号付順位和検定
  2. 反復測定分散分析
  3. フリードマン検定

ウィルコクソンの符号付順位和検定については注意が必要です。

というのも、ウィルコクソンの順位和検定、というのもあるから。

「符号付」が付くと、対応のある検定。

「符号付」が無いと、対応のない検定。

違いは理解しておきましょう！

そして反復測定分散分析やフリードマン検定なんかもたまに見ますね。

それほど頻繁に見るような検定ではないので、「そんなのもあるんだ」ぐらいの認識でOKです！

対応のあるデータと対応のないデータをRで解析してみる

実際に、対応のあるデータと対応のないデータをRで解析してみましょう。

datariumというパッケージに含まれるサンプルデータを使います。

datariumパッケージは、統計解析と視覚化のためのデータセットを提供するRパッケージです。

このパッケージは、さまざまな統計手法を学習および実践するためのデータを体系的に整理して提供しています。サンプルデータを用いて、下記の解析を実施します。

  • 対応のあるデータで「対応のあるt検定」「Wilcoxonの符号付順位和検定」「スパゲティプロット」「Bland Altmanプロット」を実施する
  • 対応のないデータで「（Welchの）t検定」「Wilcoxonの順位和検定」を実施する

対応のあるデータで「対応のあるt検定」「Wilcoxonの符号付順位和検定」「スパゲティプロット」「Bland Altmanプロット」を実施する

まずは対応のあるデータの解析を実施します。mice2というデータを使います。

#1度だけ実施する。過去にインストールしたことがあれば実行しなくてOK
install.packages("PairedData")
install.packages("datarium")
install.packages("ggpubr")
install.packages("blandr")

# パッケージの読み込み
library(PairedData)
library(ggpubr)
library(blandr)

# データの読み込み
data("mice2", package = "datarium")

# データの確認
head(mice2, 3)

まずはデータを確認するために、BeforeとAfterの要約統計量を算出します。

# BeforeとAfterのそれぞれの要約統計量を計算
summary_stats_before <- mice2 %>%
  summarise(
    n = n(),
    mean = mean(before, na.rm = TRUE),
    sd = sd(before, na.rm = TRUE),
    median = median(before, na.rm = TRUE),
    min = min(before, na.rm = TRUE),
    max = max(before, na.rm = TRUE)
  )

summary_stats_after <- mice2 %>%
  summarise(
    n = n(),
    mean = mean(after, na.rm = TRUE),
    sd = sd(after, na.rm = TRUE),
    median = median(after, na.rm = TRUE),
    min = min(after, na.rm = TRUE),
    max = max(after, na.rm = TRUE)
  )

# 計算結果の表示
print(summary_stats_before)
print(summary_stats_after)

上記プログラムを実行すると、下記のような結果になります。

BeforeAfter
n1010
Mean200.56400.04
SD20.023..09
Median197.35405
Range(min-max)172.4-235377-445.8

次に、データを可視化してみます。

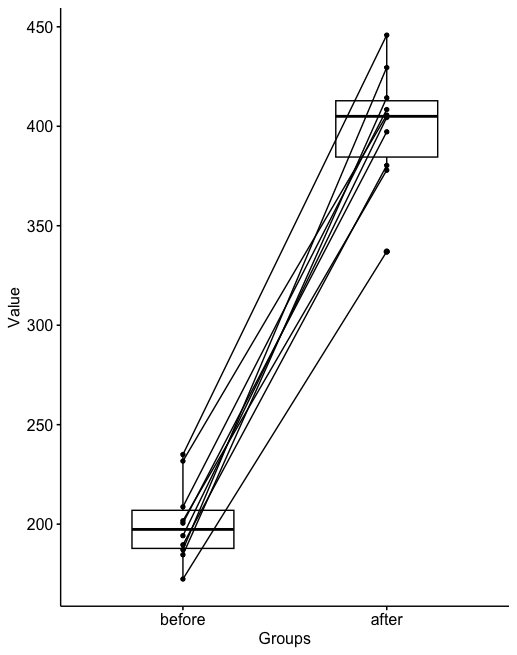
#BeforeとAfterでスパゲティプロットを作成しつつ、各時点の箱ひげ図を作成する
ggpaired(mice2, cond1 = "before", cond2 = "after",
         order = c("before", "after"),
         ylab = "Value", xlab = "Groups")

上記のプログラムを実行すると、下記のようにグラフが出力されます。

# 対応のあるt-testと結果の確認
result_t <- t.test(mice2$before, mice2$after, paired = TRUE)
print(result_t)

上記のプログラムを実行すると、下記のように結果が出力されます。

	Paired t-test

data:  mice2$before and mice2$after
t = -25.546, df = 9, p-value = 0.000000001039
alternative hypothesis: true mean difference is not equal to 0
95 percent confidence interval:
 -217.1442 -181.8158
sample estimates:
mean difference 
        -199.48

把握すべき数値は差と信頼区間とp値で、BeforeとAfterの差が-199.48でありその95%信頼区間は-217.14〜-181.82です。対応のあるt検定の結果、p<0.001であることがわかりました。 次に、Wilcoxonの符号付順位和検定を実施します。

# ウィルコクソンの符号付き順位和検定の実行
result_w <- wilcox.test(mice2$before, mice2$after, paired = TRUE)
print(result_w)

上記のプログラムを実行すると、下記のように結果が出力されます。

		Wilcoxon signed rank exact test

data:  mice2$before and mice2$after
V = 0, p-value = 0.001953
alternative hypothesis: true location shift is not equal to 0

ノンパラメトリック検定でもp=0.001953という結果が得られているため、結論としては対応のあるt検定と変わらない結果になりました。

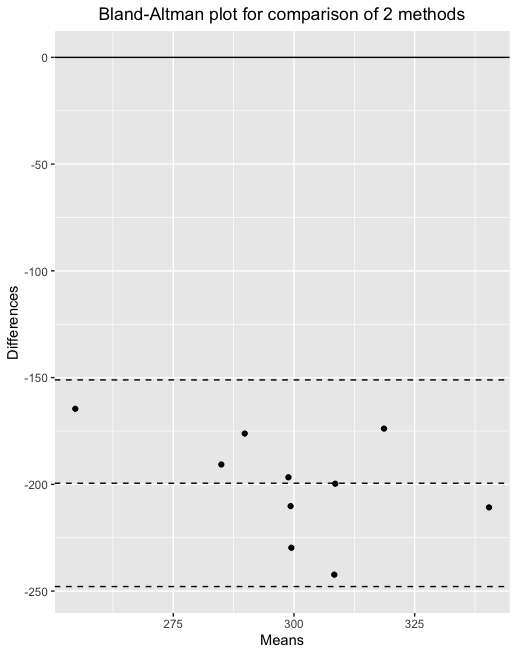
最後に、目的によっては対応のあるデータで実施することがある、Bland-Altman分析を実施します。

#Bland Altmanプロットを作成する
dat <- blandr.data.preparation(mice2$before,mice2$after,sig.level=0.95)

with(dat, blandr.display.and.draw(method1, method2, 
                      ciShading=FALSE, ciDisplay=FALSE))

すると、下記のようなグラフが作成されました。

対応のないデータで「（Welchの）t検定」「Wilcoxonの順位和検定」を実施する

では次に、対応のあるデータの解析を実施します。ここでは割愛しますが、要約統計量算出とグラフ化はいつでも重要ですので、対応のあるデータのプログラムを参考に要約統計量を算出してみてください。

# データの読み込み
data("iris")

# データの確認
head(iris)

# SetosaとVersicolorのデータ抽出
setosa <- subset(iris, Species == "setosa")
versicolor <- subset(iris, Species == "versicolor")

# 対応のないt検定と結果の表示
t_test_result_unpaired <- t.test(setosa$Sepal.Length, versicolor$Sepal.Length)
print(t_test_result_unpaired)

すると、下記のような結果が出力されました。

	Welch Two Sample t-test

data:  setosa$Sepal.Length and versicolor$Sepal.Length
t = -10.521, df = 86.538, p-value < 2.2e-16
alternative hypothesis: true difference in means is not equal to 0
95 percent confidence interval:
 -1.1057074 -0.7542926
sample estimates:
mean of x mean of y 
    5.006     5.936

各群（Setosa群とVersicolor群）の平均、そして平均値の差の95%信頼区間（-1.11〜-0.75）が出力され、p<0.001であることがわかります。e-16は「10のマイナス16乗」の意味で、p値がかなり小さいことを示しています。

次に、Wilcoxonの順位和検定を実施します。

# ウィルコクソンの順位和検定の実行と結果の表示
result <- wilcox.test(setosa$Sepal.Length, versicolor$Sepal.Length)
print(result)

上記のプログラムを実行すると、下記のように結果が出力されます。

	Wilcoxon rank sum test with continuity correction

data:  setosa$Sepal.Length and versicolor$Sepal.Length
W = 168.5, p-value = 8.346e-14
alternative hypothesis: true location shift is not equal to 0alternative hypothesis: true location shift is not equal to 0

ノンパラメトリック検定でもp<0.001という結果が得られているため、結論としてはt検定と変わらない結果になりました。

まとめ

いかがでしたか？

この記事では「対応のあるデータ・対応のないデータとは？例を用いてわかりやすく解説！」ということでお伝えしました。

  • 対応のあるデータとは？対応のないデータとは？違いって何？
  • 対応のあるt検定と対応のないt検定をわかりやすく解説
  • その他の対応のある検定

これらのことがわかるようになったのなら幸いです！

こちらの内容は動画でも解説していますので、併せてご確認くださいませ。

個々の統計検定の説明
よかったらシェアしてね！
  • URLをコピーしました！
  • URLをコピーしました！

リサーチクエスチョン探し？データ分析？論文投稿？、、、で、もう悩まない！

第1章：臨床研究ではなぜ統計が必要なのか？計画することの重要性
  • 推定ってどんなことをしているの？
  • 臨床研究を計画するってどういうこと？
  • どうにかして標本平均を母平均に近づけられないか？
第2章：研究目的をどれだけ明確にできるのかが重要
  • データさえあれば解析でどうにかなる、という考え方は間違い
  • 何を明らかにしたいのか？ という研究目的が重要
  • 研究目的は4種類に分けられる
  • 統計専門家に相談する上でも研究目的とPICOを明確化しておく
第3章：p値で結果が左右される時代は終わりました
  • アメリカ統計協会（ASA）のp値に関する声明で指摘されていること
  • そうは言っても、本当に有意差がなくてもいいの…？
  • なぜ統計専門家はp値を重要視していないのか
  • 有意差がない時に「有意な傾向があった」といってもいい？
  • 統計を放置してしまうと非常にまずい
第4章：多くの人が統計を苦手にする理由
  • 残念ながら、セミナー受講だけで統計は使えません。
  • インプットだけで統計が使えない理由
  • どうやったら統計の判断力が鍛えられるか？
  • 統計は手段なので正解がないため、最適解を判断する力が必要
第5章：統計を使えるようになるために今日から何をすれば良いか？
  • 論文を読んで統計が使えるようになるための5ステップ
第6章：統計を学ぶために重要な環境
  • 統計の3つの力をバランスよく構築する環境

『統計を身につける5つのステップ』を
通常1,650円 → 無料でプレゼント

以下のボタンをクリックして、画面に出てくる指示に従って、必要事項を記入してください。

通常価格：1,650円　→　無料でお届け

【無料】統計を使いこなすための秘策を学ぶ

関連記事

コメント

コメント一覧 （3件）

コメントする

目次