あなたは、P値って何なのか、考えたことはあるでしょうか？
以前、参加したことのある統計セミナーで「P値を説明してください」という問題が出たことがあります。
あなたはどう回答しますか？
そのセミナーの中で、面白かった回答がありました。
「0.05を切ったら嬉しいもの」
まぁ確かにな、と思いました。
P値ほど、誤解されて使われているものはありません。
とりあえず0.05を下回ったら、何も考えずにOK。
そんな使い方をされていることが多い。
でも、実はそれ以上にP値は深い意味を持っています。
このページでぜひともP値は何かを学んでいきましょう！
手計算での求め方を、コイン投げを例にして解説しますね！
Contents
P値とはどんな意味かをわかりやすく教えて！
まずは、P値って何かを考えたことはありますか？
P値。ピーチ。
・・・桃？？
冗談はさておき、P値は「何かの確率」を示しています。
ちなみにP値の「P」は「Probability」の略です。「確率」ですね。
重要なのは、「何の」確率か、ということです。
P値（p-value）の意味は帰無仮説下で、その結果以上（以下）が出る確率である
正解を先に言います。
P値は以下の言葉で言い換えることができます。
帰無仮説を考えている時に、得られた結果より極端な結果が出る確率
わかりますか？
おそらく文字だけで説明されても全然わからないと思いますので、コインを例に考えてみましょう。
P値の求め方を手計算で求めながら、意味をコイン投げの事例で学ぶ
コイントスで、表が出たら1万円をもらえる、裏が出たら1万円を支払う、という場面を想定します。
そしてあなたは、そのコインがイカサマであれば参加しない。
つまり裏が出やすいコインである、ということであれば参加したくないと思っています。
では、その「イカサマなコインである」を統計学的に証明していきましょう。
まずは、帰無仮説と対立仮説を考えます。
今回のコイン投げの場合、帰無仮説と対立仮説はどのようになるでしょうか？
このようになりますね。
帰無仮説は「コインはイカサマでない」
対立仮説は「コインはイカサマである」
ではここで一つ問題です。
帰無仮説「コインはイカサマでない」という前提に立った場合に、裏（若しくは表）が出る確率はどうなるでしょうか？
帰無仮説を考えている場合とは言い換えると、「コインはイカサマではない」という場合を想定しています。
つまり、あなたが普段持っている100円玉を投げた時に、どんな確率で裏（もしくは表）が出るかということです。
当然わかりますよね。
帰無仮説「コインはイカサマでない」という前提に立った場合に、裏（若しくは表）が出る確率は1/2である
P値を手計算するために10人のコイン投げの結果を観察してみる
そして、このコインがイカサマかどうかを確かめるために、自分より前の10人の結果を調べることにしました。
10人の結果を見てみましょう。
帰無仮説では表が出る確率は1/2であるため、10回中５回は表が出るはずです。
ですが、たまたま表が７回でたり、反対に２回しか出ない時もあります。
つまり、10人のコイン投げで表が出る回数は、0〜10回があり得ます。
あなたの想像の通り、10回コインを投げたうち、10回表が出ることは稀で、0回表が出ることも稀です。
そんなあなたの考えを確率で表現したのが以下の表です。
| 表が出る回数 | 0 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 |
| 確率 | 0.001 | 0.010 | 0.044 | 0.117 | 0.205 | 0.246 | 0.205 | 0.117 | 0.044 | 0.010 | 0.001 |
| 累積確率 | 0.001 | 0.011 | 0.055 | 00.172 | 0.377 | 0.623 | 0.828 | 0.945 | 0.989 | 0.999 | 1.000 |
これは、二項確率というものを計算しています。
例えば「表が出る回数3」の確率というのは、10回コイン投げをした場合に、3回表が出る確率を二項確率の計算式を元に計算しています。
表を見ると、あなたが想像している通り、10回中５回表が出る確率が24.6%と一番高いです。
一方で、０回や10回表が出る確率は0.1%と、一番小さい確率です。
一番下の行は、累積確率と呼ばれ、左から順に確率を足し合わせたものになります。
例えば「表が出る回数が2回」のところにある累積確率（0.055）は、0回の確率と1回の確率と2回の確率を全て足し合わせた結果になっています。
つまり、0.001+0.010+0.044=0.055です。
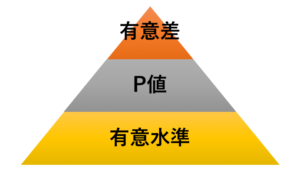
P値とは累積確率
そして、この「累積確率」がP値になります。
・・・たぶん、ぽかーんとしている方が大半かもしれません。。
ですが、そうなのです。
一般化してP値を言葉で置き換えます。
P値とは、帰無仮説下（表が出る確率は1/2である）での、その結果より極端な結果が出る確率
このP値が0.05より小さければ、想定している仮説（帰無仮説）の下では、その結果が出る確率は0.05以下でしかない。
このコイン投げの例でいうと、「1/2は表が出ると想定しているのに、その結果が出る確率は0.05以下しかない」
そのような結果が出た場合に、想定している仮説が間違っている（＝帰無仮説が間違っている）んじゃないか。
と考えます。
つまり、帰無仮説を棄却し、対立仮説を採択するのです。
このコインの例では、表が1回以下である確率が0.011であり、2回以下である確率が0.055です。
そのため、イカサマであると判断する数値的な閾値を0.05とした場合には、10回分の結果から、表が1回以下であればこのコインはイカサマであると結論付け、ゲームには参加しないという判断を下すという流れです。
数値としてのp値は「要約統計量の一つ」である
統計学としての理論的なp値は、上記で解説した「確率」として定義されるものです。
しかしそれはあくまで、数学的概念としてのp値。
一方で、出力された「数字としてのp値」は、検定統計量を変換して計算された、要約指標の一種です。
確率変数と言っても良い指標であり、確率変数であれば何らかの確率分布に従う。（引用：医学のための因果推論I, p51）
特に気をつけていただきたいのは、サンプルサイズが小さい時には、p値の確率的変動は不安定で、到底信頼できるものではないということ。
仮説検定の目標は、αエラーとβエラーを制御することであって、適切なサンプルサイズ設計がなされていることが前提。
医学研究では、p値はデータの要約指標という観点で扱うのがよく、その意味では推定値や信頼区間など大差ないのだから、特別扱いすべきではありません。
むしろ、信頼区間の方が情報量が多く、データを理解するために役立つ指標です。
P値に関するまとめ
P値は帰無仮説下で、その結果以上（以下）が出る確率である。
つまり、帰無仮説下での確率が有意水準の0.05を下回った場合、帰無仮説を考えていることが間違っているのではないかと判断して棄却し、対立仮説を採択する。
P値に関して動画で解説しています。
ぜひブログ記事を併せて確認してみてください。
第1章：臨床研究ではなぜ統計が必要なのか？計画することの重要性
第2章：研究目的をどれだけ明確にできるのかが重要
第3章：p値で結果が左右される時代は終わりました
第4章：多くの人が統計を苦手にする理由
第5章：統計を使えるようになるために今日から何をすれば良いか？
第6章：統計を学ぶために重要な環境
もしあなたがこれまでに、何とか統計をマスターしようと散々苦労し、何冊もの統計の本を読み、セミナーに参加してみたのに、それでも統計が苦手なら…
私からプレゼントする内容は、あなたがずっと待ちわびていたものです。
