T検定とは？具体例でわかりやすく！F検定で等分散の確認が必要？

統計の世界では最も有名な検定であると言っても過言ではない、T検定。

このページでは、T検定について具体例を用いてわかりやすく解説します。

検定は、帰無仮説と対立仮説を確認することがすごく重要なので、帰無仮説と対立仮説をどう確認するか、というポイントも解説。

そのほかにも、この記事を見ればこれらのことがスッキリしますよ！

• T検定の前にはF検定をする？
• 等分散の過程が必要？
• １標本と２標本？
• 自由度ってどう求めるの？

T検定とは何？具体例でわかりやすく解説！

「世の中にはいろんな検定があるけど、それぞれがどんな検定なのかが分かりません・・・。」

私のところに、そのような質問が多々寄せられます。

確かに統計の検定は数が多くて、結局何をやっているのかが分かりにくかったりします。

そんな時のアドバイス。

どんな検定をしているかを手っ取り早く、そして正確に把握するにはあるものを見ればいいんです。

それは、「帰無仮説と対立仮説」です。

帰無仮説と対立仮説って難しそうな用語ですが、それほど難しいものではありません。

帰無仮説と対立仮説は、「何を検定しているのかを直接文章として記載しているもの」です。

そのため、その検定が何をやっているか、帰無仮説と対立仮説を確認することで一目瞭然なのです。

ということで、本サイトの検定に関する記事では、必ず帰無仮説と対立仮説を載せるようにしますね。

T検定の帰無仮説と対立仮説

では早速、T検定の帰無仮説と対立仮説は何かを見てみましょう。（2標本のT検定の場合）

この帰無仮説と対立仮説を確認して、何がわかりますか？

T検定は平均値に対する検定であることが分かりますよね。

T検定は有名なので、仮説を見なくても「平均値に対する検定だ」とわかるかもしれません。

ですが、これから勉強をするにつれ、初めてその名前を聞く検定が、今後出てくると思います。

その時には、帰無仮説と対立仮説を確認するようにしましょう。

超有名な分散分析でさえ、その帰無仮説と対立仮説をちゃんと確認しないことには、結果を正しく解釈することができません。

T検定を実施する具体例

T検定は平均値を検定する統計的手法だということがわかりました。

であれば、具体的にどんな時にT検定を実施できるでしょうか？

平均値を使うということは、データが「連続量（量的データ）であること」と「正規分布にしたがっていること」の2点が重要です。

そのため、以下のような場合にはT検定が使えますね。

• 新薬群とプラセボ群の患者さんの身長の違いを知りたい
• A大学とB大学の学生の体重の違いを知りたい

T検定にはたくさん種類がある？1標本や2標本、対応ありや対応なしとは？

T検定と検索すると、1標本のT検定とか2標本のT検定とか、2種類出てきますよね。

それらの違いって何？って疑問に思ったことないでしょうか。

私も統計を勉強し始めた頃、全然イメージができませんでした。

でも実は、それほど難しい概念ではないです。

一言でいうと、データが1種類か2種類かの違いです。

例えば。

1. ある時点の、A群だけの身長データ。
   • これは１標本。
2. ある時点の、A群とB群の身長データ
   • これは２標本。
3. ある時点（時点１）の、A群だけのデータと、その１年後（時点２）の、A群だけの身長データ
   • これも２標本。ですが、対応のある２標本と言われています。

で、この1標本と2標本で、T検定のやり方は何か違いがあるの？と思いますよね。

実は、ほぼ一緒です！

なぜかを考えるのに、それぞれの帰無仮説を確認してみましょう。

1. A群の身長の母平均＝０（定数）
2. A群の身長の母平均＝B群の身長の母平均
3. A群の時点１の母平均＝A群の時点２の母平均

で、2と3については、右辺を左辺に持っていく。

すると、結局こうなります。

1. A群の身長の母平均＝０（定数）
2. A群の身長の母平均- B群の身長の母平均＝０
3. A群の時点1の母平均- A群の時点2の母平均＝0

引き算があるかどうかの違いだけで、３つともほぼ一緒じゃないですか？

なので、1標本とか2標本とかによって何かしら新しく考えることがあるわけではなく、結局は同じことを検定しています。

＞＞対応のあるデータ・対応のないデータとは？

T検定をするには事前にF検定を実施して等分散性の確認が必要？

T検定を調べていくと、もう一つ条件が出てきます

それは、等分散性。

等分散性とは文字通り、A群とB群のデータの分散が同じである性質、ということ。

これがあるために一昔前は、以下のフローでT検定を実施されることが多くありました。

Twitterでも悩んでいる方がいましたね。

(研究の話)　結局F検定やって等分散か調べた後にt検定の種類選ぶのがよいのか最初からウェルチやった方がよいのか

— サカユリヤはミジンコストラップ作る人 (@sakayuriya) December 30, 2018

つまり、このような方法をやる必要があるか？

ということです。

F検定（等分散性の検定）を実施
↓
もし有意になれば、等分散ではないとして、WelchのT検定（等分散性の条件がいらないT検定）を実施する。
↓
もし有意でなければ、等分散として、StudentのT検定（等分散性の条件が必要なT検定）を実施する。

私も大学院時代にマイクロアレイ解析をしていた時は、この方法を使っていました。

ですが、今ではこのような方法はほとんど見られません。

理由は大きく2つ。

ということで、WelchのT検定さえ使っておけば、誰も文句言わないです。

等分散を仮定するスチューデントのT検定の方がなぜか有名なので、スチューデントのT検定を実施することが多いかもしれませんが、スチューデントのT検定は「正規性」＋「等分散」の2つの仮定が必要。

それよりも、「正規性」の一つの仮定さえあれば使えるWelchの方がオールマイティーです。

また、分散が実際に等しい場合には検出力がいくらか失われますが、そうでない場合には検出力が増加するという研究結果がありますので、Welchのt検定を実施することをお勧めします。

T検定における自由度の考え方とは？

T検定を実施するのに必要なもう一つの知識。

それが自由度です。

自由度に対する考え方については、別ページで解説しているのでそちらを参照してください。

なのでここでは、T検定に特化した自由度の考え方だけお伝えします。

結論から言うと、T検定の自由度は「データの数ー群の数」です。

例えば、２群のデータで、各群１０個のデータ。

計２０個のデータがあったとします。

この時の自由度は、２０−２＝１８となります。

RでT検定を実践する！

では実際に、サンプルデータを用いて等分散かどうかの判断と、統計学的検定を実施します。

Rをダウンロードした際に含まれている「iris」というデータを使います。

具体的には、以下の3つを実施します。

1. 2種類のアヤメ（setosa, versicolor）ごとにがくの長さ（Sepal.Length）のヒストグラムを作成
2. 2種類のアヤメ（setosa, versicolor）ごとにがくの長さ（Sepal.Length）の要約統計量を算出
3. 上記2つの結果をもとにしてがくの長さ（Sepal.Length）の統計学的検定を実施する

2種類のアヤメ（setosa, versicolor）ごとにがくの長さ（Sepal.Length）のヒストグラムを作成

まずはヒストグラムを作成します。Rでは下記のようにプログラムを実行することによってヒストグラムを作成できます。

#1度だけ実施する。過去にインストールしたことがあれば実行しなくてOK
install.packages("ggplot2") 

#ggplot2を呼び出す
library(ggplot2)

# データの読み込み
data("iris")

# SetosaとVersicolorのデータ抽出
setosa <- subset(iris, Species == "setosa")
versicolor <- subset(iris, Species == "versicolor")

# SetosaとVersicolorのデータを一つにまとめる
iris_new <- rbind(setosa,versicolor)

# データの確認
head(iris_new)

# ヒストグラムを作成
ggplot(iris_new, aes(x = Sepal.Length, fill = Species)) + 
  geom_histogram(position = "identity", alpha = 0.8) + 
  theme_minimal() + 
  labs(title = "Histgram of Sepal.Length", x = "Sepal.Length", y = "Frequency")

上記のプログラムを実行すると、下記のようにヒストグラムが作成されます。

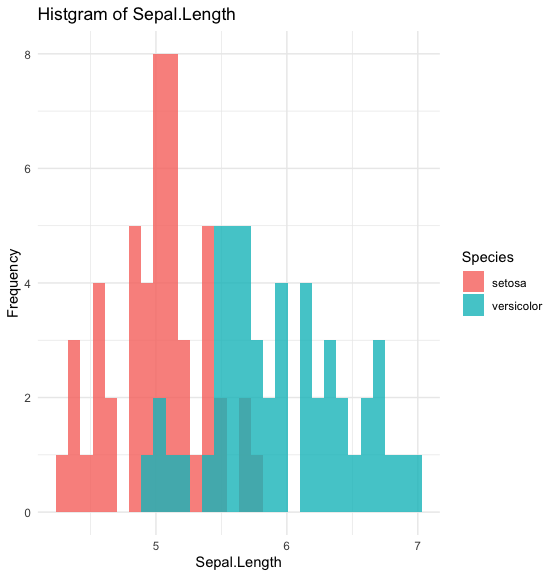
setosaよりもversicolorの方がばらつきは大きいように見えます。

また、どちらの種類も、真ん中が一番盛り上がっており、左右に少なくなっているため、正規分布とみなしてもいいのではないかと思われます。

2種類のアヤメ（setosa, versicolor）ごとにがくの長さ（Sepal.Length）の要約統計量を算出

要約統計量を算出します。Rでは下記のようにプログラムを実行することによって要約統計量を算出できます。

#1度だけ実施する。過去にインストールしたことがあれば実行しなくてOK
install.packages("dplyr")

# dplyr パッケージを読み込む
library(dplyr)

# データの読み込み
data("iris")

# データの確認
head(iris)

# SetosaとVersicolorのデータ抽出
setosa <- subset(iris, Species == "setosa")
versicolor <- subset(iris, Species == "versicolor")


# 種類ごとにがくの長さ（Sepal.Length）の要約統計量を計算
summary_stats_setosa <- setosa %>%
  summarise(
    n = n(),
    mean = mean(Sepal.Length, na.rm = TRUE),
    sd = sd(Sepal.Length, na.rm = TRUE),
    var = sd^2,
    median = median(Sepal.Length, na.rm = TRUE),
    min = min(Sepal.Length, na.rm = TRUE),
    max = max(Sepal.Length, na.rm = TRUE)
  )

summary_stats_versicolor <- versicolor %>%
  summarise(
    n = n(),
    mean = mean(Sepal.Length, na.rm = TRUE),
    sd = sd(Sepal.Length, na.rm = TRUE),
    var = sd^2,
    median = median(Sepal.Length, na.rm = TRUE),
    min = min(Sepal.Length, na.rm = TRUE),
    max = max(Sepal.Length, na.rm = TRUE)
  )


# 計算結果の表示
print(summary_stats_setosa)
print(summary_stats_versicolor)

上記のプログラムを実行すると、下記のような結果になりました。

	Setosa	Versicolor
n	50	50
Mean	5.01	5.94
SD	0.352	0.516
Var	0.124	0.266
Median	5	5.9
Range(min-max)	4.3-5.8	4.9-7

分散（Var）をみると、Setosaは0.124でありVesicolorは0.266でした。

また、平均値と中央値がほぼ同じ値であることがわかります。

ヒストグラムと要約統計量を確認すると、分散が同じではなさそう、正規分布とみなしても良さそう、と結論づけることができます。

上記2つの結果をもとにしてがくの長さ（Sepal.Length）の統計学的検定を実施する

ヒストグラムと要約統計量を確認すると、分散が同じではなさそう、正規分布とみなしても良さそう、と結論づけたため、Welchのt検定を実施します。

# welchのt検定と結果の表示
t_test_result_unpaired <- t.test(setosa$Sepal.Length, versicolor$Sepal.Length)
print(t_test_result_unpaired)

すると、下記のような結果が出力されました。

	Welch Two Sample t-test

data:  setosa$Sepal.Length and versicolor$Sepal.Length
t = -10.521, df = 86.538, p-value < 2.2e-16
alternative hypothesis: true difference in means is not equal to 0
95 percent confidence interval:
 -1.1057074 -0.7542926
sample estimates:
mean of x mean of y 
    5.006     5.936

各群（Setosa群とVersicolor群）の平均、そして平均値の差の95%信頼区間（-1.11〜-0.75）が出力され、p<0.001であることがわかります。e-16は「10のマイナス16乗」の意味で、p値がかなり小さいことを示しています。

T検定に関するまとめ

• その検定が何をやっているかは、帰無仮説と対立仮説を見ればわかる。
• T検定は、平均値の違いを検定する方法。
• 1標本とか2標本とかあるけど、本質は一緒。
• WelchのT検定さえ使っておけば、間違いはない。

また、動画でもT検定に関して解説していますので、合わせてご確認いただけると理解が進むはずです。