分散分析とは？わかりやすく分散分析表の見方やf値とp値の意味を解説！

この記事では「分散分析とは？わかりやすく分散分析表の見方やf値とp値の意味を解説！」ということで解説します。

 

データを解析したことのあるあなたなら、一度は目にしているであろう分散分析（ANOVA）。

「分散」分析というだけあって、分散を検定している？？

そんなイメージを持っているのはあなただけではないでしょう。

何を隠そう、私も最初はそうでした。

あれ、分散を検定しているなら、F検定と何が違うの？って感じでした。

 

今日はそんな分散分析の解説を簡単にわかりやすく。

分散分析表の見方やf値やp値の意味も解説しています。

 

また、分散分析を理解することは、共分散分析の基礎を理解することにもなります。

ぜひしっかり理解しておいてくださいね！

 

分散分析（ANOVA）とは？T検定との違いは何？

まずは、分散分析が何を検定しているのか、結論を述べましょう。

 

分散分析ほど、その検定の名前と、何を検定しているかのギャップが大きいものはないです。

だって分散と言いながら、母平均を検定していますからね。

つまり、T検定と一緒。

ではなぜ分散分析と呼ぶかというと、分散を使って母平均を検定しているからです。

ややこしいですよね。

ややこしいですが、でも一度覚えてしまえば忘れないと思いますので、ぜひこの機会に覚えてください。

 

分散分析はT検定と何が違うの？

分散分析がT検定と同じであれば、T検定と何が違うのか？ということが疑問になりますよね。

違いは、扱う群の数。

T検定は1群と2群の時でしたが、分散分析は3群以上の時に使う検定です。

 

 

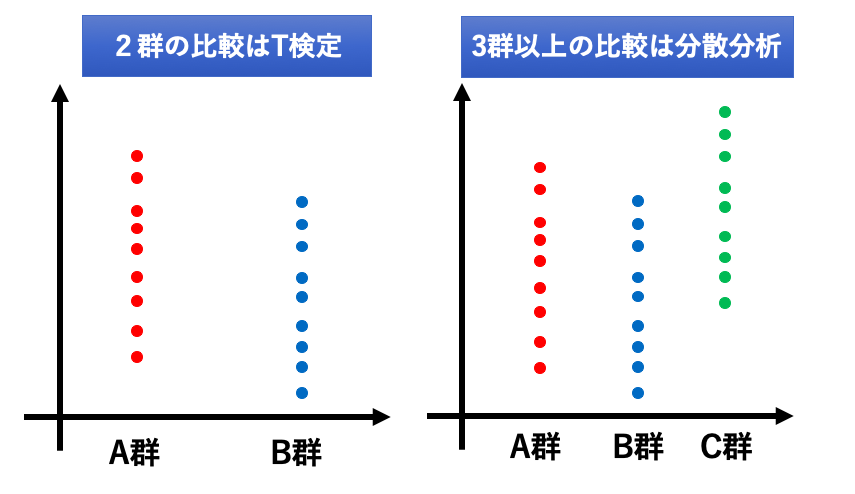
では、３群の平均値をどのように比較しているのか。

それを知りたいのであれば、T検定でも解説したように「帰無仮説と対立仮説」を確認するのでしたね。

 

分散分析の帰無仮説と対立仮説

では早速、分散分析の帰無仮説と対立仮説を見てみましょう。

簡単のために、3群の分散分析の場合を記載します。

 

 

注目したいのは分散分析の対立仮説

帰無仮説と対立仮説が確認できました。

分散分析ほど、ちゃんと帰無仮説と対立仮説を確認したほうがいい検定はないですね。

 

というのも、注目してほしいのが、対立仮説。

もう一度対立仮説を記載しておきます。

 

 

この対立仮説は何を言っているのか。具体的に想像できますか？

実は、こんなことを言っています。

 

• A群の母平均≠B群の母平均＝C群の母平均、という結果が出たとしても有意になります。
• A群の母平均＝B群の母平均≠C群の母平均、という結果が出たとしても有意になります。

 

逆にいうと、こういうことです。

 

 

これ、めちゃめちゃ重要です！

ぜひとも、しっかりと把握してください。

 

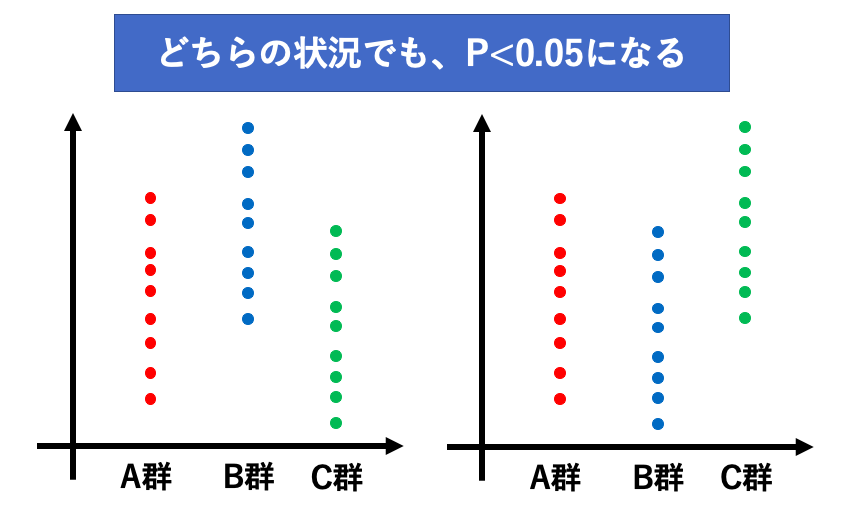
例えば以下の図で、どちらの状況もP<0.05であるとします。

同じ「P<0.05」だったとしても、左の図のようにA群とB群で差があるのかもしれないし、右の図のようにA群とC群で差があるのかもしれない。

分散分析のP値をみても、どの群間で差があるのかが分からないのです。

 

分散分析表の見方は？f値やp値の意味

分散分析では必ず出てくる、分散分析表。

分散分析表に関しては覚えておいていいですね。

丸暗記してもいいレベルです。

分散分析表は以下のような表です。

 

要因	平方和S	自由度df	平均平方V	F値
群	S(群)	df(群) (群の数-1)	V(群) （=S(群)/df(群))	V(群)/V(残)
残差	S(残)	df(残) (df(全)-df(群))	V(残) （=S(残)/df(残))
全体	S(全)	df(全) （全データ数-1）

 

平方和、自由度、平均平方があって、F値が出てきます。

そしてF値は、群の不偏分散と残差の平均平方の比です。

（平均平方は不偏分散とも言われます。）

F値があれば、F分布表を見てP値を出せますよね。

つまり、（不偏）分散を使ってF値を算出　→　P値を出力

だから、分散分析と言われるのです。

（繰り返しですが、平均平方は不偏分散とも言われます。）

 

そして、F値が大きいとP値が小さくなります。

じゃあF値が大きくなる時は？

それは、群の要因における分散（バラツキ）のほうが、残差の要因における分散よりも大きいときです。

つまり、偶然による誤差（残差の分散）よりも、群による誤差（群の分散）のほうが大きいから、どこかの群間に違いが出ている、と結論付けるのです。

 

自由度に関しては大丈夫ですか？

カイ二乗検定のところで自由度を解説しておりますので、ぜひ確認しておいてくださいね。

 

一元配置分散分析や二元配置分散分析って何？

分散分析を調べていると、必ず出てくる「一元配置分散分析」や「二元配置分散分析」という言葉。

私も統計を学び始めた時につまずいた用語なので、ここで整理しておきます。

 

一元配置分散分析とは？

一元配置分散分析とは、１つの因子による平均値の差を分析する方法です。

「一元配置」という用語が難しく思いますが、要は１種類の因子（データ）の影響による、水準間の平均値の差を解析する場合に用いる手法です。

例えば、上記の例にある「A群、B群、C群」の３水準のデータを持った「群」という１つの因子で平均値の差がどうであるかを解析するとき。

そんな時は、一元配置分散分析を使う、ということになります。

 

二元配置分散分析とは？

一方、二元配置分散分析とは、２つの因子による平均値の差を分析する方法です。

例えば、「A群、B群、C群」の３水準のデータを持った「群」という因子と、「男性、女性」という２水準のデータを持った「性別」という因子の、２つの因子の組み合わせでの平均値の差を分析したい場合。

そんな時は、二元配置分散分析を使う、ということになります。

 

この「群」と「性別」で二元配置分散分析をする場合には、目的は３つあります。

1. 「群」の３水準間で平均値に違いがあるかを知りたい
2. 「性別」の２水準間で平均値に違いがあるかを知りたい
3. 群と性別の組み合わせの６水準間（３水準×２水準）で平均値に違いがあるかを知りたい

 

基本的には、3つ目の目標である2つの因子の組み合わせに興味があることが多いです。

ですが、どこに興味があるかは、研究目的によりますので個別に吟味することが重要です。

 

分散分析の後に、多重比較（事後検定）をする意味

前述の通り、分散分析の対立仮説を読み解くと、「分散分析で有意になったとしても、どの群の間の平均が異なるか、ということまでは分からない」ということになります。

では、どの群の間での平均値が異なるかを調べよう、と思いますよね。

つまり、分散分析をした後に2群検定の多重比較（事後検定）をする、ということですね。

 

すると、以下のような手順で検定をするということになります。

分散分析ではどの群の間で有意になったのか分からない。

だったら分散分析の後に、どの群間で違いがあるかを見ようじゃないか。

そんな発想です。

自然な気がしますね。

 

ですが私は、その手順を全然推奨しません。

理由は明確。

分散分析と2群検定では、知りたいことが違うからです。

 

さらに、検定を２回以上実施すると、多重性の問題という新たな問題が発生してしまいます。

 

分散分析と2群比較を使う場面を考えてみる

では、分散分析と2群検定の多重比較の使い分けはどのようにすれば良いのでしょうか。

私が使い分けるとしたら、このように使い分けます。

 

• 分散分析：全群で差がないことを積極的に知りたいとき。
• 2群検定の多重比較：どこかで差があることを積極的に知りたいとき。

 

具体的にどういう場合か、例を出して考えてみましょう。

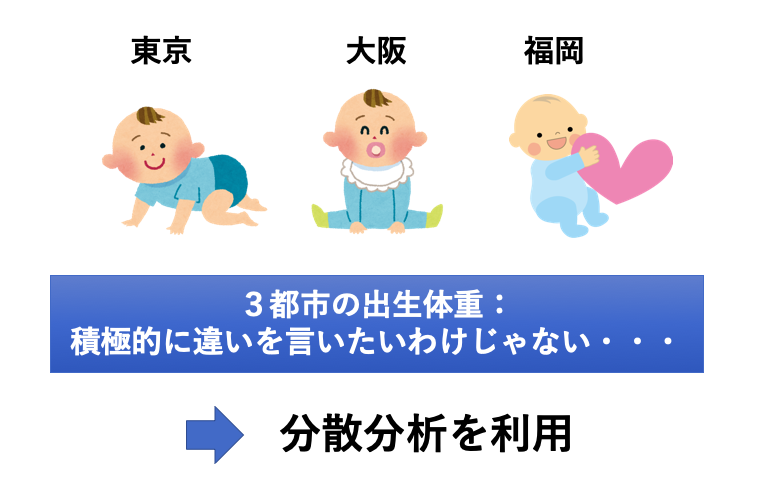
例えば、東京、大阪、福岡の3都市の出生時の体重の違いを比較する。

これ、別に積極的に差があることを言いたいわけじゃないですよね。

そんな時は、念のため分散分析をする。

でもここで重要なのは、「検定結果が有意じゃなかったとしても、”同じ”という結論は得られない」ということに注意すること。

分散分析をしました　→ 有意じゃなかった　→ 3都市の出生時の体重は同じ

というのは、NGということです。

論文や学会発表でも、3群以上あるときの被験者背景情報の集計で分散分析のp値を見ることがあります。

これもまた「群間で背景情報に差がない」ことを伝えたい意図なのかなと思います。

あくまで有意じゃない時の結論は「差があるとは言えない」ということだけで、積極的に「同じ」であることを言えないので注意してください。

 

では、プラセボ、新薬、標準治療の3つの治療での違いを比較する。

この時、分散分析をしたってしょうがないですよね。

だって、プラセボvs新薬、プラセボvs標準治療の2つは、積極的に差が言いたいから。

分散分析をして有意でした！ってなったとき。

プラセボ、新薬、標準治療の3つの治療の「どこかに差がある」ということです。

「で？」って感じですよね。

それなら最初から、プラセボvs新薬、プラセボvs標準治療、新薬vs標準治療、の2群比較を、多重性を考慮しながら3つ実施したほうが素直です。

 

2群で分散分析するとt検定と同じ結果になる

ちょっとした知識です。

読み飛ばしても、あなたのこれからの統計ライフに影響はないでしょう。

でも、知ると「えー！！」ってなります。

 

分散分析は3群以上での母平均の比較でしたね。

じゃあ、2群で分散分析やってみたらどうなるか？

あなたはどうなると思いますか？

実は、T検定と同じことをやっています！

これは面白いですよね。

証明はややこしいので、スキップします。笑

 

分散分析（ANOVA）をEZRで実践したり動画で学ぶ

分散分析（ANOVA）をEZRで実践する方法を、別記事で解説しています。

EZRとは無料の統計ソフトであるRを、SPSSやJMPなどのようにマウス操作だけで解析を行うことができるソフトです。

EZRもRと同様に完全に無料であるため、統計解析を実施する誰もが実践できるソフトになっています。

2019年5月の時点で英文論文での引用回数が2400回を超えているとのことで、論文投稿するための解析ソフトとしても申し分ありません。

これを機に、EZRで統計解析を実施してみてはいかがでしょうか？

 

＞＞EZRで分散分析（ANOVA）を実践する。

 

また、分散分析に関して動画で解説しています。

この記事を見ながら視聴すると、分散分析に関してかなり理解が進みますので、ぜひ試聴してみてください。

 

分散分析に関するまとめ

• 分散分析は、3群以上の母平均の検定である。
• 帰無仮説と対立仮説を確認すると、分散分析で有意になったとしても、どの群の間の平均が異なるか、ということまでは分からない、ということが言える。
• 分散分析をした後に2群検定の多重比較は推奨しない。