統計を学ぶと必ず出てくる「検定統計量」という用語。
なんとなく分かるようで分からないなぁ。。といった方も多いのではないでしょうか。
私も統計を学び始めた頃には「検定統計量ってなんのためにあるの??」ということを疑問に思ったものです。
この記事では、統計学的仮説検定で基本的な概念である検定統計量と、検定統計量を利用する理由について説明していきます。
また、検定統計量とP値や棄却域との関係についても説明します。
検定統計量とは?どんな検定統計量があるのか?

検定統計量を一言で言えば、「検定するための値」ということ。
統計学は確率を扱います。コイン投げやサイコロの例だと、「表が出る確率」とか「1の目が出る確率」など、直接確率を扱うことができます。
一方で、身長や体重、HbA1cなど、臨床研究で扱うようなデータに対して「確率」といっても、なかなかピンとこないですよね。。。
そのため、通常のデータに対して統計学的検定ができるよう、確率として扱うことができるように変換した値のことを検定統計量と言います。
統計学的検定といえば、T検定やカイ二乗検定などが有名ですよね。
このブログでもこれまでに、T検定やカイ二乗検定などいくつかの検定法について説明しました。
>>>>T検定とは具体例でわかりやすく!F検定で等分散の確認が必要?
>>>>F検定とは?わかりやすくF分布のグラフからP値の読み取り方まで
>>>>カイ二乗検定とは?分かりやすく例で分割表の検定の計算式も簡単に!
これらの検定を行う方法の基本概念は、
- あらかじめ帰無仮説を立てておき、
- それぞれの手法に基づきt値やF値、カイ二乗値を計算し、
- その値が有意水準と比べて値が小さいならば、
- 帰無仮説を棄却し、対立仮説を採用する
というものでした。
帰無仮説と対立仮説については以下のページでも扱っています。
>>>>帰無仮説とは?対立仮説との違いを例題で簡単に。検定で棄却できないときは?
そして、統計学的検定で出てきた、t値やF値、カイ二乗値のような値のことを「検定統計量」と呼びます。
代表的な検定統計量を一覧にまとめてみました。
| 検定名 | 検定統計量 | 目的 |
| T検定 | t値 | 母平均に差があるかどうか |
| F検定 | f値 | 母分散に差があるかどうか |
| カイ二乗検定 | カイ二乗値 | 独立性の検定・適合度検定 |
これらを見ると、検定の名前と検定統計量が同じであることがわかりますね。
では次に、「なぜ検定統計量を使わなければならないのか」という理由をお伝えします。
検定統計量を使う理由は?P値との関係

仮説検定では、「ある事象が生じる確率」が事前に定めた有意水準以下の場合、帰無仮説を棄却し、対立仮説を採用するという流れです。
例えば、コイン投げやくじ引きでは「ある事象が生じる確率」を実際に計算することができます。
そのため、計算した確率と有意水準を比較することで仮説の検定を行うことができます。
しかし、テストの点数、体重や薬の効果などを対象にする場合、データからその値が生じる確率を直接計算することはできません。
そのため、テストの点数は偏差値に、体重や薬の効果などのデータも、取りうる値の確率を計算するために確率密度分布に変換する必要があります。
検定統計量は、様々なデータを確率密度分布に変換することで、検定で利用しやすくした統計量です。
検定統計量に変換することで、簡単に確率を求めることができるようになります。
検定統計量は、様々なデータを確率密度分布に変換することで、検定で利用しやすくした値のこと。
ただ、検定統計量は用いる検定によって変わってきますので、データから検定統計量への変換はこの記事では具体的な計算は取り上げません。
検定統計量と棄却域とP値
データから検定統計量を計算した後は、仮説検定を行うために棄却域を考えます。
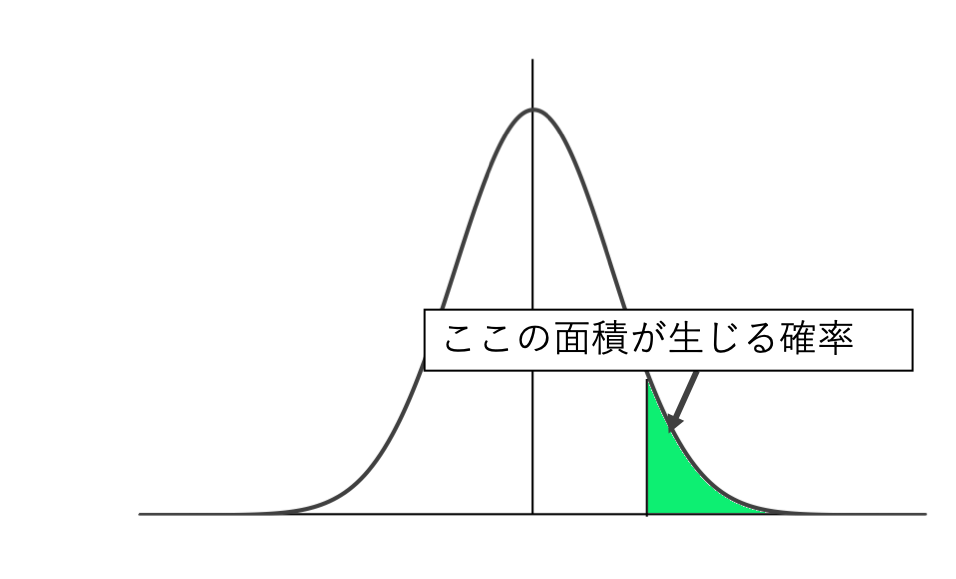
上の図はT検定におけるT分布を例にしたものです。
検定で用いる確率密度関数において、面積=確率でしたね。
有意水準が5%のときは、面積が0.05となる範囲が有意水準となります。
有意水準の考え方は以下の記事で説明しています。
>>>>有意水準と有意差とp値とは?5%の意味や決め方・求め方をわかりやすく簡単に
棄却域は有意水準を満たす範囲で、面積=有意水準となる横軸の範囲(域)を意味します。
有意水準が5%のときは、面積が0.05以下であれば、帰無仮説は棄却されます。
この域に計算した検定統計量があれば、帰無仮説を棄却するというルールでしたので、棄却域と呼びます。
棄却するかどうかの2つの判断方法とP値
棄却の判断は、有意水準との比較でおこないます。
正確には、検定統計量をとりうる確率と有意水準の比較で判断します。
そして、検定統計量をとりうる確率をP値と呼ぶのです。
そのため、検定統計量とP値は本質的には同じことを示しているもの。
となると、棄却の判断には2つの考え方があります。
- 検定統計量そのものから、有意水準と一致する検定統計量を比べる。
- 検定統計量から一度P値に変換し、P値が有意水準以下かどうかを調べる。
検定統計量とP値は本質的には同じことを示しているので、どちらでもいいのです。
ですが前者の方法には、短所があります。
それは、検定統計量は検定の種類(T検定やカイ二乗検定など)によって異なるため、検定について詳しく知っていないと大小関係の意味するものが変わるというものです。
面倒ですよね。
そのため、一般的には検定統計量がらP値を計算し、有意水準と比較する方法がよく用いられます。
どんな検定であれ、P値というものに変換さえすれば、あとは結果の見方が一律になります。
もし検定統計量がマイナスになったとき
検定統計量がマイナスになったとしても問題はありません。
先ほども述べたように、検定統計量は検定によって異なるためマイナスが出ても気にすることは基本的にないです。

前述の通り、上の図はT検定におけるT分布を例にしたものでした。
上記の例ではグラフの頂点である0よりも右側の面積を考えているため、t値はプラスであることを考えていました。
しかしT分布は0を真ん中にして左右対称の分布のため、マイナスになることも自然なことです。
下記の結果はEZRで共分散分析を実施した結果ですが、t値がマイナスになっていることがわかります。
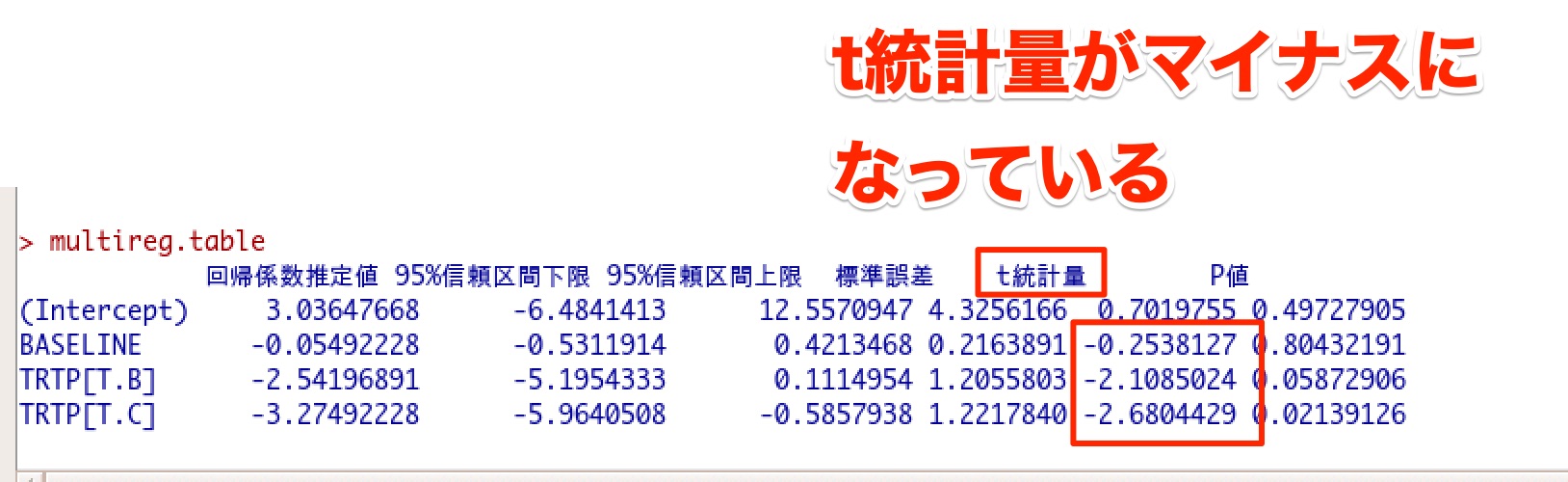
検定統計量がマイナスでも、落ち着いて、検定統計量をもとに計算したP値を計算しましょう。
まとめ

検定統計量は、データを確率密度関数に変換して、比較しやすくした値のことです。
検定統計量から最終的にP値を算出することで、検定の種類は違えど、最終的にはP値という一つの指標で全ての比較ができるようになります。
統計に関するご質問があれば、メルマガにご登録の上ご質問くださいませ!











コメント