この記事では「ロジスティック回帰における判別的中率(判別精度)とは?EZRでの算出法も」ということでお伝えさせていただきます。
- ロジスティック回帰における判別的中率とは?
- 判別的中率に基準はある?
- EZRで判別的中率を算出する!
ということをお伝えしますので、診断研究などで使われることもある判別的中率に関してマスターしましょう!
ロジスティック回帰における判別的中率とは?
まず判別的中率は、予後予測を目的とする研究で用いることがある指標です。
一言で言うと、統計モデルで推定された結果が、どれだけ正確に分類できたかの指標。
ですがあまりイメージできないかもしれませんので、具体的に分割表で示していきますね。
判別的中率は真陽性と真陰性を足した数の割合
判別的中率を数式で示すと、下記のようになります。
判別的中率 = (正確に分類されたサンプル数) / (全体のサンプル数)
つまり、下記のように「得られているデータ(実測値)」と「モデルからの予測」の分割表を作成したときに、黄色でマーカーした真陽性と真陰性を足した数の割合、ということになります。
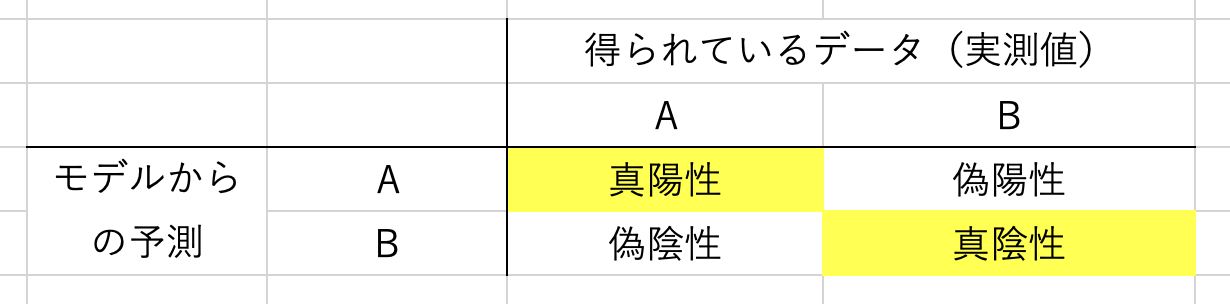
- 真陽性:実測値がAの場合に、モデルからの予測で正しくAと予測した場合
- 真陰性:実測値がBの場合に、モデルからの予測で正しくBと予測した場合
を指します。
全体の数に対して、真陽性と真陰性の2つを合わせた数の割合が判別的中率(判別精度)ということです。
判別的中率はロジスティック回帰分析とセットで使われることも多い
判別的中率は、ロジスティック回帰分析とセットで使われることも多いです。
なぜなら、ロジスティック回帰はアウトカムが2値のデータに適用する解析だから。
実測値の値(2値のデータ)はある状況で、モデルから予測値を算出すれば上記の分割表を作成可能になるためです。
判別的中率に基準はある?
復習までに、判別的中率は以下の定義です。
判別的中率 = (正確に分類されたサンプル数) / (全体のサンプル数)
上記の定義から、判別的中率は0~100%の値を取ることがわかります。
じゃあ、判別的中率はどれぐらいあるといいモデルと言えるのか!?と疑問に思うかと思います。
回答としては、基準値は特に明確にはないが、印象としては70~80%はほしいな、という印象。
株式会社アイスタットさんの解説によると、下記のような記載がありますので、やはり70~80%は必要なんじゃないかなとは思います。
判別的中率はいくつ以上あればよいという統計学的基準は有りませんが, 著者は75 % 以上あれば関係式は予測に適用できると判断しています。
EZRで判別的中率を算出する!
判別的中率のことが理解できたところで、実際にEZRで判別的中率を算出してみましょう!
今回はEZRのHPにあるサンプルデータの「Eye.rda」を使っていきます。
(こちらにあるデータ:https://www.jichi.ac.jp/saitama-sct/SaitamaHP.files/sample.html)
下記のようなデータになっていますので、疾患の有無(Disease)を性別(Sex)とグレード(Grade)で予測するモデル作成していきます。
EZRで実践する手順は4つです。
- ロジスティック回帰分析をする
- 予測値をデータに保存する
- 予測値から0と1のデータを作る
- 分割表を作って判別的中率を計算する
EZRで判別的中率を算出する手順その1:ロジスティック回帰分析をする
まずはEZRでロジスティック回帰分析を実施します。
統計解析 > 名義変数の解析 > 二値変数に対する多変量解析、を選択します。
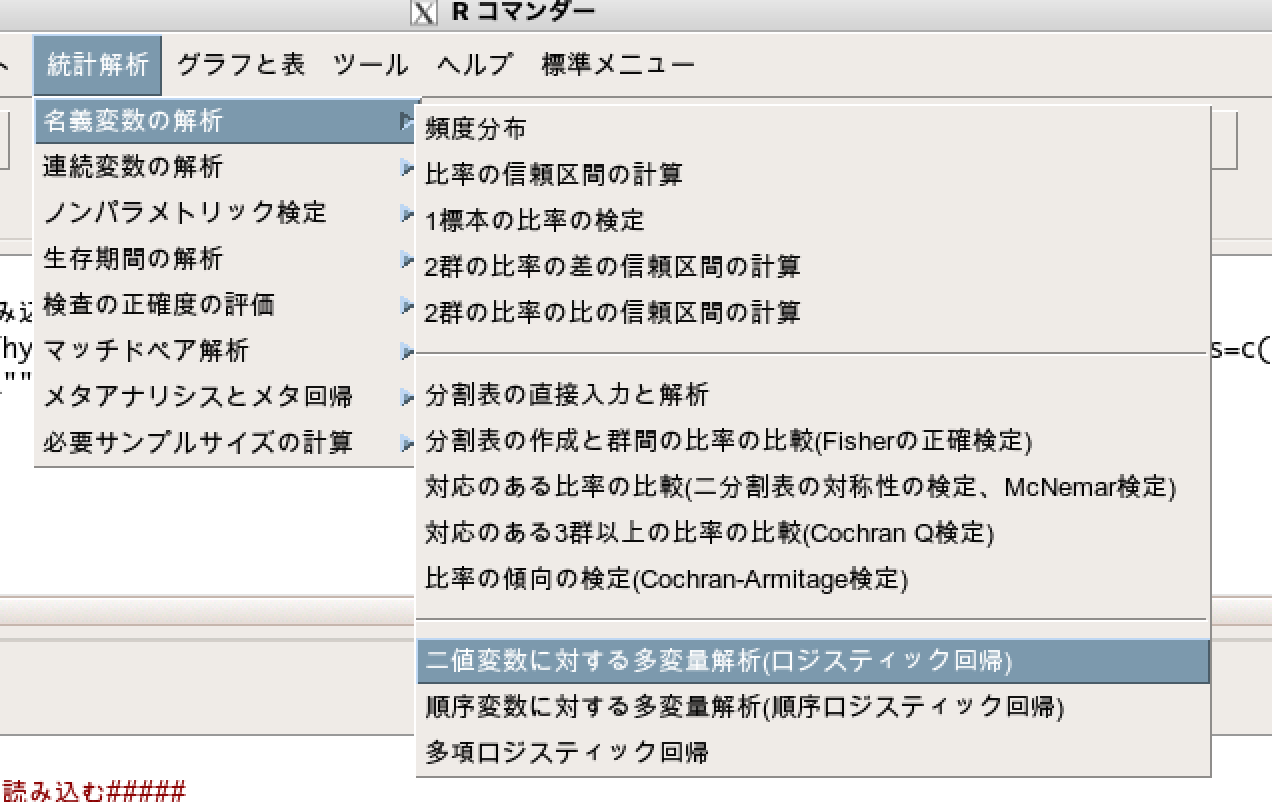
そして、説明変数と目的変数を指定します。
このとき、モデル名を覚えておくようにします。
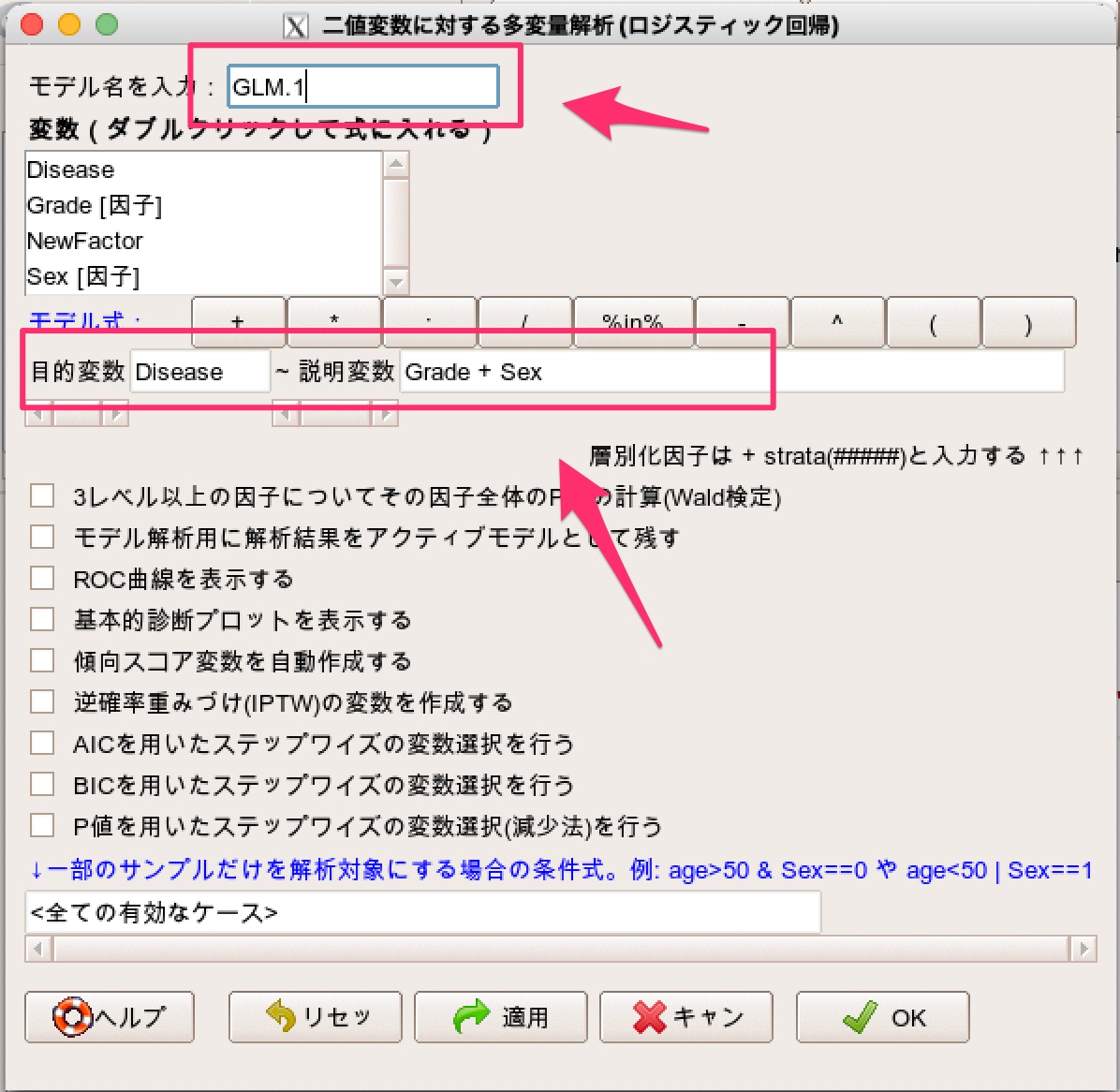
OKを押して実行すると解析結果が出力されます。
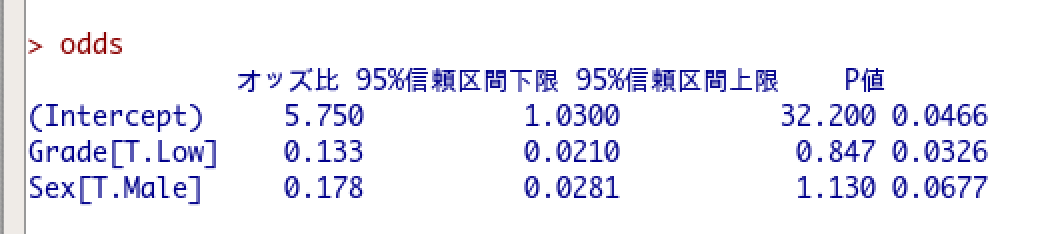
これで手順1はOKです。
EZRで判別的中率を算出する手順その2:予測値をデータに保存する
次に、データセットに対して予測値を保存します。
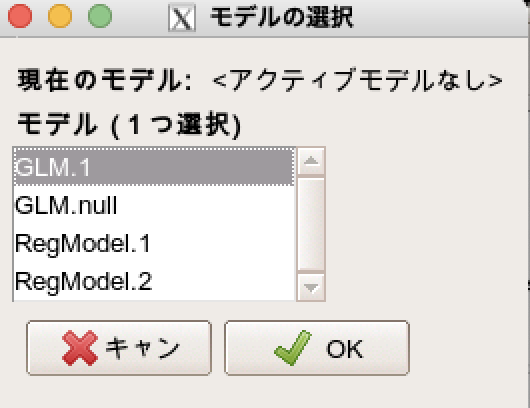
先程実施したロジスティック回帰のモデルを選択していきます。(標準メニュー > モデル > アクティブモデルを選択)
先程のGLM.1を選択します。
予測値をデータセットに格納させたい ので、標準メニュー > モデル > 計算結果をデータとして保存、を選択します。
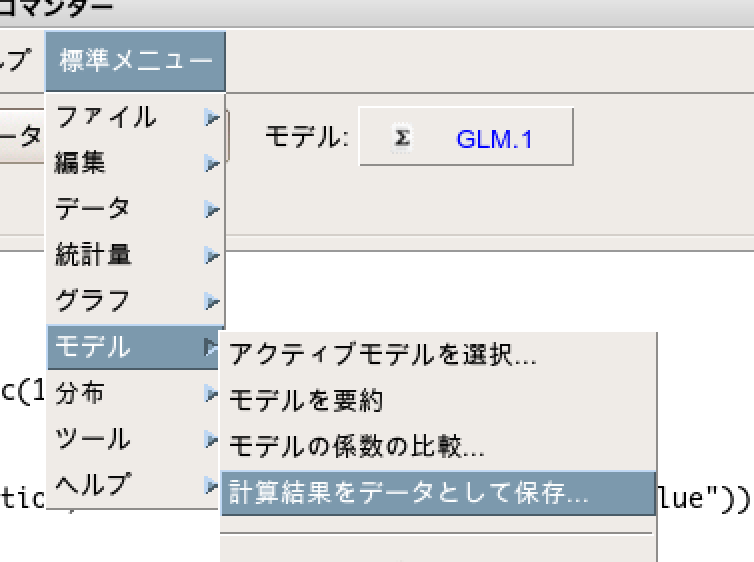
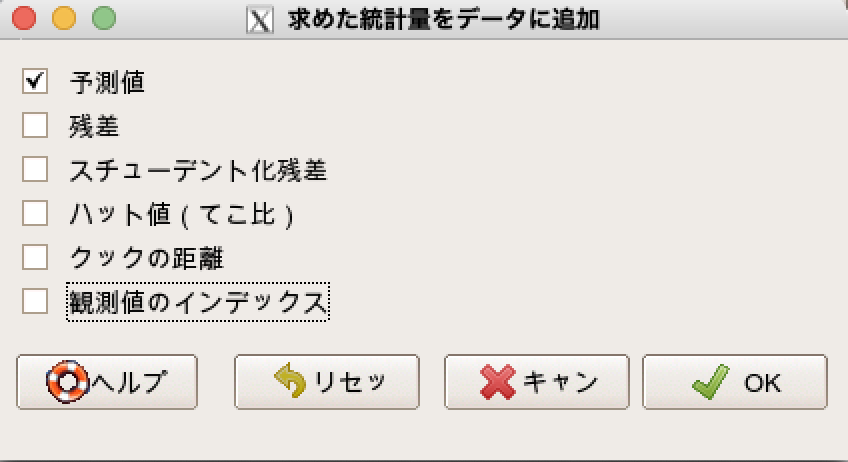
そうすると下記のようなウインドウが立ち上がりますので、予測値にチェックしてOKを押します。
その後、データセットを確認すると予測値(fitted.GLM.1)が格納されていることがわかります。
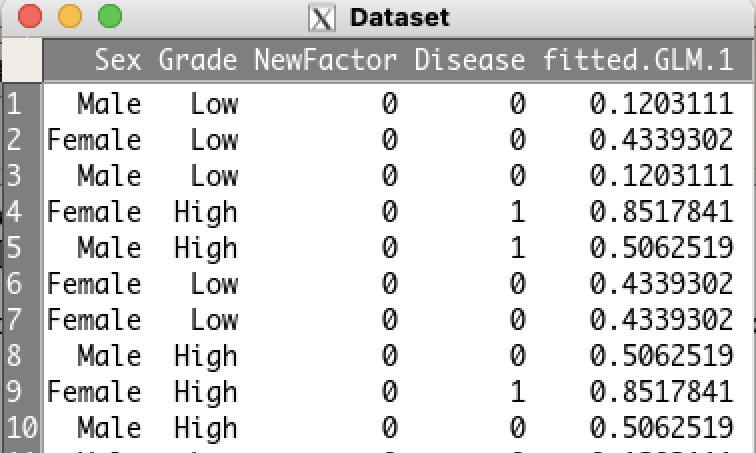
これで、手順2はOKです。
EZRで判別的中率を算出する手順その3:予測値から0と1のデータを作る
次に、予測値から0と1のデータを作ります。
予測値はまだ0〜1の実数になっているため、これを0と1に変換します。
具体的には、下記のプログラムをRスクリプトにコピペして実行します。
ただし、「GLM.1」の部分はモデル名に応じて要修正です。
Dataset$yosoku <- as.factor(as.numeric(Dataset$fitted.GLM.1>=0.5))
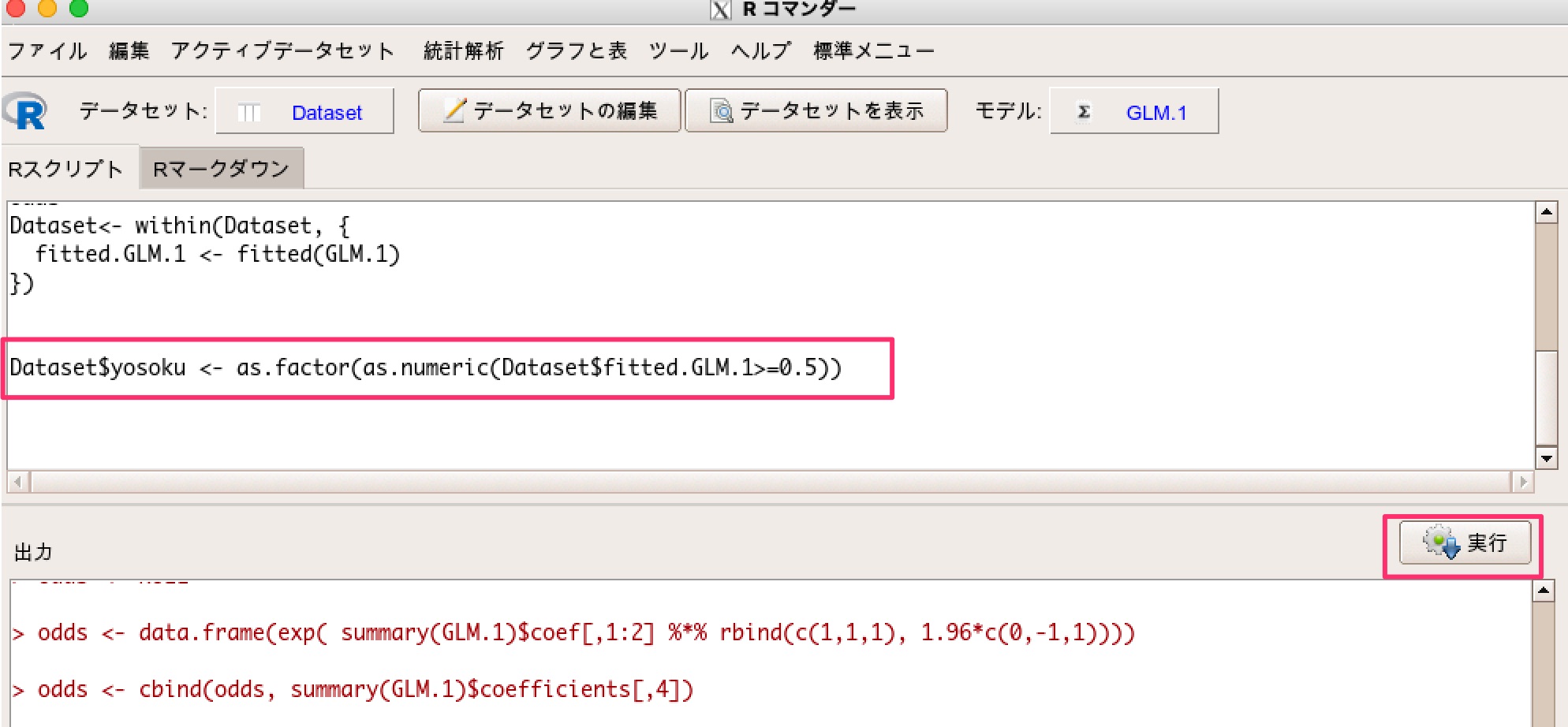
すると、データセットに0と1のデータであるyosokuの列ができます。
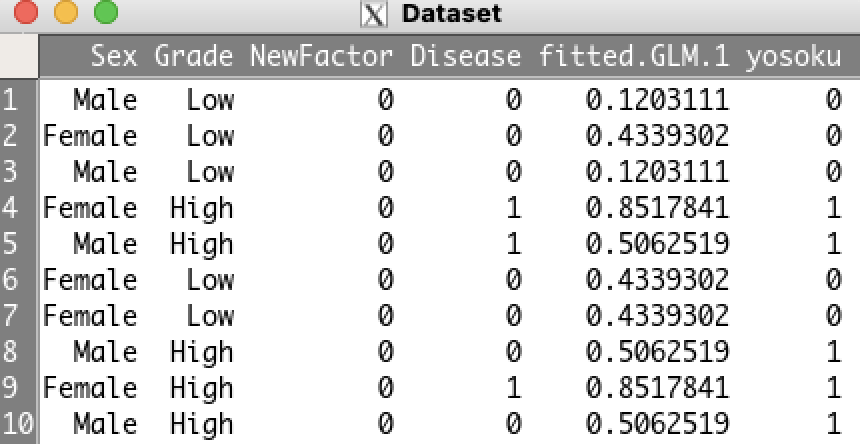
これで、手順3はOKです。
EZRで判別的中率を算出する手順その4:分割表を作って判別的中率を計算する
手順3までで、判別的中率を算出する準備が整いました。
つまり、実測値の0と1(Disease列)と予測値の0と1(yosoku列)が整った、ということです。
ここまでできたら、あとは分割表を作るだけ。
そのため、統計解析 > 名義変数の解析 > 分割表の作成、を選択します。
行にyosoku、列にDiseaseを選択して「全体のパーセント」を表示させるようにチェックを入れます。
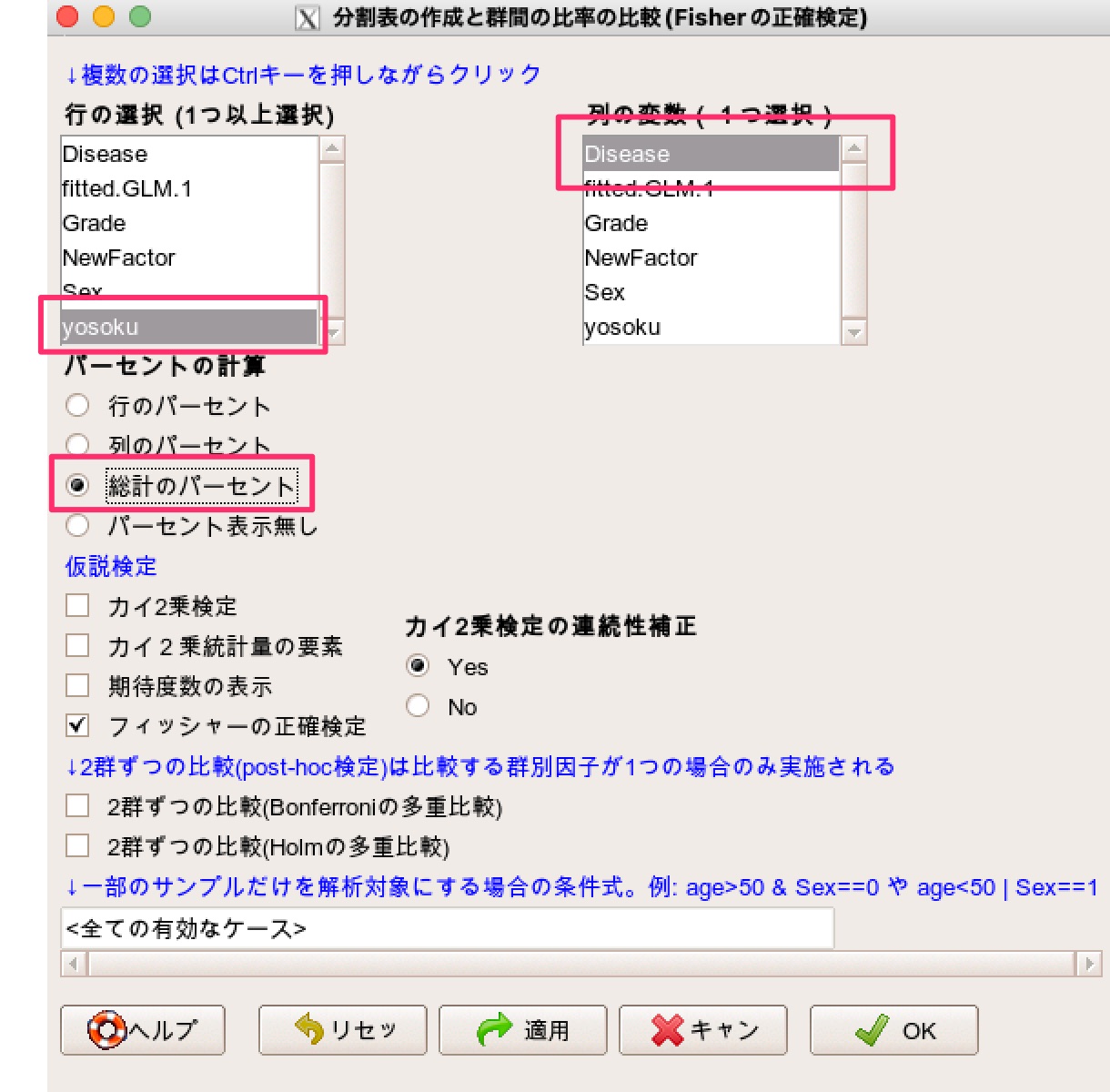
すると下記の結果が出てきますので、真陽性と真陰性のパーセントの足し算が判別的中率になります。
つまり、今回のデータでは39.3%+21.1%=71.4%が判別的中率になります。
この分割表のままですと95%信頼区間も出力できないため、念の為、統計解析 > 検査の正確度の評価 > 訂正検査の診断への正確度の評価、から確認していきます。
上記で得られた分割表の数値を入れます。
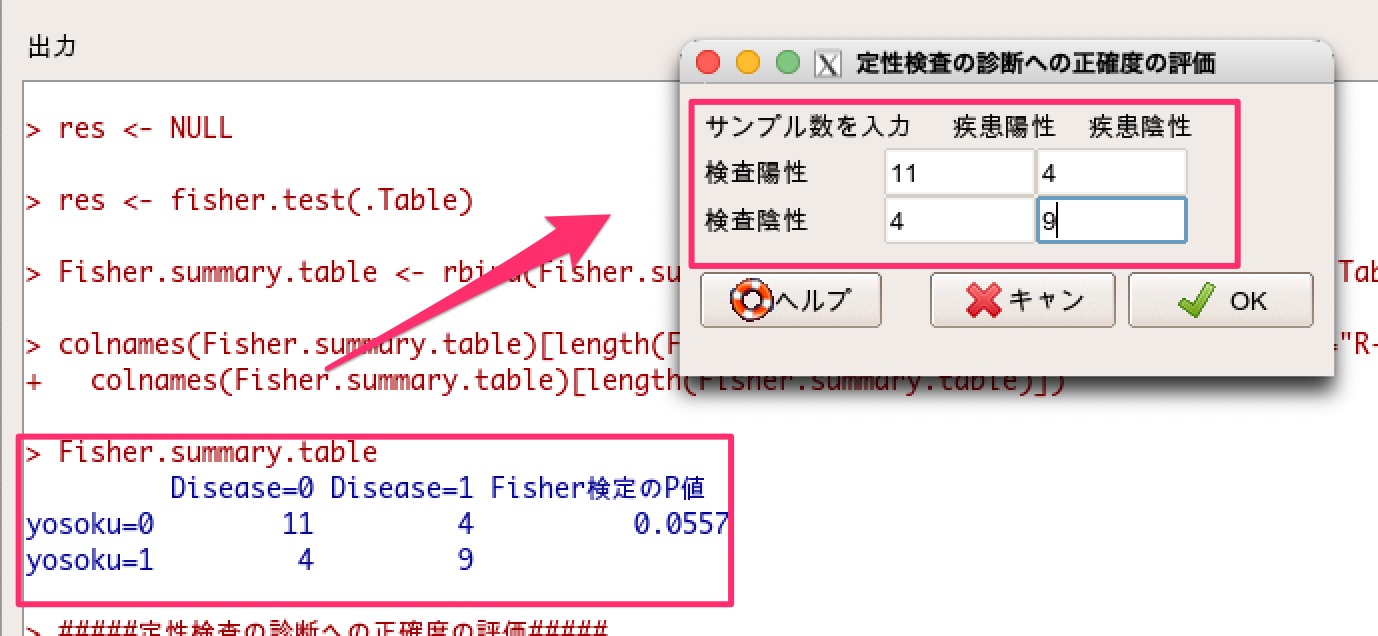
すると、判別精度という名前で、判別的中率と95%信頼区間が出力されます。

まとめ
いかがでしたか?
この記事では「ロジスティック回帰における判別的中率(判別精度)とは?EZRでの算出法も」ということでお伝えさせていただきました。
- ロジスティック回帰における判別的中率とは?
- 判別的中率に基準はある?
- EZRで判別的中率を算出する!
ということが理解できましたら、とても嬉しいです!
こちらの内容は動画でもお伝えしておりますので、併せてご確認くださいませ。













コメント