この記事では「ロジスティック回帰分析をわかりやすく!結果のオッズ比の見方・解釈・書き方も」ということでお伝えしていきます。
- ロジスティック回帰分析はどんな状況で使うの?
- なぜ「ロジスティック」回帰分析というのか?
- ロジット変換とは?
- ロジスティック回帰分析の結果の解釈はオッズ比が重要
といったことが理解できるようになりますよ!
ロジスティック回帰分析とは?どんな状況で使う?

まず、ロジスティック回帰分析を使う状況を整理します。
結論から言うと、ロジスティック回帰分析は「アウトカムが2値のカテゴリカル変数」の場合に使う解析。
カテゴリカル変数に対しての統計学的検定は「カイ二乗検定」と「フィッシャーの正確確率検定」の2つ。
ちょっとした変化球で、層別因子を考慮したい場合には「CMH検定」なんかもあります。
そんな質的データに対して単変量解析や多変量解析を実施したい、となったらロジスティック回帰というわけです。
(前向き研究限定ですが、ポアソン回帰も適用可能です。)
2値のカテゴリカルデータとしては「効いた/効いていない」とか「反応あり/反応なし」とか「イベントの発生/非発生」など、必ず2つの値のどちらかした取り得ないデータである、ということです。
注意していただきたいのが、「アウトカム(目的変数)が2値データである」という点。
説明変数(独立変数)に関しては、2値データに限りません。説明変数は連続変数でも全く問題ないです。
ロジスティック回帰分析を使う目的は?
カテゴリカル変数を扱う場合に使えるロジスティック回帰分析。
ロジスティック回帰分析を使う目的は「発生率(発生割合)を推定する」といった時に使えます。
例えば「1日の喫煙本数が肺がんの発生率にどう影響する?」といった疑問に答えるには、ロジスティック回帰分析が最適、ということですね。
なぜ「ロジスティック」回帰というのか?ロジット変換の意味

ロジスティック回帰分析の適用状況はわかりました。
ではなぜ、「ロジスティック」という言葉がついているのでしょうか。
それはロジスティック回帰分析が「ロジット変換」という変換を使っているからです。
発生割合を推定するときの問題点
ロジスティック回帰分析は「発生率(発生割合)を推定する」ときに使えます。
そして割合(確率)の基本的な前提ですが、割合(確率)は0〜1の間を取る、ということです。
発生割合が40%です、といった場合には、全体を1とした時に0.4です、ということです。
発生割合が1を超えることもないし、0より小さいマイナスの値を取ることもない。
これはなんとなくわかると思います。
でも、普通に回帰分析してしまうと、値が-∞から∞を取ることになってしまうんです。
これは結構重要な問題です。
発生割合に対しての推定結果が15(1500%)です、と言われても、そんな結果は無意味になってしまう。
なので、その問題点を解決するのにロジット変換が必要になってくるのです。
ロジット変換を行うことで、値が-∞から∞を取るものに変換することができ、問題点を解決することができるからです。
ロジット変換とは?
じゃあその重要なロジット変換。
定義は以下の通りです。

この変換の定義は「こんなもんだ」と覚えてもらうしかありませんね。
こういった変換のことをロジット変換と言うのです。
そして注釈にも記載しましたが、pは発生割合であり、1-pは非発生割合です。
ということは、p/(1-p)ってなんでしたでしょうか?
そう、オッズです。
ロジット変換とは、言い換えればオッズを対数化したもの。
そしてA群のオッズとB群のオッズを比較する方法がオッズ比ですので、ロジスティック回帰分析の結果をちゃんと解釈できるようになるには、オッズ比の知識が重要になります。
ロジスティック回帰分析の結果はオッズ比を見る

ロジスティック回帰分析が何かを整理できたところで、結果の見方に関して見ていきましょう。
ロジスティック回帰分析はかなりメジャーな解析ですので、無料の統計ソフトEZRでも問題なく実施することが可能です。
そして上述の通り、ロジスティック回帰分析のメインの結果はオッズ比です。
例えばEZRで実施すると、下記のような結果が出力されます。
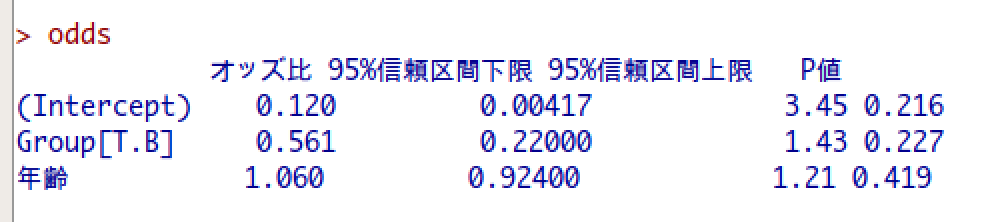
オッズ比の推定値とその95%信頼区間が出力され、P値も出力されています。
そのため、ロジスティック回帰分析の結果を解釈するために、オッズ比をちゃんと理解しておきましょう!
そして、統計解析ソフトによっては「オッズ比」という言葉が出てこない時もあります。
下記の結果はSPSSでロジスティック回帰分析を実施した結果。
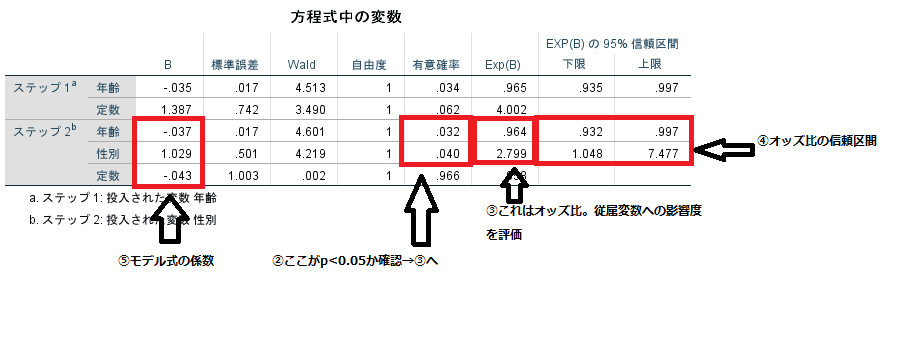
どこにもオッズ比という言葉がないですよね。
でもロジット変換のことを理解していればなんとなく見当はつくのですが、Exp(B)というところがオッズ比を示しています。
ロジット変換で対数化(log)しましたので、それを戻すには指数化(exp)します。
オッズ比の見方・解釈・論文への書き方は?
ロジスティック回帰分析を実施すると、最終的にはオッズ比が結果として得られることがわかりました。
もう一度、EZRで出力されるオッズ比の結果を見てみましょう。

GroupはA群とB群という2群の情報が入ったカテゴリカル変数で、年齢は連続変数(単位:歳)です。
カテゴリカル変数も連続変数も、どちらにもオッズ比が出力されていることがわかります。
重要なのが、このオッズ比の解釈ですよね。
オッズ比の解釈は、カテゴリカル変数と連続変数では若干違いがあります。
ロジスティック回帰分析でカテゴリカル変数が説明変数の場合のオッズ比の解釈
まずはカテゴリカル変数が説明変数の場合。
カテゴリカル変数が説明変数の場合、必ず「参照群(Reference)」となる群が1つ指定されます。
上記のA群とB群のGroupの場合、A群が参照群となり、参照群に対して他方の群(B群)の結果が出力されています。
つまり、参照群(A群)に対する、他方の群(B群)の結果が出力されているのです。
今回の場合、Group[T.B]のオッズ比が0.561のため「A群に比べてB群の方がアウトカムを発生させにくい」という解釈になります。(p値の解釈は無視しています。)
ロジスティック回帰分析で連続変数が説明変数の場合のオッズ比の解釈
次に、連続変数が説明変数の場合。
この場合は「1単位上昇した場合にオッズ比がどう変化するか」という結果が出力されます。
年齢であれば「1歳上昇した場合にオッズ比がどう変化するか」という意味です。
身長(cm)だったら「1cm上昇した場合にオッズ比がどう変化するか」という意味です。
今回の場合、年齢のオッズ比が1.06のため「年齢が上昇するとアウトカムを発生させやすい」という解釈になります。(p値の解釈は無視しています。)
ロジスティック回帰分析をした後の結果の記載方法は?
ロジスティック回帰分析をした場合のオッズ比の結果の解釈が理解していただけたかなと思います。
最後に、論文などへの結果の記載方法です。
結論から言えば、「オッズ比、オッズ比の95%信頼区間、p値」の3点セットを付与すればOKです。
決して「オッズ比だけ」とか「p値だけ」という結果の記載はNGですので、ご注意ください。
まとめ

いかがでしたか?
この記事では「ロジスティック回帰分析をわかりやすく!手順や結果のオッズ比も解説」ということでお伝えしました。
- ロジスティック回帰分析はどんな状況で使うの?
- なぜ「ロジスティック」回帰分析というのか?
- ロジット変換とは?
- ロジスティック回帰分析の結果の解釈はオッズ比が重要
といったことが理解できたのなら幸いです!
こちらの内容は動画でも解説していますので、併せてご確認くださいませ。














コメント
コメント一覧 (2件)
[…] ロジスティック回帰分析 […]
[…] […]