この記事では「クロスオーバー試験の統計解析をわかりやすく!並行群間比較試験との違いは」ということでお伝えしていきます。
クロスオーバー試験(クロスオーバーデザイン)って耳にしたことがあるけど、具体的にどんな目的で使われているのか、なかなか分からなかったりしますよね。
また、現時点でクロスオーバーデザインのデータがあるんだけど、統計解析しろと言われたら全くもってどうすれば良いのかわからない、、、という悩みを持っている方もいるかなと。
ということで本記事では
- クロスオーバー試験とは?並行群間比較試験との違いは?
- クロスオーバー試験で注意すべき持ち越し効果と時期効果
- JMPとSPSSでクロスオーバー試験の統計解析を実施してみる
ということでお伝えしていきますね!
クロスオーバー試験とは?並行群間比較試験との違いは?

まずはクロスオーバー試験の特徴を整理していきましょう。
クロスオーバー試験(2*2クロスオーバーデザインの場合)を視覚的に表示すると、以下ののようになります。
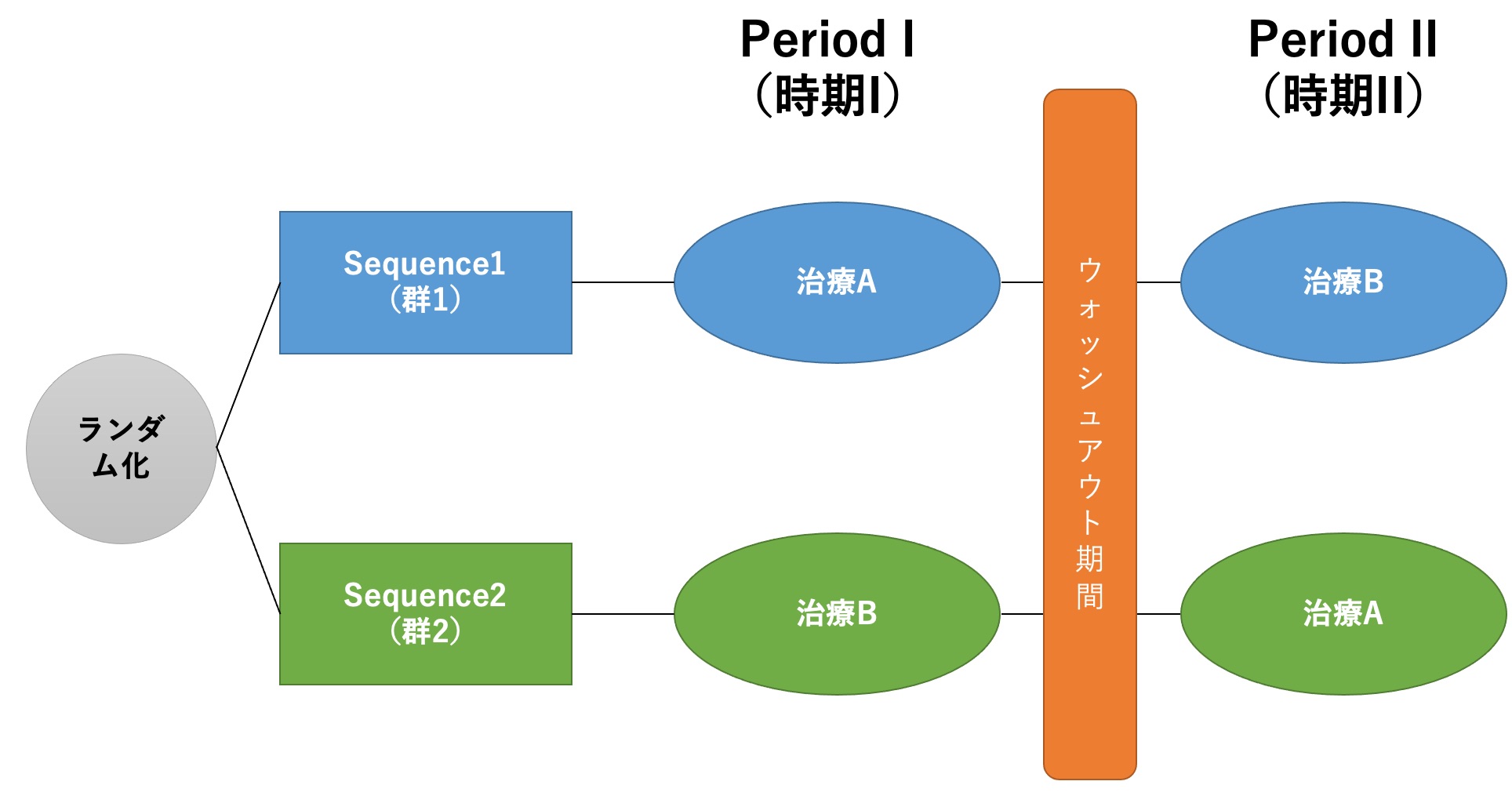
一番の特徴はなんといっても、「1人の被験者が2つの介入を受ける」ということ。
並行群間比較試験であれば、「1人の被験者は1つの介入を受ける」ですから、そこが一番の違い。
クロスオーバー試験もランダム化比較試験の一つですが、治療に対してランダム化するのではなく、どっちの治療をどの順番で受けるか(Sequence)に対してランダム化するのが特徴的です。
クロスオーバー試験のメリットデメリット
「1人の被験者が2つの介入を受ける」というのが特徴的なクロスオーバー試験。
この特徴により、メリットとデメリットが発生します。
クロスオーバー試験の最大のメリットは、症例数を削減できること。
むしろ、このメリットだけで採用される試験デザインかもしれません。
なぜ症例数を削減できるかと言えば、「1人の被験者が2つの介入を受ける」ということで、単純な話で言えば、集める症例数は半分ぐらいで良さそうですよね。
それにプラスして、個人内のばらつきを考慮できるため、並行群間試験よりもデータのばらつきが小さくなることを期待できるから。
「今日の私の血圧と1ヶ月後の私の血圧」の方が、「今日の私の血圧と1ヶ月後の他の誰かの血圧」よりもばらつきは小さいはず。
なので、個人間のばらつきだけを考慮しなければならない並行群間比較試験よりも、個人内のばらつきを考慮できるクロスオーバー試験の方が、ばらつきが小さくなることが期待できます。
ではクロスオーバー試験のデメリットはなんでしょうか。
最大のデメリットは解析の複雑性です。
解析の仕方は後述しますが、「時期効果」や「持ち越し効果」なんかを考えなければいけないため、解析方法やデータの整理が複雑になります。
クロスオーバー試験で注意すべき持ち越し効果と時期効果

クロスオーバー試験を採用することによって、考慮しなければならないことがあります。
それは下記の3つ。
- 持ち越し効果
- 時期効果
- 治療効果
それぞれ解説していきます。
持ち越し効果とウォッシュアウト期間
持ち越し効果とは、時期Iの効果が時期IIまで持ち越されること。
例えばSequence1では、時期Iに治療Aを実施され、時期IIに治療Bを実施されます。
仮に治療Aの効果が持ち越されてしまうと、時期IIのデータは「治療B+治療Aの持ち越し分」になってしまいます。
そのため、持ち越し効果は無くすように努力することが大切です。
薬剤開発でクロスオーバー試験を使う場合には、半減期の5倍以上の期間を空けることが推奨されています。
これを「ウォッシュアウト期間」と呼んでいますね。
なぜ半減期の5倍以上かと言えば、1/2の5乗を計算すると、0.03程度の薬剤しか体内に残らないと計算できるからです。
0.03程度であれば、ほぼ薬剤の効果はないよね、とみなせるからですね。
時期効果
時期効果とは、時期Iと時期IIの違いにより生まれる効果、ということです。
例えば、時期Iは夏で時期IIは冬だったとすると、気温の違いがもしかしたらデータに違いを生じさせるかもしれません。
人によって治療A(治療B)を受ける時期が違うので、考慮しなければならないですよね。
なので基本的に時期効果はないことを期待します。
治療効果
治療効果は、治療Aと治療Bの効果の違いのことを指します。
本来検証したいことは、この治療効果なはず。
この治療効果を正しく推定するために、持ち越し効果や時期効果がないように努力して試験デザインを考えたり、解析したりする必要があるのです。
JMPとSPSSでクロスオーバー試験の統計解析を実施してみる

クロスオーバー試験の大枠が整理できたところで、実際にJMPとSPSSとRでクロスオーバー試験の解析を実施してみたいと思います。
参考となるファイルとしては、富山大学の折笠先生が公開されているこちらのPDFを参考にさせていただきます。
繰り返しになりますが、クロスオーバー試験の場合には「時期効果や被験者効果なども考慮しながら治療効果を推定する」ということが重要になります。
そのため、データとしては群(Sequence)、治療の種類(A,B)、時期(Period)の変数を作成する必要があります。
想定する回帰分析の統計モデルは以下の通りです。
- 目的変数:FEV
- 説明変数(4つ):Sequence、治療の種類、時期、被験者(Sequence)を変量効果として入れる
データは富山大学の折笠先生が公開されているこちらのPDFの表3にあるデータ。
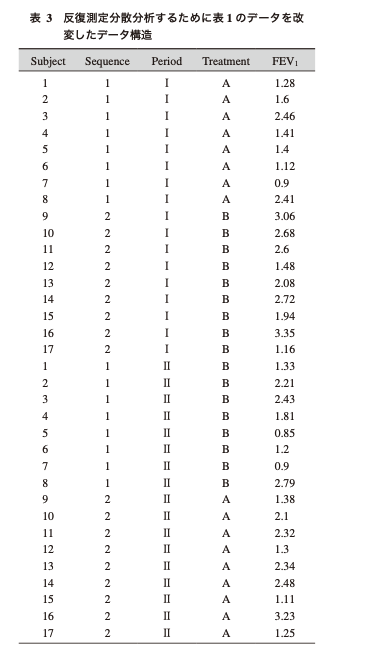
そして解析結果は以下の通りになるはずなので、JMPでもSPSSでもTreatmentがP=0.0472になることを目指します。
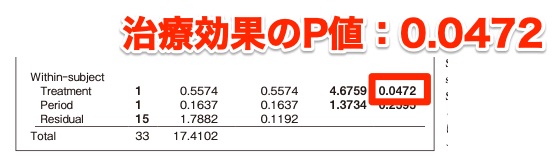
JMPでクロスオーバー試験の統計解析を実施
JMPでクロスオーバー試験の統計解析を実施してみます。
データは上述の通り、表3の通りにまとめておきます。
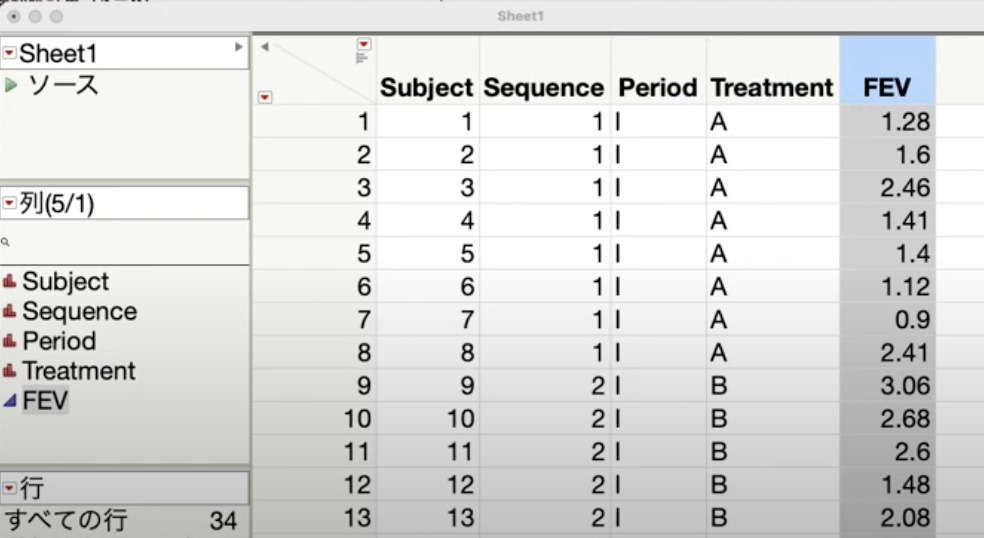
そして「分析」>「モデルの当てはめ」を選択し、以下のように変数を選択します。
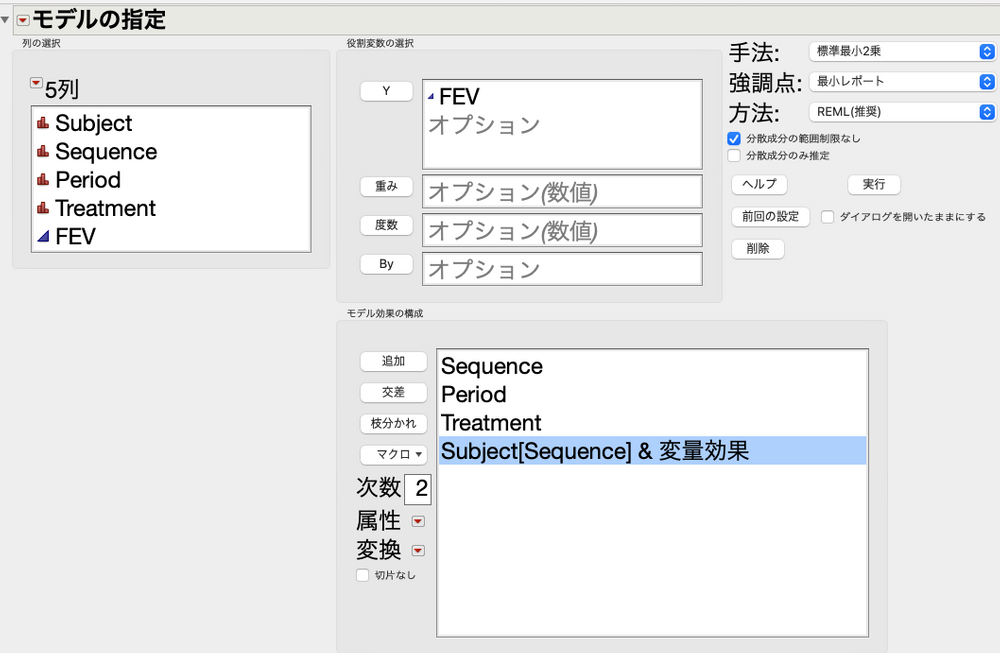
Subject[Sequence] & 変量効果、という変数を作るには、以下の手順で実施します。
- Subjectをモデル効果の構成に入れる
- モデル効果の構成に入っているSubjectと左上にあるSequenceをどっちも選択した状態で「枝分かれ」をクリックする
- するとSubject[Sequence]になるため、Subject[Sequence]を選択し「属性」の赤い三角形を押して変量効果に指定する
これでSubject[Sequence] & 変量効果、という変数を作ることが可能です。
この状態ができたら、「実行」を押します。
すると、以下のような解析結果が出力されることに。
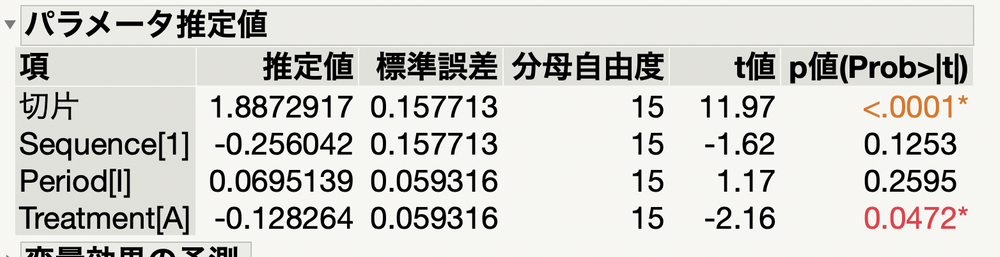
TreatmentのP値が0.0472であることがわかるので、結果を再現できました。
SPSSでクロスオーバー試験の統計解析を実施
では次に、SPSSでクロスオーバー試験の統計解析を実施してみます。
データは上述の通り、表3の通りにまとめておきます。
「分析」>「混合モデル」>「線形」を選択します。
そして下記のように被験者にSubjectを選択します。
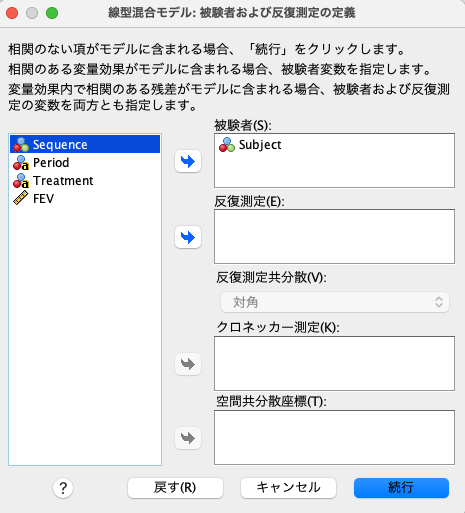
この状態で「続行」を押します。
そして下記のように、従属変数にFEVを選択、因子にSubject、equence、治療の種類、時期の4つの変数を選択します。
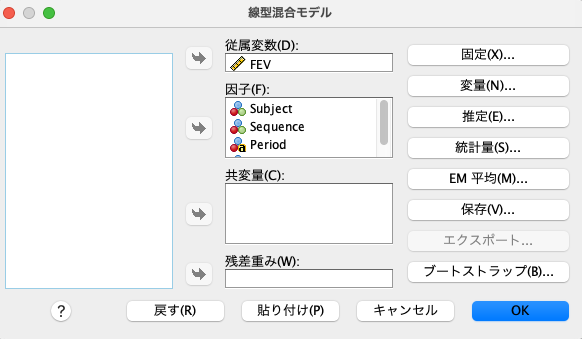
その次に、「固定」を押して、Sequence、治療の種類、時期の3つの変数を選択して主効果として含めます。
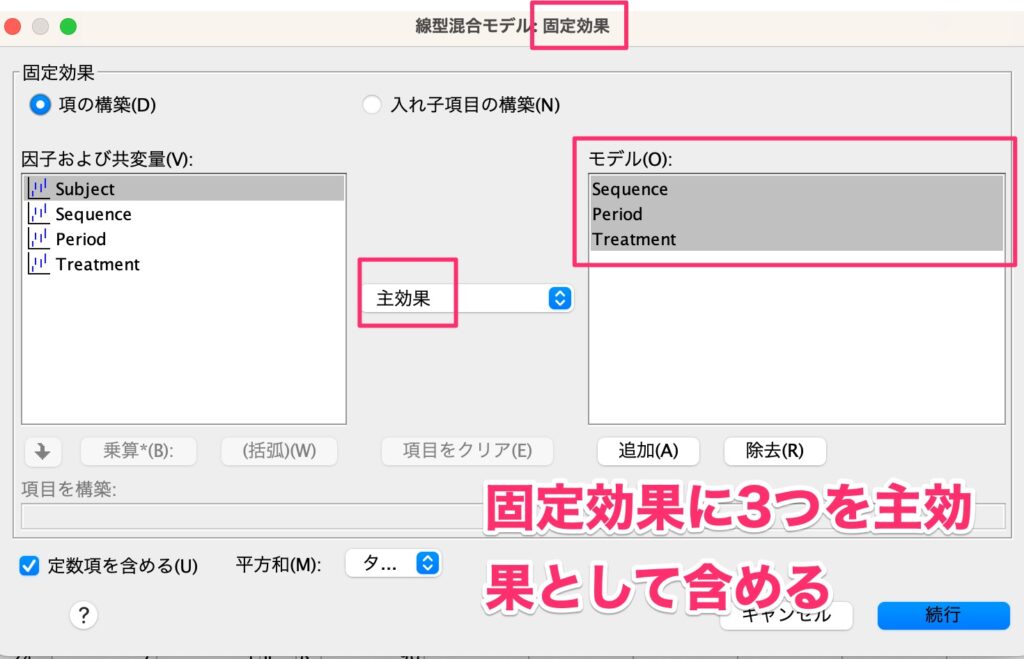
それから、Subject[Sequence] は変量効果として入れたいため、「変量」を押します。
Subject[Sequence] は「入れ子の項目」なので、以下の手順で作成します。
- 「入れ子項目の構築」を押します。
- Subjectを選択し、↓を押します。
- 「括弧」を押します。
- Sequenceを選択し、↓を押します。
- するとSubject(Sequence)が作成されるため、「追加」を押します。
統計量から、「記述統計」と「固定効果のパラメータ推定値」を選択します。
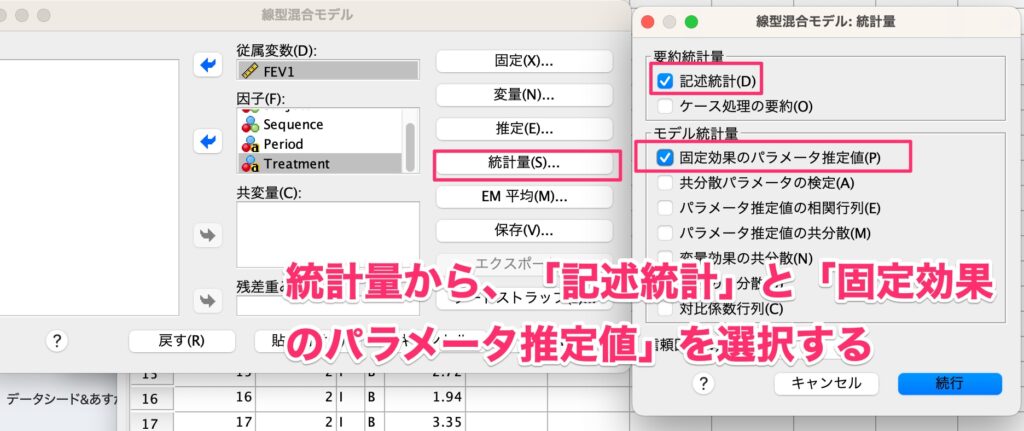
群間比較を目的としているため、EM平均でTreatmentを選択します。
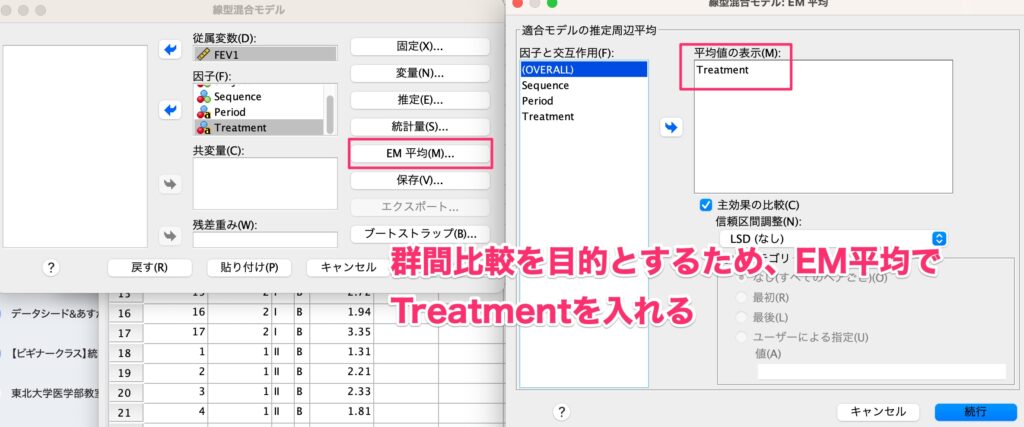
そうすると下記のように、変量効果としてSubject(Sequence)をモデルに含めることができます。
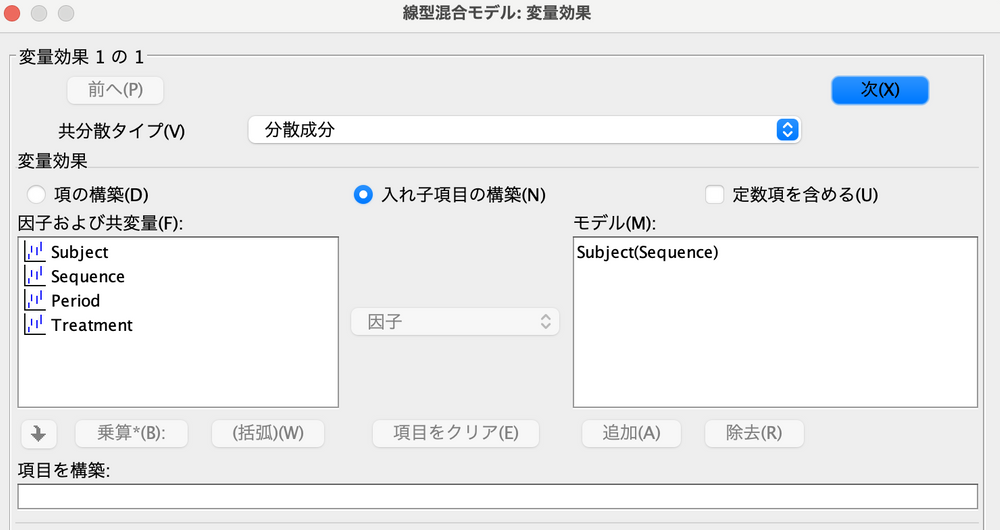
そして解析を実施すると、以下のような結果を得ることができます。
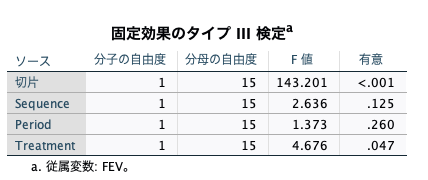
TreatmentのP値が0.047であることがわかるので、結果を再現できました。
また、Treatmentの最小二乗平均値は、A群が1.759、B群が2.016であることがわかります。

Rでクロスオーバー試験の統計解析を実施
では最後にRでクロスオーバー試験の統計解析を実施してみます。
データは上述の通り、表3のデータをRで作成するところから始めていきます。
#1度だけ実施する。過去にインストールしたことがあれば実行しなくてOK
install.packages("lmerTest")
# パッケージの読み込み
library(lmerTest)
# サンプルデータを作成する
sampledata_crossover <- data.frame(
PatientID = c(1,2,3,4,5,6,7,8,9,10,11,12,13,14,15,16,17,
1,2,3,4,5,6,7,8,9,10,11,12,13,14,15,16,17),
Sequence = c(1,1,1,1,1,1,1,1,2,2,2,2,2,2,2,2,2,
1,1,1,1,1,1,1,1,2,2,2,2,2,2,2,2,2),
Period = c("I","I","I","I","I","I","I","I","I","I","I","I","I","I","I","I","I",
"II","II","II","II","II","II","II","II","II","II","II","II","II","II","II","II","II"),
Treatment = c("A","A","A","A","A","A","A","A","B","B","B","B","B","B","B","B","B",
"B","B","B","B","B","B","B","B","A","A","A","A","A","A","A","A","A"),
Outcome = c(1.28,1.6,2.46,1.41,1.4,1.12,0.9,2.41,3.06,2.68,2.6,1.48,2.08,2.72,1.94,3.35,1.16,
1.33,2.21,2.43,1.81,0.85,1.2,0.9,2.79,1.38,2.1,2.32,1.3,2.34,2.48,1.11,3.23,1.25)
)
# データの表示
print(sampledata_crossover)
# 線形混合効果モデルの実行
fit <- lmer(
Outcome ~ Sequence + Treatment + Period + (1|PatientID/Sequence),
data = sampledata_crossover
)
# 結果の表示
anova(fit)上記のプログラムを実施すると、下記のような結果が出力されます。
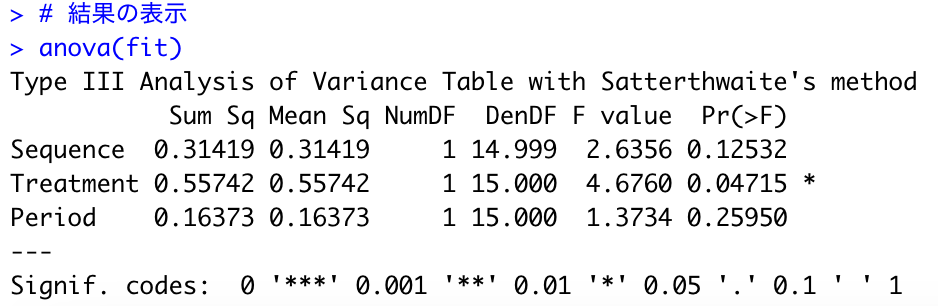
Treatmentのp値が0.04715(四捨五入で0.0472)となりましたので、結果を再現できました。
まとめ

いかがでしたか?
この記事では「クロスオーバー試験の統計解析をわかりやすく!並行群間比較試験との違いは」ということでお伝えしました。
- クロスオーバー試験とは?並行群間比較試験との違いは?
- クロスオーバー試験で注意すべき持ち越し効果と時期効果
- JMPとSPSSでクロスオーバー試験の統計解析を実施してみる
ということが理解できたのなら幸いです!













コメント