今日の記事は、マンホイットニーのU検定をEZRで実施する方法をお伝えします。
マンホイットニーのU検定はどんな検定だったか覚えていますか?
ウィルコクソンの順位和検定とやっていることは同じで、連続量を対象としたノンパラメトリック検定ですよね。
では、連続量を対象としたパラメトリック検定は?
そう、T検定です。
ということで、今回の記事はマンホイットニーのU検定をEZRで実施する方法に加えて、同じデータに対してT検定を実施した時の違いまで解説します。
EZRでマンホイットニーのU検定を実施するために必要となるデータを読み込む

まずは、マンホイットニーのU検定(以下、U検定)を実施するために必要なデータを解説します。
U検定は、2群の連続量を対象としたノンパラメトリック検定でした。
ということは、用意するデータは以下の2つを満たす必要があります。
- 連続量のデータが必要。
- 2群の群間比較をするので、2つのカテゴリを持つ、カテゴリカルデータが必要。
EZRでマンホイットニーのU検定を実施するのに使用するデータ
ということで、今回の記事で使うデータです。
今回はA群、B群の2つの群で、LDHの平均値を比較してみます。
(データは架空のデータです。)
実際には、T検定で実施したときと同じデータを使います。
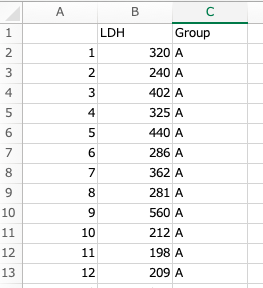
LDHが連続データで、Groupが群を示した変数です。
A群13例、B群11で、計24症例分のデータがあります。
EZRにU検定を実施する基となるデータを読み込む
ではここから、EZRにデータを取り込みます。
まずは、サンプルデータを適切な場所に保存しておきましょう。
EZRを開き、「ファイル」→「データのインポート」→「ファイルまたはクリップボード, URLからテキストデータを読み込む」を選択します。
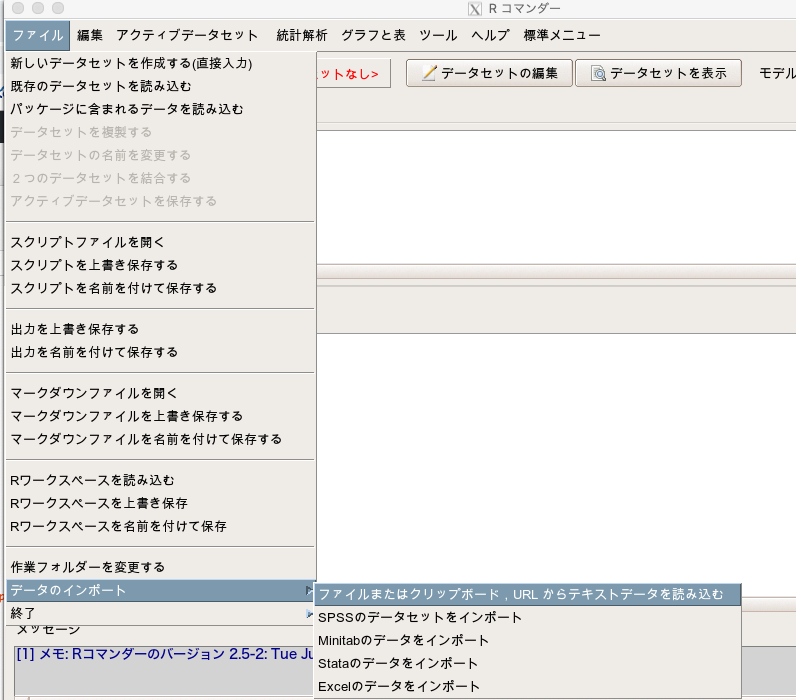
データセット名は「utest」にしましょう(実際はなんでもよい)。
そして「ローカルファイルシステム」と「カンマ」にチェックを入れてOKを押します。
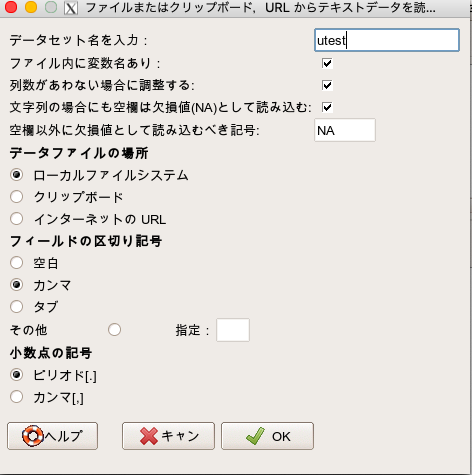
データセットが「utest」になっていることを確認し、「表示」を押してデータが正しく表示されれば取り込み完了です。
無料で使える統計ソフトEZRでマンホイットニーのU検定を実践する!
解析するための準備が整いましたので、早速U検定を実施してみましょう。
U検定を実施するには、以下の手順で行います。
「統計解析」→「2群間の比較」→「Mann-Whitney U検定」
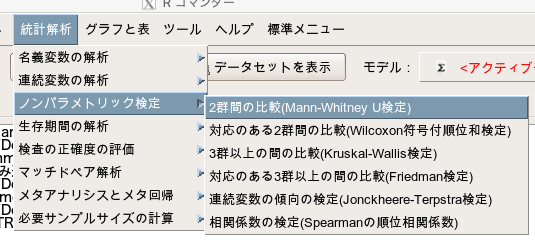
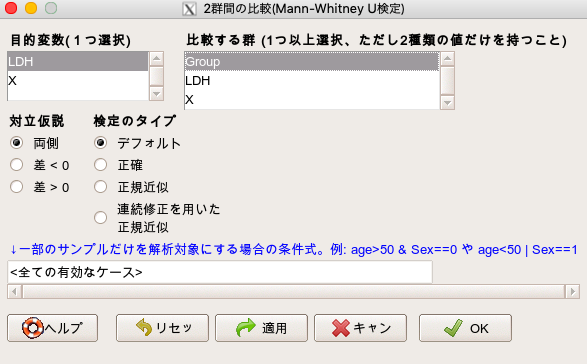
- 目的変数(1つ選択)で「LDH」を選択します。
- 比較する群(1つ以上選択)で「Group」を選択します。
- 対立仮説は「両側」を選択します。
- 検定のタイプは「デフォルト」でOKです。
- 他は、いじらなくてOKです。
これで解析を実行すると、以下の解析を自動で行ってくれます。
- マンホイットニーのU検定結果
- 各群のレンジ、四分位範囲、中央値などの要約
- 各群の箱ひげ図の作成
EZRで出力したU検定結果の解釈をしよう
実際にU検定が実施できました。
では、結果の解釈をしていきましょう。
U検定の結果解釈
まずはU検定の解析結果です。

まず、Wilcoxon rank sum testと書かれてあります。
「あれ、マンホイットニーのU検定じゃなかったっけ?」って思いますよね。
実は、マンホイットニーのU検定と、ウィルコクソンの順位和検定は同じことを実施しています。
そのため、ウィルコクソンの順位和検定の結果が出ていたとしても問題ないので、あわてないでおきましょう。
Data: LDH by factor(Group)とあります。
これは、GroupごとにLDHを比較したという意味です。
そして次の行にはp値が表示されています。
0.0138というP値を得られました。
0.05より小さいため、有意水準を0.05に設定していた場合には、有意差ありという結論になります。
次の行には対立仮説が表示されていますね。
「true location shift is not equal to 0」とあります。
ウィルコクソン検定は、連続量データを“順位”に変換して解析する手法でした。
そのため、対立仮説のlocation shiftというのは、“順位変動”と読み替えていただければ理解できますね。
各群の中央値と四分位範囲の結果解釈
その次に、各群の中央値と四分位範囲が要約されています。

箱ひげ図も出力される
設定の際に、グラフは「箱ひげ」を出力するようにチェックを入れたので、箱ひげ図が作成されています。
詳細は箱ひげ図の記事を参照していただきたいのですが、簡単に解説します。
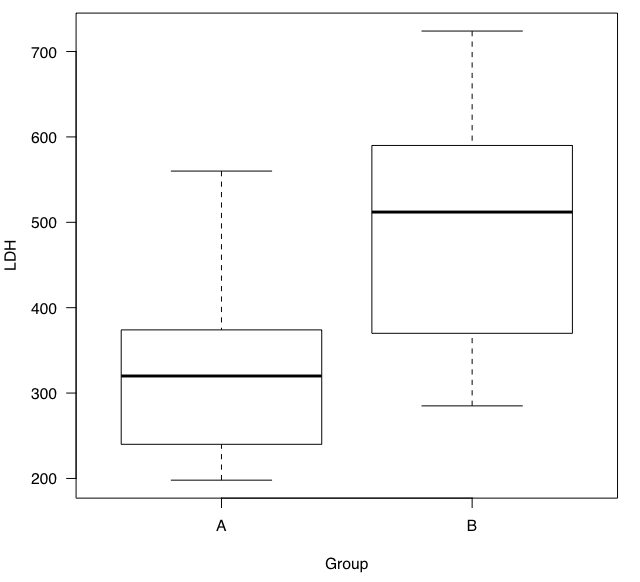
箱ひげ図は、箱の部分とひげの部分がある、かなり特徴的なグラフです。
箱が四分位範囲を示しています。
ひげは箱の1.5倍(それぞれ上側に1.5倍、下側に1.5倍の意味)の長さまでのデータの範囲を示しています。
ひげから外れたデータは、外れ値として示されています。
これを見るだけでも、データの分布がA群とB群で異なっていることが分かります。
同じデータでT検定を実施するとどうなるのか?
以上の手順で、マンホイットニーのU検定をEZRで実施することができました。
次なる疑問は、同じデータでT検定を実施すると結果はどうなるのか!?ということ。
今回はT検定を実施した際と同じデータを使用しましたので、P値を比較しましょう。
同じデータでT検定を実施すると、P=0.00496が得られていますね。
つまり、T検定の結果の方が、P値が小さいことが分かります。
T検定とU検定の検定結果の違いはこのような関係になります。
| データの分布 | T検定(パラメトリック) | ウィルコクソンの順位和検定(ノンパラメトリック) |
| 正規分布 | ◎ | ◯ |
| 正規分布ではない | × | ◯ |
今回のデータは正規分布に近かったという考察ができます。
本当に正規分布なのか!?ということを確認するために、ヒストグラムを作成してみましょう。
データが正規分布に近いのか、EZRでヒストグラムを作成する
ヒストグラムを作成するためには、「グラフと表」→「ヒストグラム」を選択します。
変数(1つ選択)で「LDH」を選択します。
群別する変数(0~1つ選択)で「Group」を選択します。
あとは、いじらなくてOKです。
すると、以下のようなグラフが作成されました。

A群もB群も、真ん中が一番大きい山になり、そこから左右対称に例数が小さくなっているように見えます。
ということで、視覚的にも正規分布に近い、ということが確認できました。
EZRでマンホイットニーのU検定まとめ

今回は、EZRでマンホイットニーのU検定を実施しました。
同じデータでT検定を実施すると、今回のデータではT検定のP値の方が小さくなっています。
ヒストグラムを確認するとデータが正規分布に近い形をしていたため、この結果には納得です。














コメント