ランダム化比較試験とは？例を使って無作為化のメリットデメリットをわかりやすく解説

医薬研究において、”比較する”というのは、非常に重要な観点です。

比較することによって初めて、目的とする治療の効果などに結論をつけることができます。

そして、”この比較結果は本当に意味のあるものである”というのを担保してくれるのが、ランダム化です。

そして、ランダム化を行なったランダム化比較試験（Randomized Controlled Trial：RCT）は、得られる結果のエビデンスがとても高いことで知られています。

この記事では、ランダム化比較試験（Randomized Controlled Trial：RCT）に関してその目的と、問題点をわかりやすく整理します！

ランダム化比較試験（無作為化比較試験、RCT）とは？例を用いて解説

まずは、ランダム化比較試験（無作為化比較試験、RCT）という試験はどういうものかを整理しましょう。

ランダム化比較試験（無作為化比較試験、RCT）とは、比較したい群（例えば、新薬群とプラセボ群）に入るサンプルが、ランダムに決まっている試験のことを指します。

ランダム化比較試験（無作為化比較試験、RCT）の例

例えば、がんに対する新薬の効果を確かめる臨床試験に、がん患者であるAさんが参加したとします。

がん患者であるAさんは病気を治したいので、新薬群に入りたいと思っています。

しかしAさんの希望は無視して、Aさんが新薬群になるのか、それとも比較するプラセボ群に入るのかを、ランダムに決めてしまうということです。

同様にして、Bさんが入ってきたときも、新薬群になるのか、それともプラセボ群になるのかを、ランダムに決めます。

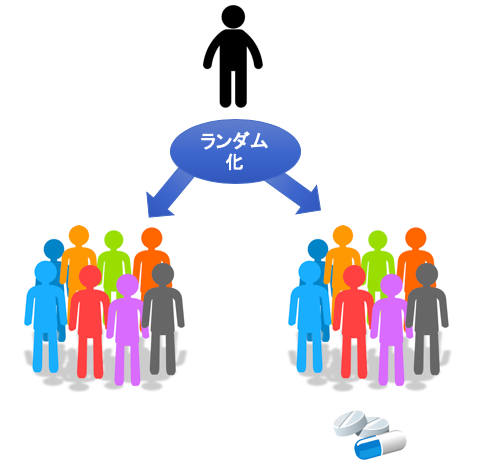
このように、試験に参加した患者さんがどちらの治療を受けるかをランダムに決めて比較する試験を、ランダム化比較試験（無作為化比較試験）と呼びます。

ランダム化比較試験の目的やメリットは？

では、なぜランダム化をする必要があるのでしょうか。

その目的を確認しましょう。

なにかを明らかにしたいとき、基本的には比較をする必要があります。

このとき、明らかにしたいこと以外の因子、たとえば性別や年齢などの背景因子を、群間で揃えるということが必要になります。

なぜなら、背景因子が揃っていないことには、得られた結果が治療の効果によるものなのか、それとも背景因子の偏りによって生じたものなのかが、区別できなくなってしまうからです。

いわゆる、交絡バイアスがもたらした結果なのか、ということの区別が付かなくなってしまうのです。

では、群間でそれらの背景因子を揃えるために、アイデアとしてはなにができるでしょうか？

ランダム化以外に群間の背景因子を揃えるアイデア：マッチングするという考え方

背景因子を揃えるため1つの策としてはマッチングです。

最近では、傾向スコアマッチング（プロペンシティスコアマッチング）なども有名ですよね。

たとえば、群間で性別を揃えるとします。

男性2人が揃ったときに、どちらか一方を新薬群、一方ではプラセボ群に割り当てます。

これを他の男性2人に対しても新薬群とプラセボ群に、女性2人に対しても新薬群とプラセボ群というように順次割り振っていけば、必ず群間で性別は揃うことになります。

ただし，マッチングをするときに1つだけ厄介なことがあります。

それは“マッチングしようとしている背景情報（この例では性別）のみしか揃わない”ということです。

つまり，性別は揃うが，年齢や体重や血圧などは揃わない可能性があります。

この場合，どうしたらよいでしょうか？

すべての因子をマッチングさせればいいでしょうか？

しかしすべてをマッチングさせようとすると、膨大な期間や費用がかかることになり、現実的ではありません。

そう、マッチングには限界があるのです。

ランダム化が背景因子を揃える唯一の方法

マッチングでは、膨大な背景因子に対して対応できない点が問題点でした。

そのため、群間で背景情報を揃える唯一の方法としてランダム化が重要になるのです。

ランダム化の恩恵は，さまざまな背景情報が“平均的に”等しくなるということ。

一つひとつの因子では群間に有利/不利が出てくる可能性はあります。

しかし、既知なのか未知なのかにかかわらず、すべての因子トータルで考えた場合に、群間の有利/不利が平均的に揃うということです。

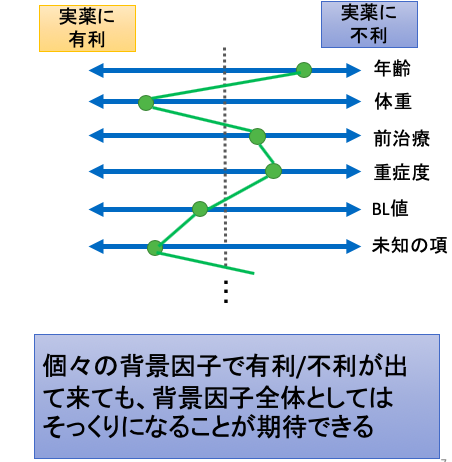
「既知なのか未知なのかにかかわらず」という点が、ランダム化の非常に重要な部分になります。

多変量解析や傾向スコアを使った解析などで、データを取得している背景因子を考慮することはできるのですが、未知の交絡因子（データがとられていない交絡因子）がある場合には、どうしても解析的に考慮することが不可能です。

そのため、未知の交絡因子（データが取られていない交絡因子）についてもバランスを考慮できることは、ランダム化にしかできないことになります。

ランダム化比較試験の問題点やデメリットは？

かなりメリットが大きく感じられるランダム化。

では、ランダム化の問題点はあるのでしょうか？

完全なランダム化（完全無作為化）の場合の問題点やデメリット

完全なランダム化の場合には、いくつか問題点が挙げられます。

1. 群間で症例数が揃わない可能性がある
2. 平均的には群間で有利/不利はないが、結果に対して重要な影響を与える背景因子が揃わない場合がある

完全にランダムにすると、当然ながら群間で症例数が揃わないこともあります。

各群で100例ずつ入れたい試験だったのに、80例と120例になってしまうことも。

また、完全なランダム化では背景因子が平均的に群間で揃いますが、もし結果に対して重要な影響を与える背景因子があった場合、その因子が群間で偏る場合があります。

その時には、交絡バイアスが生じてしまいますね。

なので、これらの問題点をどうにか解消する必要があります。

ランダム化の問題を解決する：動的割付

まずは、群間で症例数が揃わないことに対する問題の解決策です。

この問題に対しては”動的割付”という方法がとられることが多いです。

完全なランダム化の場合、Aさんが参加するときも、続いてBさんが参加するときも、新薬群かプラセボ群かに割付られる確率は1/2です。

しかし動的割付を採用すると、最初の参加者であるAさんは、新薬群かプラセボ群かに完全なランダム化で割付られます。

ここまでは完全ランダム化と同じです

動的割付では、Bさんが入る時に、完全なランダム化じゃなくするのです。

Aさんがもし新薬群に割付られているのであれば、Bさんはプラセボに入る確率を70%にして新薬群に入る確率を30%にします。

（70%や30%は例です。50%ではない、ということが重要です。）

で、Bさんがプラセボ群に入ったとしたら、新薬群はAさん1例、プラセボ群はCさん1例で揃っています。

揃っている場合、次のCさんはどちらの群になるかは完全なランダム化で決まります。

つまり、それまでに入っている各群の症例数が揃っているかどうかで、次に入る症例のランダム確率を変えてしまう、というのが動的割付です。

ランダム確率が動くため、動的、という言葉が使われています。

この動的割付は群間の症例数を揃えるのにすごく良い方法なのですが、最近ではあまり行われなくなってきました。

というのも、割付確率を70%にするということを「ランダムと言っていいのか？」という疑問があるためです。

そのため、動的割付を採用する場合には、動的割付じゃないとダメな理由をプロトコルに記載しておく必要があります。

ランダム化の問題を解決する：層別割付

完全なランダム化では背景因子が平均的に群間で揃いますが、もし結果に対して重要な影響を与える背景因子があった場合、その因子が群間で偏る場合があります。

この問題を解決するのが、層別割付（層別ランダム化）という方法です。

例えば、結果に重要な影響を与える因子が性別だったとします。

その時、男性という層と、女性という層ごとにランダム化をするのが、層別ランダム化です。

この方法を採用することによって、新薬群とプラセボ群で、男女の割合が同じになることが期待できます。

用語の整理として、層別ランダム化をする際に考慮したい背景因子のことを、層別因子と呼ぶことがあります。

ランダム化比較試験によって防ぐことができるバイアスは？

このランダム化によって防ぐことができるバイアスは、交絡バイアスです。

交絡バイアスを防ぐことができるということは、群間での比較結果が信用できるということになります。

交絡因子の調整は、共分散分析で行うことができますが、あくまでバイアスは事前に防ぐものです。

そのため、ランダム化をできる状況にあるのであれば、ランダム化をした方が結果の信用性は明らかに高くなります。

ランダム化をしていれば、被験者背景の検定は不要

このランダム化を理解できると、被験者背景の検定は不要であることがわかります。

この図の通りですね。

一つ一つの背景情報を見れば、差が出てくる背景因子も出てきます。

しかし、ランダム化の恩恵は”群全体で似通った集団を作ることができる”ということなので、一つ一つの背景情報に着目する必要はないのです。

それに、統計学検定では「同じ」ということを示すことはできません。

有意差がなかった時に「群間で違いがない」としている発表をみたことがありますが、有意差がない＝同じ、ということは言えないので注意してください。

逆にいえば、ランダム化を実施していない時には、積極的に被験者背景がどんな状況になっているのかを確認する必要があります。

繰り返しになりますが、ランダム化をしていなければ集団として似ているかどうかを保証できないため、得られた結果が治療効果の差なのか、それとも被験者背景の違いによるものなのかを区別できなくなってしまうためです。

ランダム化比較試験（無作為化比較試験）まとめ

ランダム化とは、参加者が新薬群かプラセボ群かどちらの治療を受けるのかを、ランダムに決めてしまう方法です。

これによって交絡バイアスを防ぐことができ、比較結果の信用性が高まります。

そして完全なランダム化ではいくつか問題点が出てきますので、その場合には動的割付や層別ランダム化などの方法を検討する必要があります。