統計学における正規性の検定は、データが正規分布に従うかどうかを確認するための手段の一つです。
正規分布とは、平均値を中心に左右対称のベルカーブを描く分布で、多くの自然現象や社会現象がこの分布に従っています。
正規性の検定は、特にパラメトリック統計手法を適用する前に確認するための手段というイメージがあり、データが正規分布に従っているかを検定によって確認することで、分析の妥当性を保証しようとします。
しかし、この検定が常に必要か、という疑問があるのです。
検定はサンプルサイズの大小でP値に影響があるため、実際のデータ分析では、正規性の検定を行う代わりに、ヒストグラムやQQプロットなどの視覚的な方法でデータの分布を評価し、分析の適切性を判断するアプローチが推奨されることもあります。
この記事では、まず「正規性の検定」とは何かを解説し、その後、なぜ多くの場合、正規性の検定を行わずにヒストグラムやQQプロットによる評価が推奨されるのかについて、その理由と実際のデータ分析での適用例を交えて説明していきます。
Contents
「正規性の検定」とは何か？
正規性の検定は、統計学においてデータセットが正規分布（ガウス分布）に従っているかどうかを調べる手法。
正規分布は、自然界や人間の行動、測定誤差など、多岐にわたる現象において観察されることが多いため、多くの統計的手法や理論がこの分布を前提としています。
正規性の検定には何がある？
正規性の検定にはいくつかの方法があります。
- シャピロ・ウィルク検定
- コルモゴロフ・スミルノフ検定
- アンダーソン・ダーリング検定
などがあります。
これらの検定は、得られているデータセットが正規分布に従っているかどうかを統計的に評価し、結果としてp値を提供します。
p値がある閾値（通常は有意水準0.05）未満の場合、データセットが正規分布から逸脱していると判断されます。
正規性の検定の問題点
しかし、これらの正規性検定はサンプルサイズに影響されるため、完全に正規分布なのかどうかを判定しているかは疑わしいです。
また、実際のデータ分析の文脈では、データが完全に正規分布をしている必要はないことが多いです。
統計学の中心極限定理は、サンプルサイズが大きければ、推定値の分布は正規分布に近づくことを示しています。
そのため実際のデータ分析においては、サンプルサイズが十分に大きければ、多少の分布の歪みがあっても、多くの統計的手法が有効に機能することを意味しています。
サンプルサイズが小さいと検定結果が不安定である
正規性の検定をはじめとする統計学的検定は、特にサンプルサイズが小さい場合に不安定になります。
つまり、小さなデータセットでは、たとえわずかな偏りや外れ値が存在しても、検定結果が大きく影響を受ける可能性があるのです。
正規性の検定は不要？
ここまでの話を総合すると、正規性の検定は便利な側面がある一方で、必ずしもデータの分布を正確に表現するような検定ではないこともわかります。
私自身は、正規性の検定は不要だと思っている立場です。
理由は、検定である以上はサンプルサイズの影響があるため。
特にサンプルサイズが小さい場合に検定結果は不安定であり、結果的にデータを誤って正規もしくは非正規と判断することがあります。
逆に、サンプルサイズが非常に大きい場合は、実際には無視できる小さなばらつきであっても、検定により正規分布ではないと判断されることがあります。
サンプルサイズにより検定結果が左右されることを考えた場合に、正規性の検定は不要だと思うのです。
正規性の検定をしなければ、何で正規分布かを判断するの？
正規分布かどうかを判断するために私がお勧めするのは、正規性の検定を行う代わりに、ヒストグラムやQQプロットなどの視覚的ツールを使用してデータの分布を評価することです。
これらの方法は、データがどのように分布しているかを直感的に理解するのに役立ちます。
正規分布の判断に有用なヒストグラムとは？
ヒストグラムは、連続データを一定の区間に分け、各区間に含まれるデータ点の数を棒グラフで表したもの。
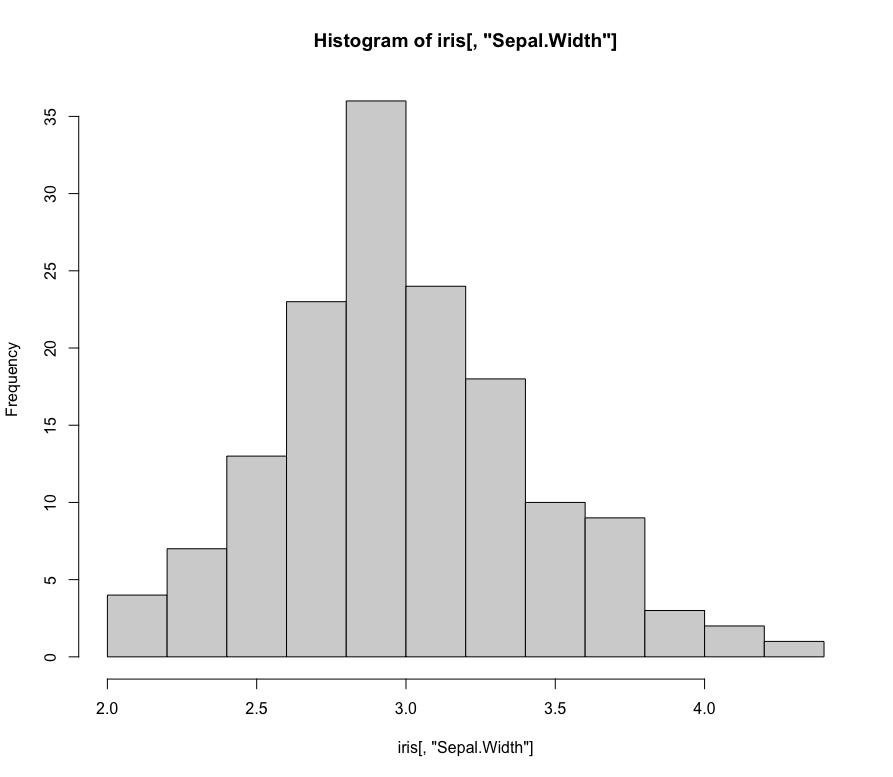
データの分布形状を視覚的に捉えることができるため、正規性の評価に役立ちます。
データが正規分布に従っている場合、ヒストグラムはベル形の曲線を描きます。
歪みや尖度などの特性も視覚的に評価することができます
＞＞RStudioで箱ひげ図やヒストグラム・散布図を綺麗に出力する方法
正規分布の判断に有用なQQプロットとは？
QQ（Quantile-Quantile）プロットは、サンプルデータの分位数を理論上の分布（この場合は正規分布）の分位数と比較することで、二つの分布がどの程度似ているかを視覚的に評価するグラフです。
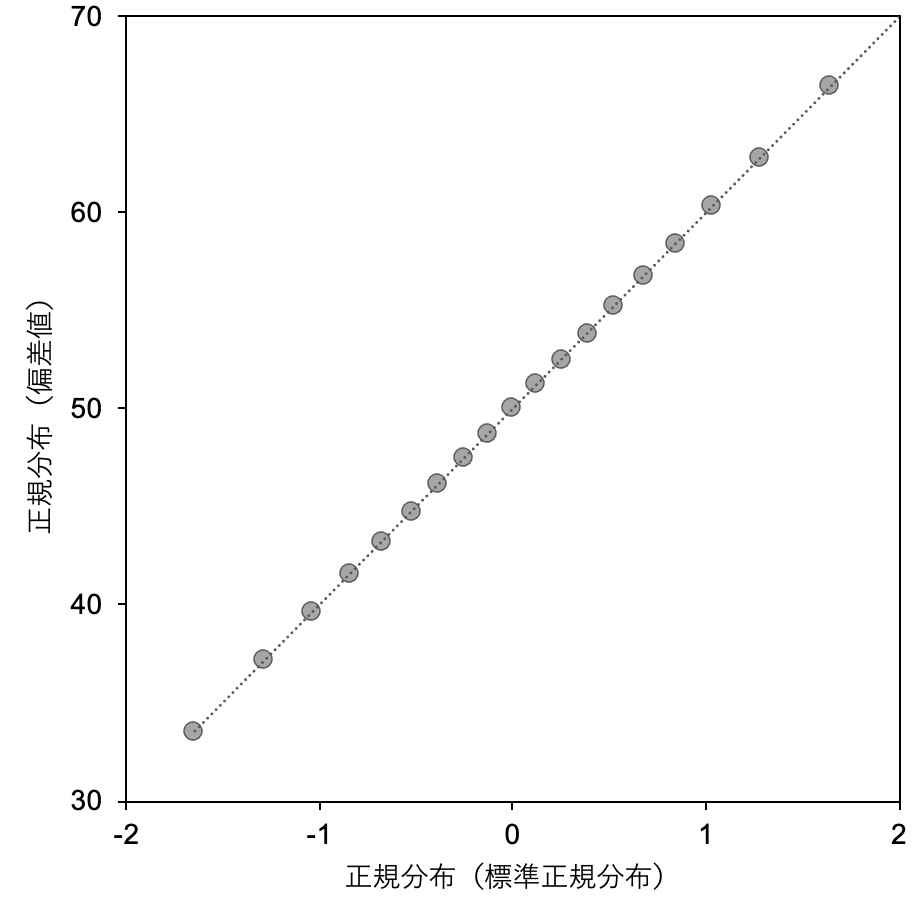
データが正規分布に従っている場合、QQプロット上の点は一直線に並びます。
直線からの逸脱は、データが正規分布から外れていることを示唆します。
QQプロットは、データセット内の外れ値や異常なデータポイントを識別するのにも役立ちます。
プロット上で大きく逸脱する点は、外れ値である可能性が高いです。
＞＞qqプロットとは？正規分布をどのような見方で判定すればいいの？
視覚的な方法で正規性が疑わしい場合はどうする？
データの正規性が疑わしい場合、正規性を仮定しないノンパラメトリック手法や、データの再サンプリングに基づくブートストラップ法などが、そのような状況で有効な選択肢となり得ます。
ノンパラメトリック手法の概要と適用例
ノンパラメトリック手法は、データの分布に関する厳密な仮定を必要としません。
これらの手法は、データの順位や中央値などの記述統計に基づいており、データの分布形状に左右されにくいため、正規分布でないデータに対しても適用可能です。
- マン・ホイットニーU検定（ウィルコクソンの順位和検定）：対応のない2群の検定
- クラスカル・ウォリス検定：三つ以上の独立したサンプルの検定。分散分析（ANOVA）のノンパラメトリックな代替手法です。
これらのノンパラメトリック手法は、データの正規性に関わらず、様々な状況でデータの比較や分析を行うための強力なツールとなります。
ブートストラップ法とその適用
ブートストラップ法は、元のデータセットからランダムにサンプルを繰り返し抽出し（再サンプリング）、そのサンプルを用いて統計量（例えば、平均、中央値、分散）の分布を推定する方法。
この手法は、データの分布形状に依存せず、特にサンプルサイズが小さい場合や、理論的な分布が不明な場合に有効です。
ブートストラップ法は、信頼区間の推定や標準誤差の評価に特に有用であり、データが正規分布に従っていない場合や、複雑な統計モデルを評価する際にも利用されます。
ブートストラップにより、データの不確実性を定量化し、より信頼性の高い統計的推論を行うことが可能となります。
まとめ
正規性の検定は便利な一方で、サンプルサイズの影響で結果が左右されることから、使用をお勧めしません。
ヒストグラムやQQプロットなど、視覚的な情報をもとにして判断していきましょう。
この記事を通じて、正規性の検定に頼ることなく、データの特性を理解し、分析するための方法について理解を深めていただけたら幸いです！
第1章：臨床研究ではなぜ統計が必要なのか？計画することの重要性
第2章：研究目的をどれだけ明確にできるのかが重要
第3章：p値で結果が左右される時代は終わりました
第4章：多くの人が統計を苦手にする理由
第5章：統計を使えるようになるために今日から何をすれば良いか？
第6章：統計を学ぶために重要な環境
もしあなたがこれまでに、何とか統計をマスターしようと散々苦労し、何冊もの統計の本を読み、セミナーに参加してみたのに、それでも統計が苦手なら…
私からプレゼントする内容は、あなたがずっと待ちわびていたものです。
