正規分布とは？わかりやすく標準偏差との関係もガウス分布に関して解説

“正規分布（ガウス分布）”は統計学で検定やモデル、推定などいろいろな場面で利用します。

正規分布（ガウス分布）は統計を学ぶ上で必須の知識。

でも私も最初はそうだったのですが、”正規分布（ガウス分布）”といえばなんとなく、山の形をした分布だ、、くらいのイメージの人もおられると思います。

できれば正規分布（ガウス分布）をわかりやすく理解したいですよね。

ということでこの記事では、統計学で最も重要な確率分布である”正規分布（ガウス分布）”と、その性質についてわかりやすく説明していきます。

 

正規分布（ガウス分布）とは簡単にいうとどんな分布？なぜ重要なの？

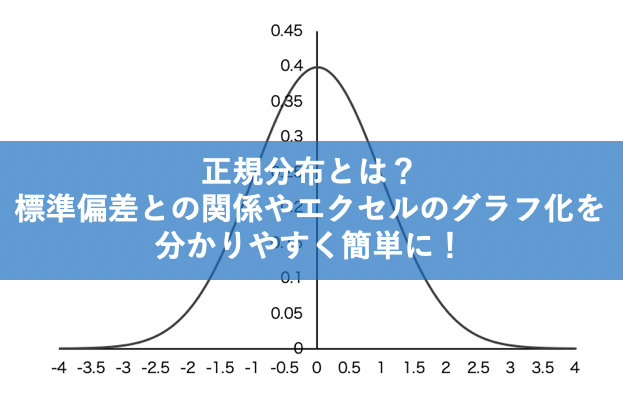
正規分布（又の名を”ガウス分布” ）は、下の図のような形をしています。

この形が鐘の形に似ているため、正規分布が描く曲線のことをベルカーブとも呼びます。

下図の横軸は観測データ(確率変数)を、縦軸はその値が生じる確率(確率密度)を表しています。

正規分布の特徴を挙げると、以下の点を挙げることができます。

• 左右対称である
• 平均の観測データが生じる確率が最も大きい
• 平均から離れるほど生じる確率は小さくなる

 

ではなぜ、統計学を学ぶ上で正規分布が重要となるのでしょうか?

理由は、自然現象や社会現象には、正規分布に従うものが多くあるからです！

どういうことかというと、“母集団の分布にかかわらず、母集団から抽出された標本の数が十分に多い場合、標本平均の分布は正規分布に従う”といった性質が存在するからです。

この性質のことを、中心極限定理、と呼びます。

この性質が存在するため、数多くの統計手法では、データが正規分布に従うと仮定が用いられます。

 

正規分布（ガウス分布）の性質を簡単にわかりやすく

正規分布の性質として重要なことは2つです。

1. 正規分布の形は平均と標準偏差(データのバラツキ)で決まる。
2. 標準偏差がわかれば、その範囲にどれくらいの観測データが含まれているかが分かる

 

正規分布（ガウス分布）の重要な性質1：グラフの形は平均と標準偏差で決まる

正規分布の形は平均と標準偏差（データのバラツキ）で決まります。

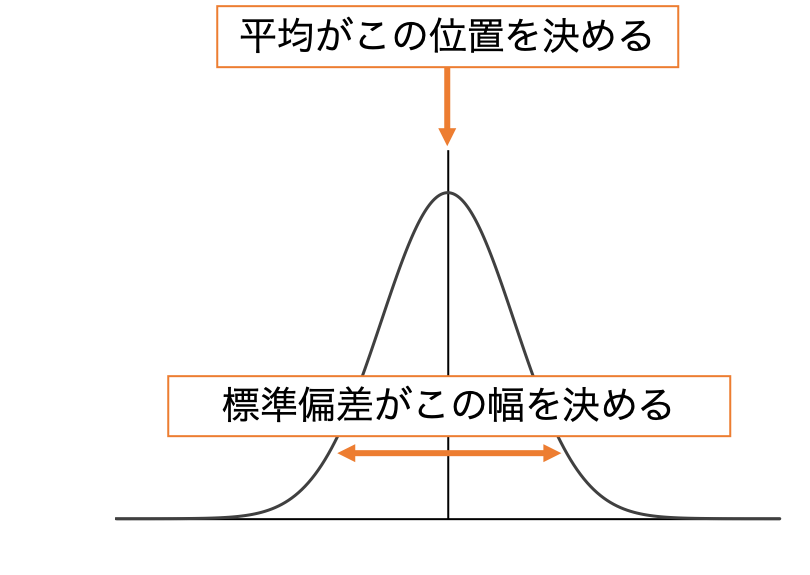
平均値は正規分布の中心の位置を決定します。

標準偏差は正規分布の左右の広がり度合いを決定します。

正規分布を式で表すと、下の式になります。

少しややこしいですね。（式自体は覚えなくていいですよ！）

 

この標準偏差という語句は、正規分布とセットで出てくる超重要単語。

それは、正規分布の２つ目の性質を説明する上で、標準偏差が必要だからです。

 

正規分布（ガウス分布）の重要な性質2：標準偏差がわかれば、その範囲にどれくらいの観測データが含まれいるかが分かる

正規分布には、平均や標準偏差の値とは関係なく、次の性質があります。

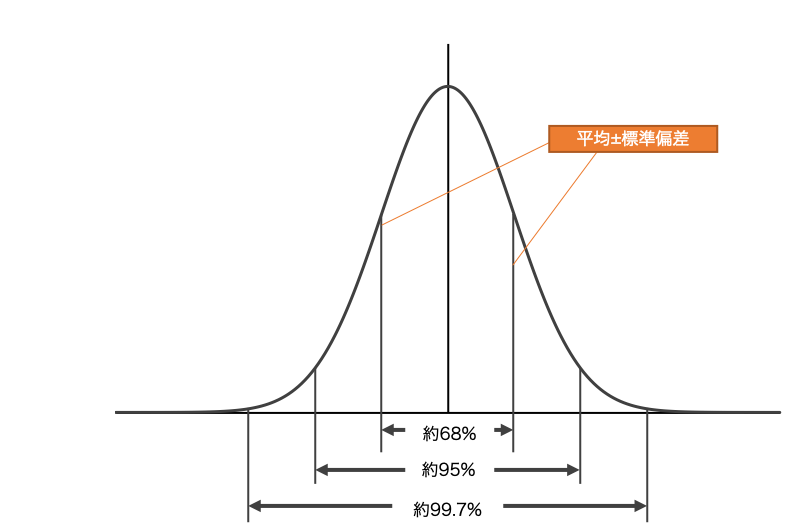
• 平均±標準偏差の範囲中に全体の約68パーセントのデータが含まれる。
• 平均±2×標準偏差の範囲中に全体の約95パーセントのデータが含まれる。
• 平均±3×標準偏差の範囲中に全体の約99.7パーセントのデータが含まれる。

 

つまり、標準偏差がわかれば、その範囲にどれくらいの観測データが含まれているかが分かります。

この2つ目の性質は、平均や標準偏差の値に関係ありません。

 

この性質を用いたもっと有名なものは、成績を表す偏差値です。

＞＞偏差値とは？平均値と標準偏差との関係！

他にもこの性質は品質管理などの様々な分野に利用されています。

 

正規分布（ガウス分布）をエクセルで描く

1つ目の性質は式だけでは、イメージするのは難しいと思います。

そこで、イメージを深めるために、Excelで正規分布を描いてみましょう。

より詳細にエクセルで正規分布の書き方を知りたい方は、下記の記事からどうぞ！

＞＞エクセルで正規分布をグラフ化する！

 

Excelで正規分布を書くには、NORM.DIST関数を使う

Excelで正規分布を書くためには、NORM.DIST関数を利用します。

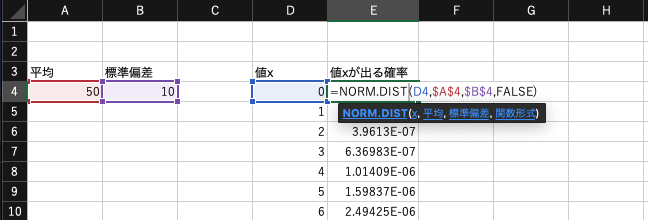
NORM.DIST関数では、値x、平均、標準偏差と関数形式のパラメータを用います。

今回はNORM.DIST関数の関数形式はFalseを選んでください。

このパラメータを入れるとNORM.DIST関数は、値xが出る確率を出力します。

 

今回は、平均が50で、標準偏差は10でやってみます。

まず、値xごとの確率を求めます。

次に。データ部分を選択し、挿入から散布図を選ぶと、

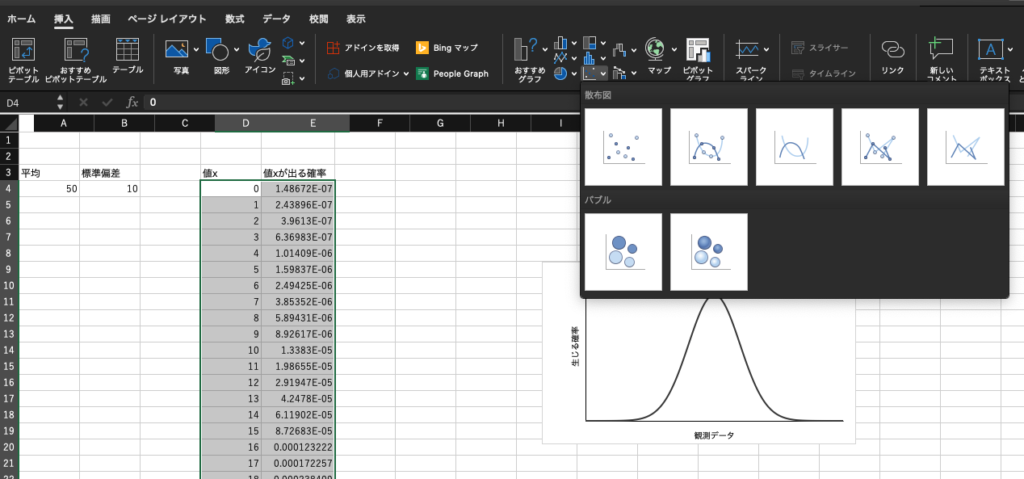
平均50で、標準偏差10の正規分布を描くことができました!

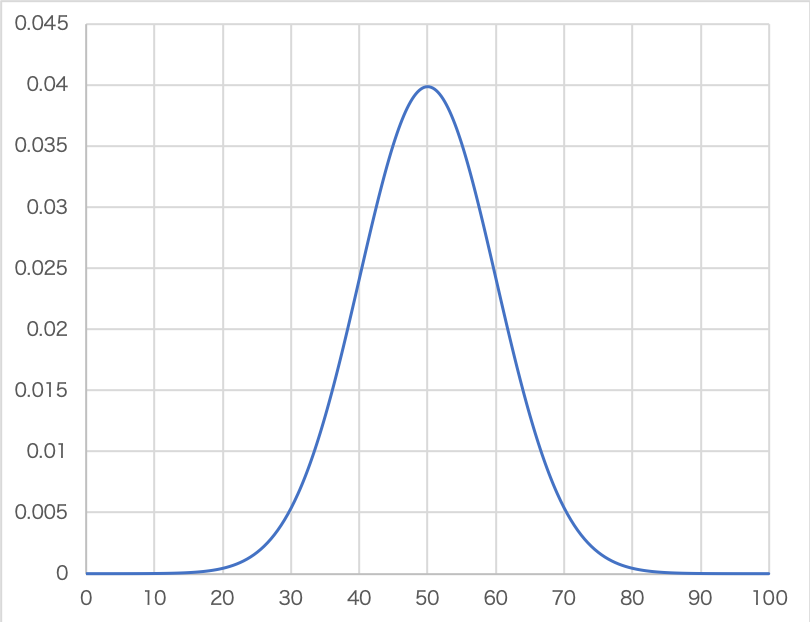
• 左右対称である
• 平均の観測データが生じる確率が最も大きい
• 平均から離れるほど生じる確率は小さくなる

上の性質のように、分布は左右対称です。

また、平均50が出る確率が最大となり、平均から離れると確率が小さくなることがわかります。

次に、平均と分散が変化すれば分布の形がどのように変化するかみていきましょう。

 

平均は正規分布の中心の位置を決める

平均は正規分布の中心の位置を決定します。

このことを確認するために、平均を変化させてみます。

先ほど使った、NORM.DIST関数の平均を変化させていきます。

その結果が下の図です。

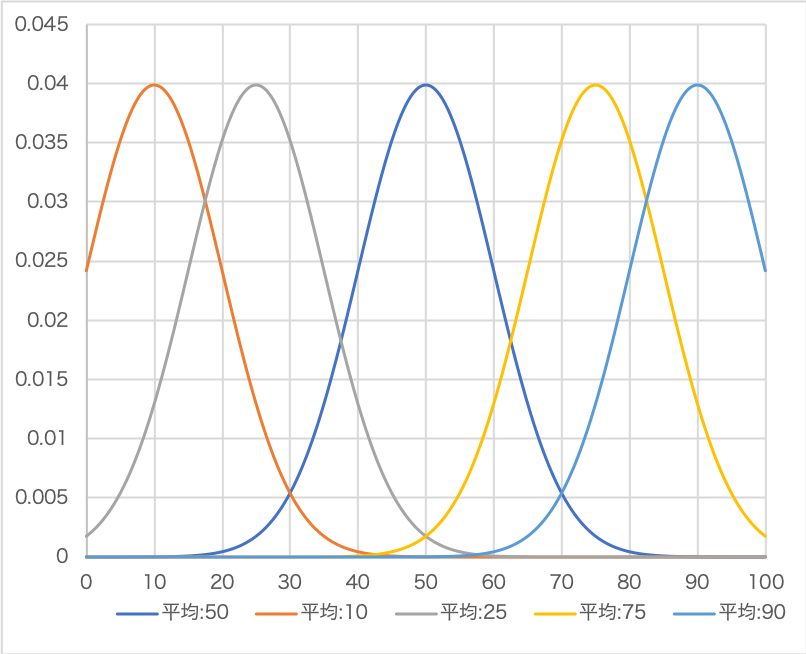
平均を大きくすると、正規分布は右に平行移動します。

平均を小さくすると、今度は正規分布平行は左に移動します。

一方、標準偏差は変えていないので、正規分布の形は変化していません。

つまり、正規分布の形には平均は関係しないです。

次に、標準偏差を変化させてみます。

 

標準偏差は正規分布の左右の広がり度合いを決定する

標準偏差は正規分布の左右の広がり度合いを決定します。

このことを、NORM.DIST関数を使って確認していきます。

今度は、標準偏差の値を変化させていきます。

その結果が下の図です。

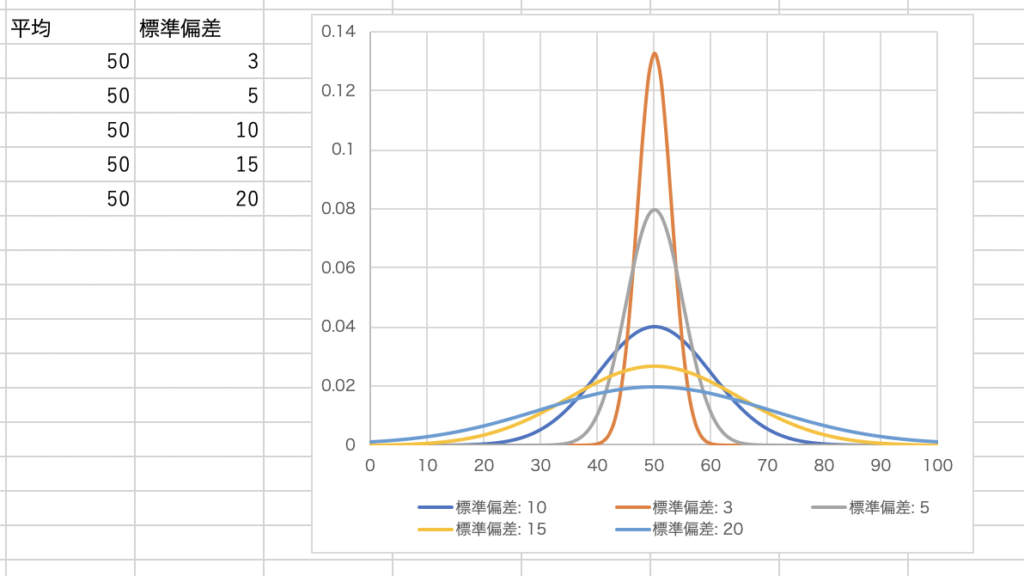
標準偏差が大きくなると、正規分布は左右の広がっていきます。

標準偏差が小さくなると、正規分布は上に鋭く尖った形になります。

一方で、正規分布の中心の位置は変化していませんね。

 

正規分布を標準化したもの：標準正規分布

平均と分散によって、正規分布はいろいろな形をとることができます。

その中でも特に、平均が0で、分散が1のものを”標準正規分布”と呼びます。

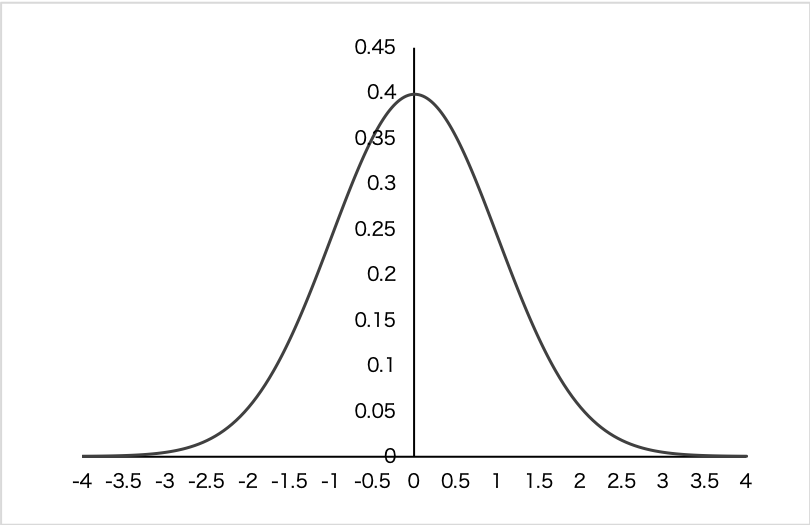
標準正規分布を用いるメリットは形が一つに決まっていることです。

標準正規分布が便利な理由はこちらの記事で解説していきます。

 

正規分布（ガウス分布）に関してまとめ

• 正規分布が重要なのは“母集団の分布にかかわらず、母集団から抽出された標本の数が十分に多い場合、標本平均の分布は正規分布に従う”という性質に由来する。
• 正規分布の形は、平均と標準偏差によって決まる。
• 標準偏差がわかれば、どの範囲にどれくらいの観測データが含まれているかが分かる
• Excelで正規分布を書くなら、NORM.DIST関数を用いる。
• 平均が0で、分散が1のものを標準正規分布と呼ぶ。

 

こちらの記事の内容を、動画で解説しています。

ぜひ記事内容と併せてご覧くださいませ。

理解が一層進むはずです。