qqプロットを聞いたことがありますか?
qqプロットは英語では、quantile-quantile plotといって、日本語に訳すなら分位-分位プロットと言います。
このqqプロットは二つの確率分布をプロットすることで比較する統計手法です。
色々な分布に適用できるのですが、実際には「得られているデータが正規分布に従っているかどうか」という観点の見方をするのに使われていますね。
今回はqqプロットについてわかりやすく説明していきます。
qqプロットとは?

qqプロットは英語のquantile-quantile plotの略称です。
quantileは日本語で「分位」という意味で、2つの確率分布を比較する手法です。
ここでの分位は、データがどの位置に分布しているかを相対的に見る数値のことで、データを昇順(小さい順)に並べて累積確率を求めることで決定します。
分位については
>>>>中央値(メジアン)は奇数と偶数で求め方が違う?エクセル関数などもわかりやすく
>>>>箱ひげ図とは?見方やエクセル作り方まで解説!外れ値や平均値も確認できる
これらのリンクでも説明しています。
qqプロットはこのように、分位を点にとって散布図として描写します。
グラフの見方など、詳しくは次の節で見ていきます。
qqプロットで何がわかるの?正規性の判断に用いられるグラフ

qqプロットでは、2つの比較したい分布が似ているか否かがわかります。
分かりやすく説明するために、実際に、いくつかの分布を比較してみてみます。
その前に要点を先に紹介すると、qqプロットでチェックするポイントは直線か直線ではないかです!
正規分布と正規分布のqqプロット
まずは二つの異なる正規分布を比較してみます。
正規分布についてはこちらで詳しく説明しています。
>>>>正規分布とは?簡単にわかりやすく標準偏差との関係もガウス分布に関して解説
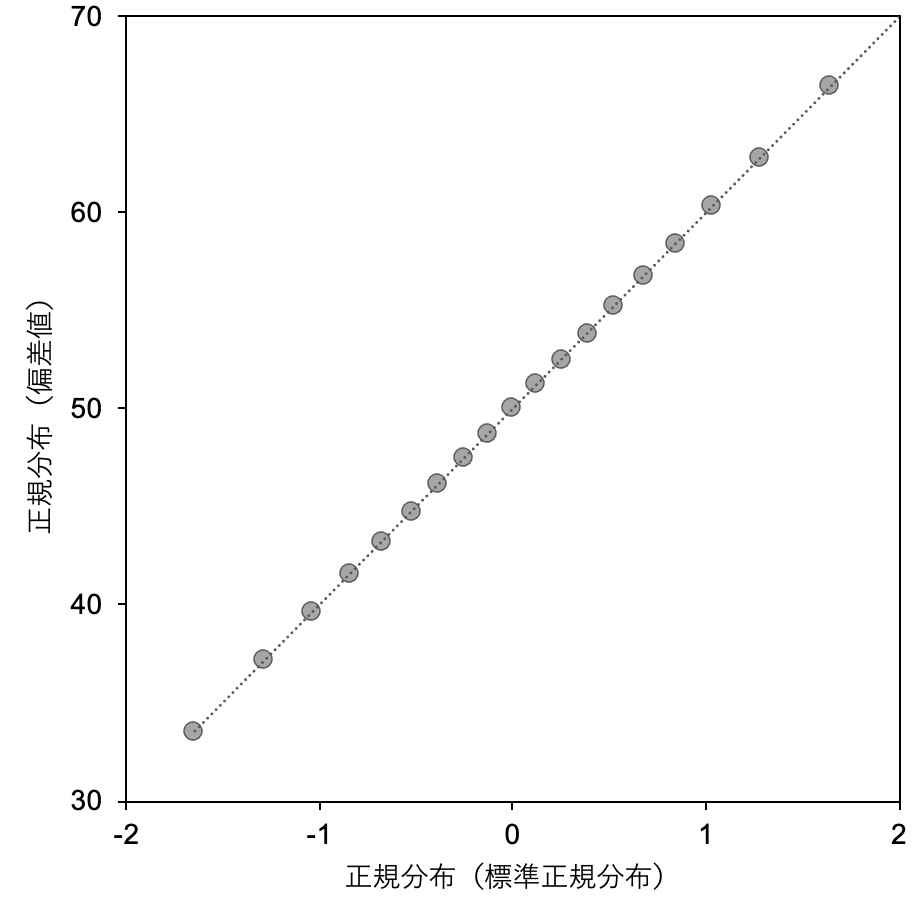
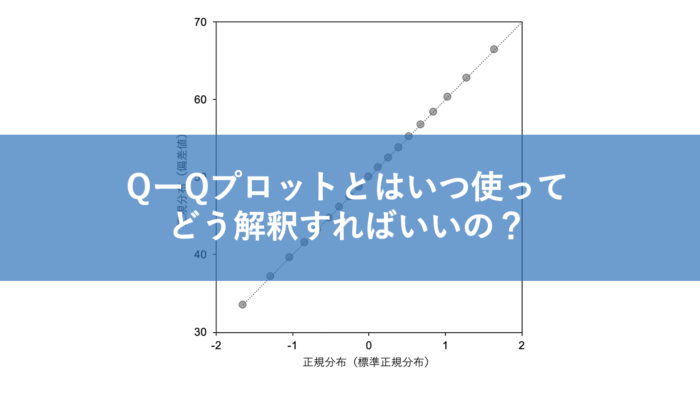
 ここでは、x軸に平均が0で標準偏差が1の標準正規分布と、
ここでは、x軸に平均が0で標準偏差が1の標準正規分布と、
y軸に平均が50で標準偏差が10の偏差値の二つを10分位で(累積頻度10%ごと)比較しています。
どちらも同じ正規分布なので、比較したプロットは直線の関係となっています。
qqプロットでは、分位数を用いるメリットとしては、分位数によってデータの分布のみを注目することで、実際のデータの値のスケールを考慮せずに比較できるというメリットがあります。
実際に上のプロットでも直線の関係ですが、x軸とy軸の値の範囲は結構ちがいます。
次に、違う分布の例として正規分布と対数正規分布を比較してみます。
正規分布と対数正規分布のqqプロット
正規分布と対数正規分布を比較プロットするとこのようになります。
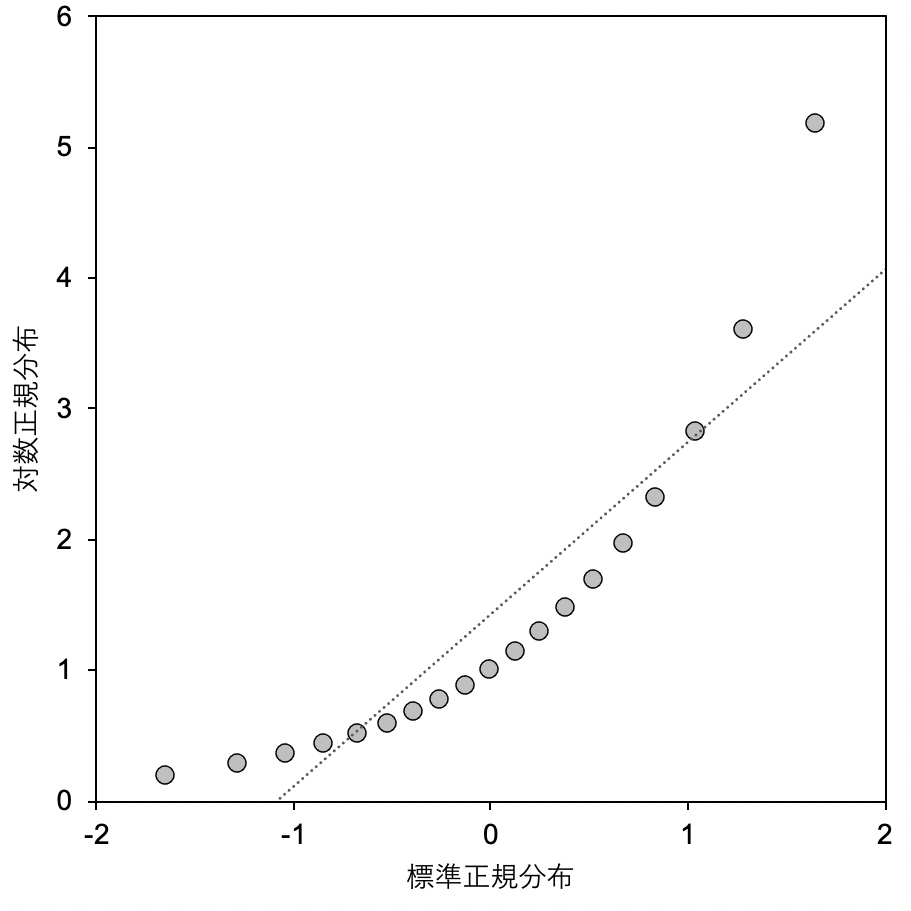
ここでは、x軸に平均が0で標準偏差が1の標準正規分布を、y軸には、平均が0で標準偏差が1の対数正規分布を10分位でプロットしています。
この二つは分布が異なるため、直線の関係にはなっていないですね。
qqプロットでは、二つの確率分布が異なるときはこのように直線ではない形になります。
この直線ではない具合を評価することで、データの値の分布についても調べるとができます。
最後に、二項分布と正規分布を用いて解説していきます。
正規分布と二項分布のqqプロット
正規分布と二項プロットを比較プロットするとこのようになります。
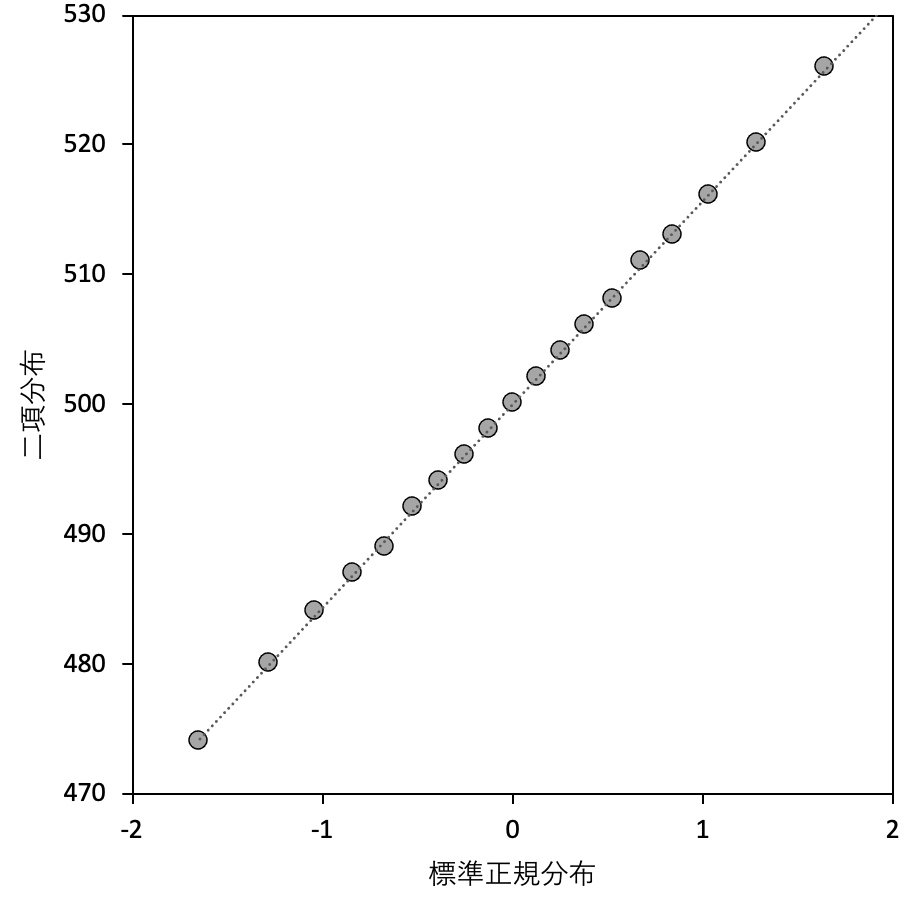
ここでは、x軸に平均が0で標準偏差が1の標準正規分布を、
y軸には、1/2であたりが出るコイン投げを1000回試行するときの二項分布を10分位でプロットしています。
二項分布についてはこちらで解説しています。
>>>>二項分布とは?わかりやすく正規分布との違いや近似できる問題も例を踏まえて
このqqプロットは直線の関係ですね。
二項分布と正規分布は異なる分布なのにどうして、直線の関係になるのでしょうか?
それは、二項分布は試行数nが大きくなると、近似的に正規分布になるというルールが存在するためです。
これは中心極限定理として知られている現象。
今回は1000回の試行を行っているため、正規分布に近似的に従うことになります。
このqqプロットでは、近似的に正規分布に従うという二項分布のルールを視覚化したことになります。
qqプロットはどういう時にときに使うの?見方はどうすればいい?
qqプロットは、あるデータの分布がある確率分布に従っているかを視覚的に調べるときに用います。
上の例でも見たように、
比較した二つの分布が同じ確率分布に従うとき、似ているときは、一直線に並びます。
比較した二つの分布が同じ確率分布に従わないときは、曲線になります。
これらの関係を実際のデータなどで調べることで、直感的に2つのデータの分布の形を調べることができます。
実際には「得られているデータが正規分布に従っているかどうか」という観点の見方をするのに使われていますね。
正規分布に従っているかどうかについて、正規性の検定を実施する方も多いかもしれませんが、検定はお勧めできません。
ヒストグラムやQQプロットで視覚的に確認する方がいいですね。
qqプロットをEZRで作成する方法!

では実際にEZRでQQプロットを作成してみましょう。
EZRでT検定を実施した時のLDHというデータを使って実施してみます。
EZRにQQプロットを作成する基となるデータを読み込む
ではここから、EZRにデータを取り込みます。
まずは、サンプルデータを適切な場所に保存しておきましょう。
EZRを開き、「ファイル」→「データのインポート」→「ファイルまたはクリップボード, URLからテキストデータを読み込む」を選択します。
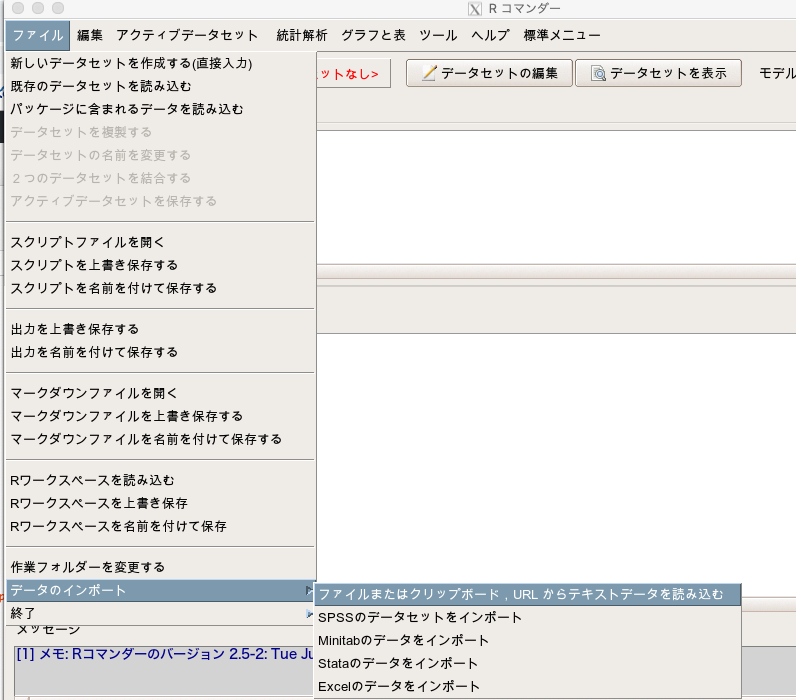
データセット名は「qqdata」にしましょう(実際はなんでもよい)。
そして「ローカルファイルシステム」と「カンマ」にチェックを入れてOKを押します。
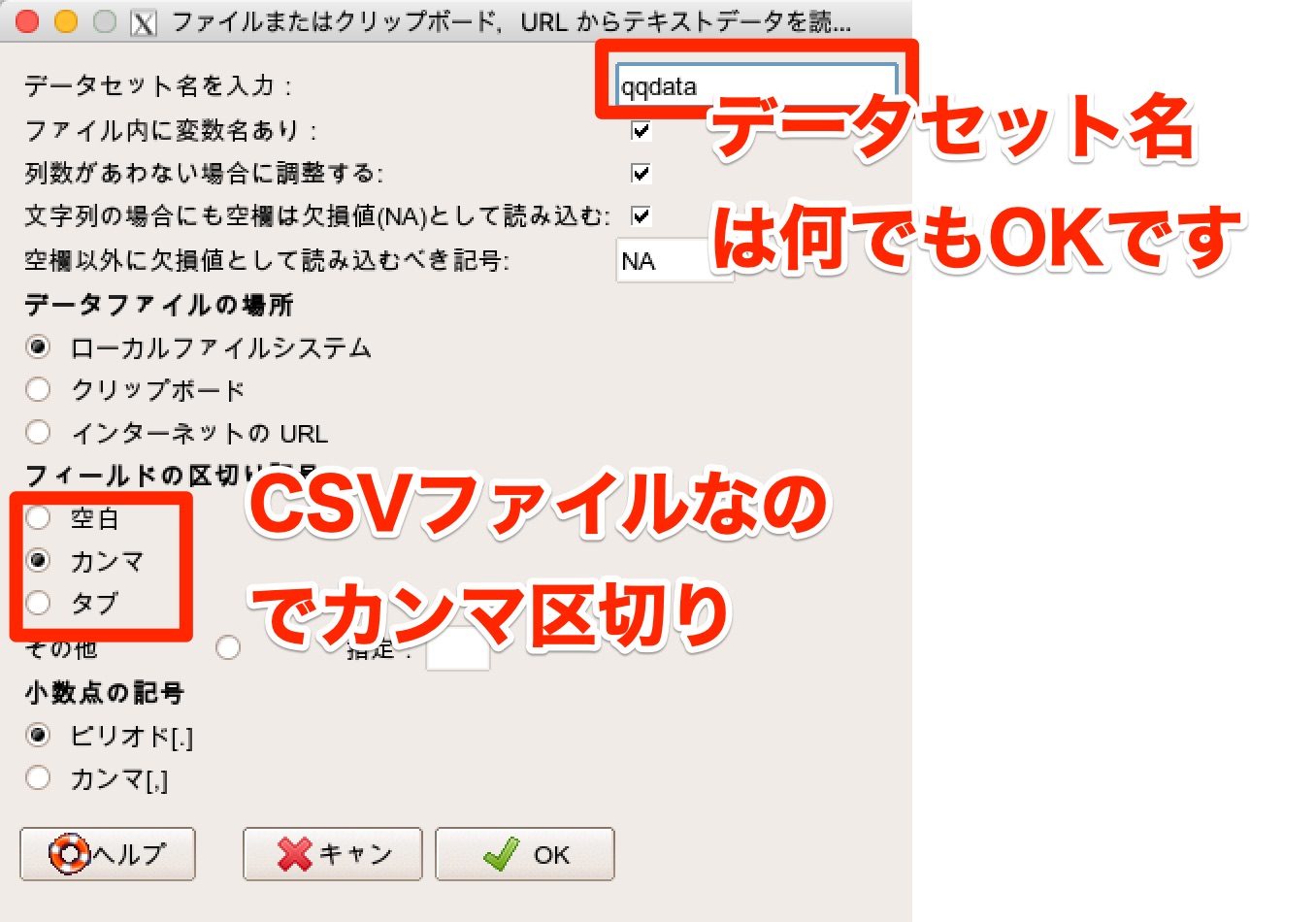
データセットが「qqdata」になっていることを確認し、「表示」を押してデータが正しく表示されれば取り込み完了です。

EZRでQQプロットを作成!
データが取り込まれましたので、早速QQプロットを作成しましょう!
「グラフと表」から「QQプロット」を選択します。
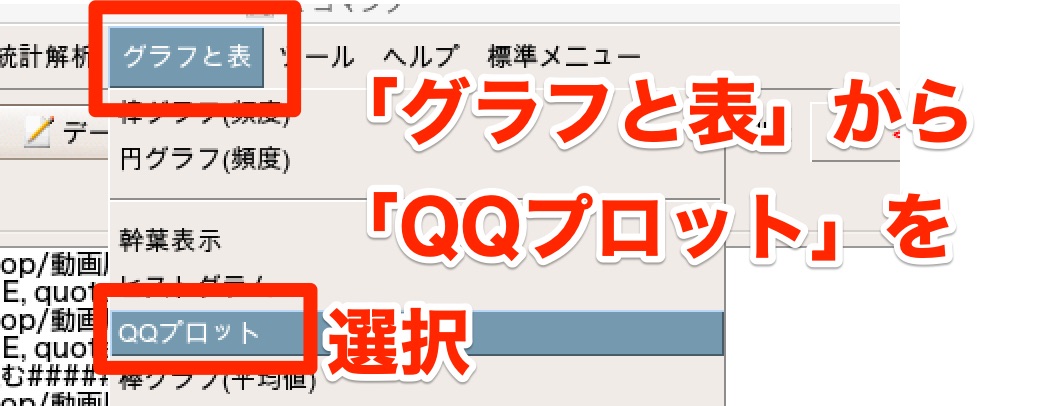
すると、どの変数をどんな分布かどうかを確認するか設定ができるようになります。
今回は「LDH」のデータを「正規分布」かどうか確認するので、以下のようなっ設定にします。
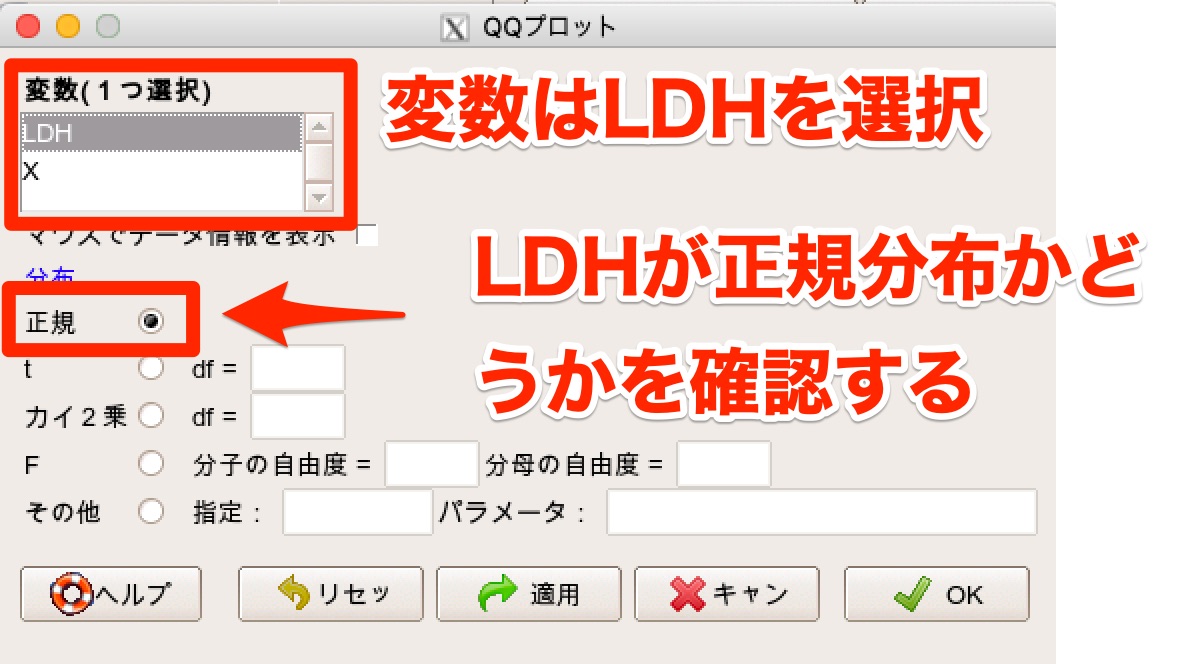
そして「OK」を押すと、以下のようなQQプロットが作成されます。
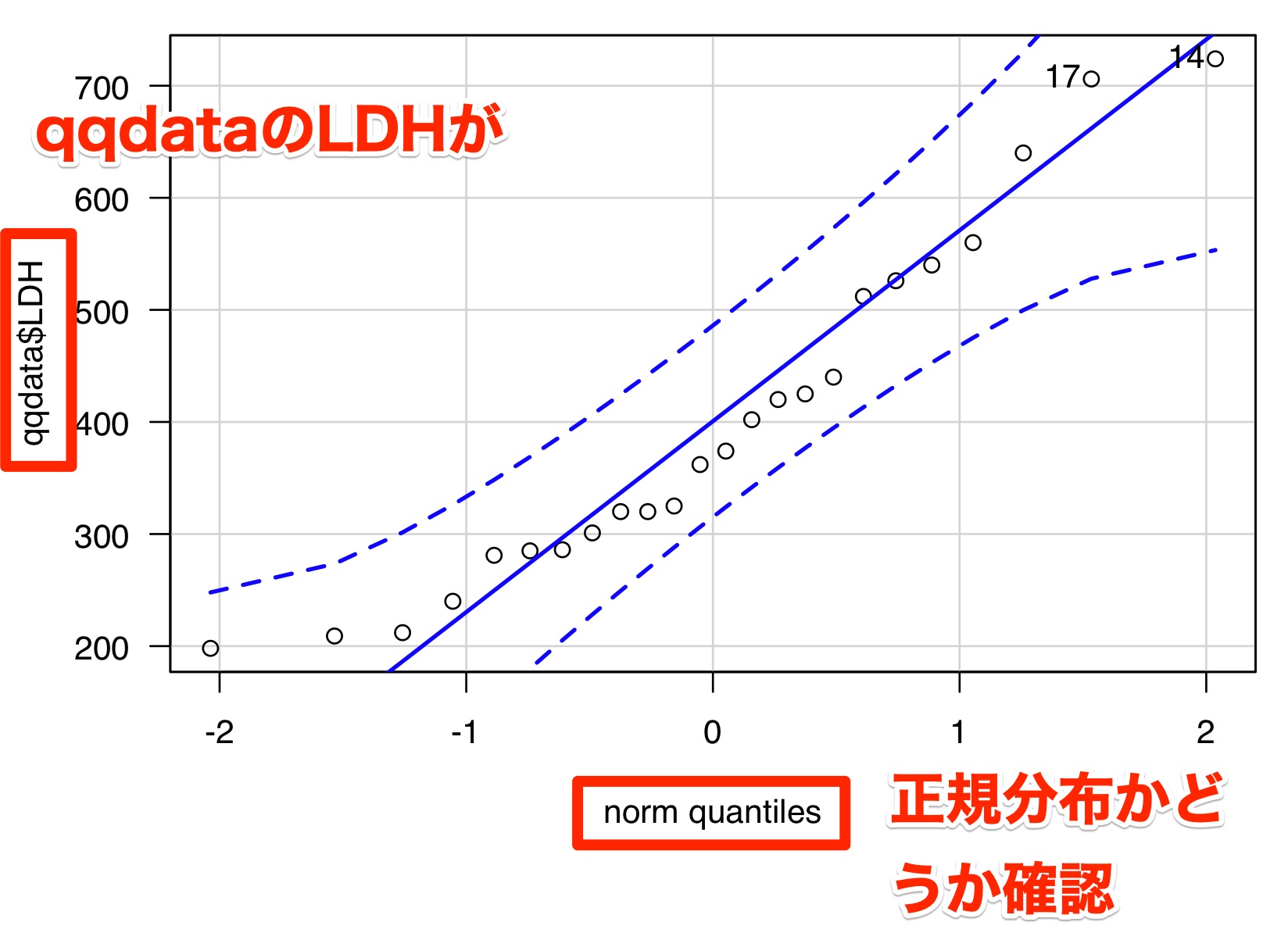
これで完了です!
結構簡単にQQプロットが作成できました。
QQプロットに関するまとめ

qqプロットは英語のquantile-quantile plotの略称です。
quantileは日本語で「分位」という意味で、2つの確率分布を比較する手法。
比較した二つの分布が同じ確率分布に従うときor似ているときは=点が一直線に並びます。
比較した二つの分布が同じ確率分布に従わないときは=点が直線にならない。
qqプロットでチェックするポイントは直線か直線ではないかです!













コメント
コメント一覧 (1件)
[…] 検定する各群すべてが正規分布に従うデータであること。(ヒストグラムやQQプロットなどの見た目判断でOK) […]