統計本の教科書の巻末には、必ずついている標準正規分布表。
数字がびっしり書かれていてとても難しそうだし、見方もわからない。。
でも、実は、標準正規分布表はとっても便利です!
ここでは、標準正規分布と標準正規分布表の見方、そしてZ値との関係について、わかりやすく説明していきます。
標準正規分布と標準化によるZ値の求め方は?

まずは標準正規分布について。
標準正規分布は、“ある範囲にどれくらいの観測データが含まれているか”を知るのにすごく便利です。
標準正規分布って何?
標準正規分布は、平均が0で、標準偏差が1の正規分布です。
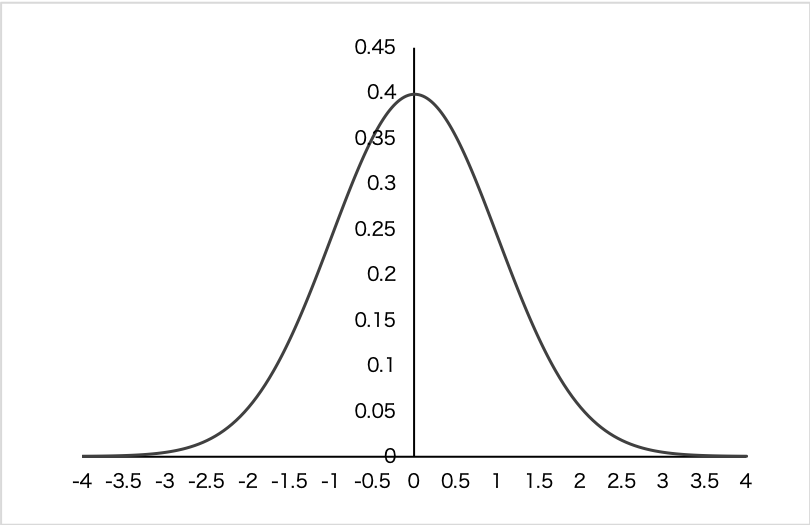
正規分布とは?簡単にわかりやすく標準偏差との関係やエクセルでのグラフ化を解説
で紹介しましたが、正規分布の2つの大事な特徴は
- 正規分布の形は平均と標準偏差(データのバラツキ)で決まる。
- 標準偏差がわかれば、その範囲にどれくらいの観測データが含まれているかが分かる
ことです。
標準正規分布では、平均も、標準偏差もすでに決まっている(平均は0、標準偏差は1)ため、1つの形しありません。
そのため、標準正規分布では2つ目の特徴”その範囲にどれくらいの観測データが含まれているかが分かる“にのみ注目することができます。
どのような形の正規分布でも、標準正規分布に変換することができます。
正規分布から標準正規分布に変換することを、”標準化”と呼びます。
- 標準正規分布とは、平均値が0で標準偏差が1の正規分布
- どんな正規分布でも”標準化”をすることで、標準正規分布に変換することができる
正規分布のデータを標準化(Z値への変換)してみよう
それでは、早速、標準化のやり方を紹介していきます。
標準化は次の2ステップで行います。
- データ値xから平均を引く
- データ値xから平均を引いた値を、標準偏差で割る
式で書くと下の式になります。
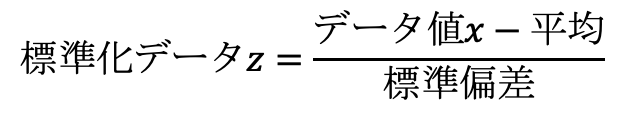
標準化したデータはz値(zスコア)と呼ばれます。
この簡単な操作だけで、どんな正規分布も標準化することができます。
次に標準化正規分布とセットで用いる、標準化正規分布表について紹介します。
標準正規分布表の見方や使い方!Z値がマイナスな時は?

標準正規分布表を使うと、正規分布に従うデータで、“あるz値以上(以下)が生じる確率が何%か”が一瞬でわかります。
標準正規分布表って何?
標準正規分表は”ある値以上が生じる確率”をまとめた表です。
“あるz値以上が生じる確率”は標準化分布でいうと、下図の緑色の部分の面積に対応します。
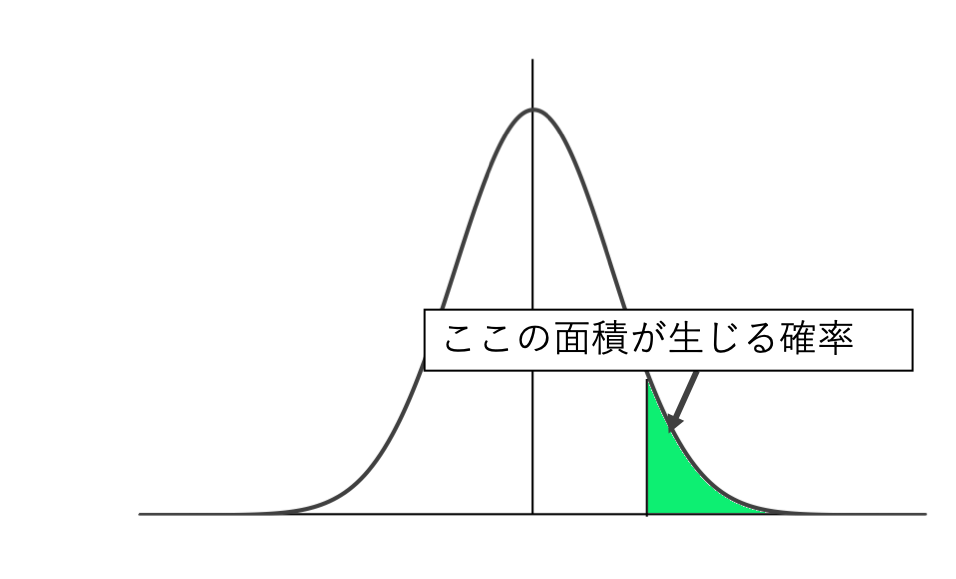
標準正規分布表には、様々なz値での確率(緑の面積)がまとめれています。
z値における、確率ではないので気をつけてください!!
標準化正規分布表の見方
標準正規分布表の見方は以下のようです。
- 一の位と小数点一桁目の数字を縦で探す。
- 小数点二桁目の数字を横で探す。
- 二つが交わるところの数値を読み取る。
標準正規分表には下のように数字がびっしり書かれています。
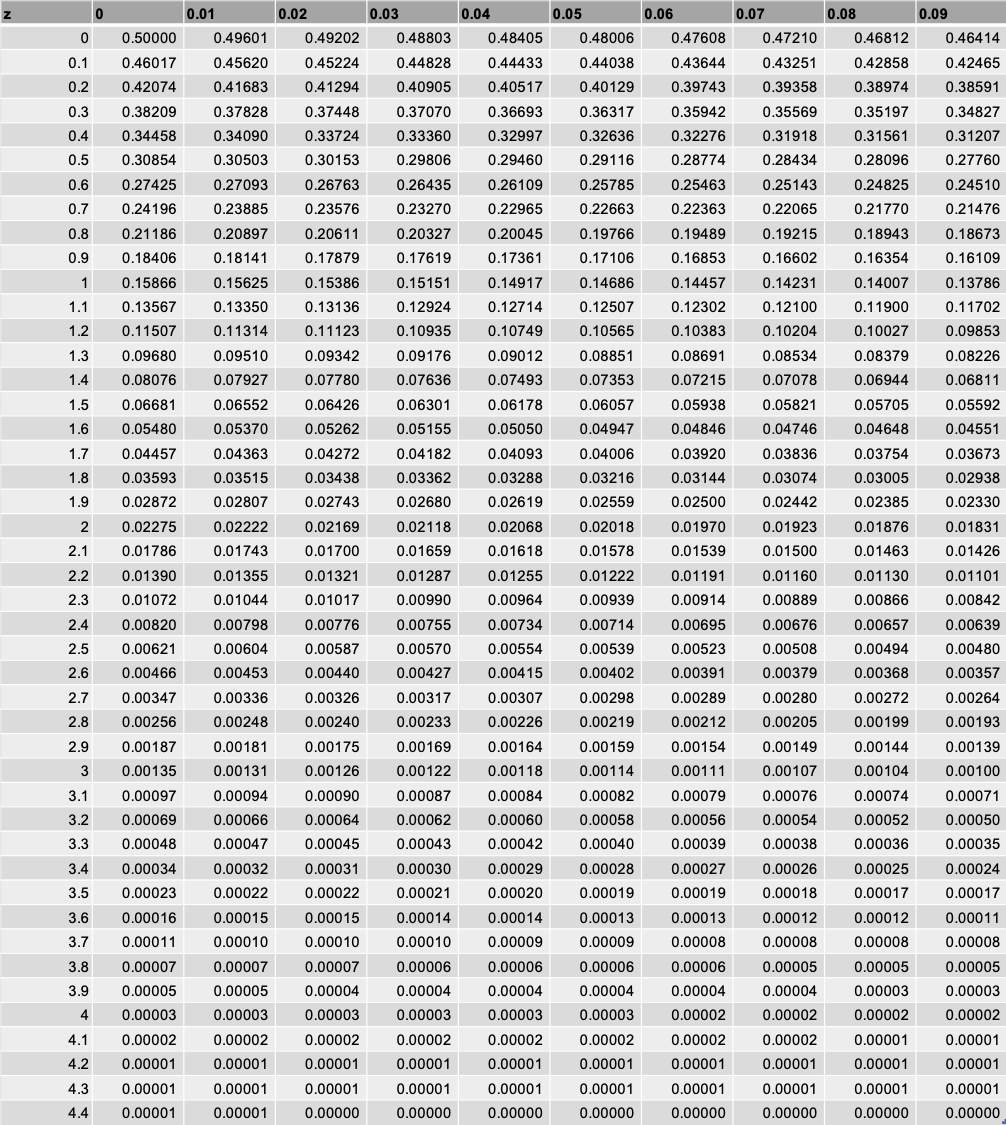
でも、見方は簡単です!!
例えば、z値が1.53を考えてみます。
はじめに、”一の位と小数点一桁目の数字を縦で探す”を行います。
z値が1.53では一の位と小数点一桁目は1.5です。
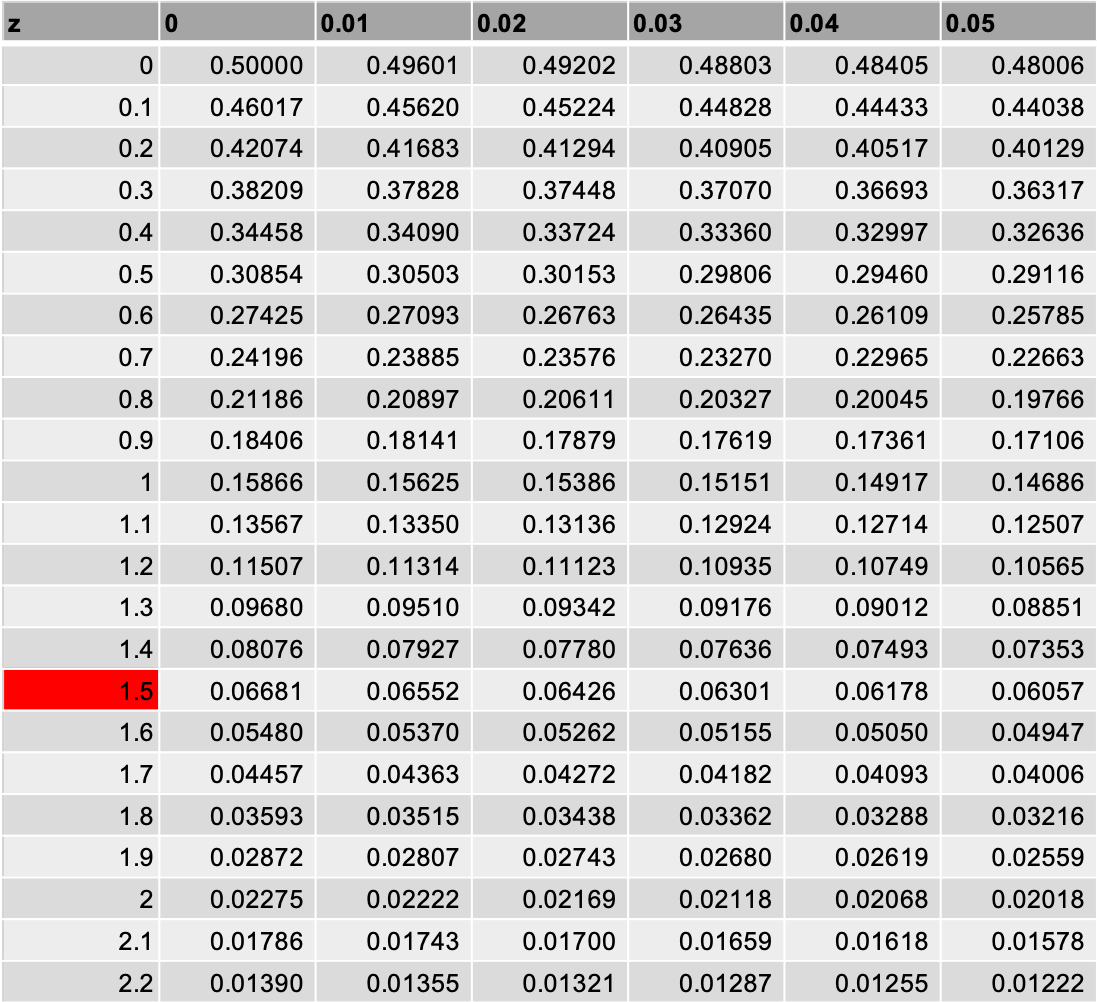
ありました。
次に、”小数点二桁目の数字を横で探す”を行います。
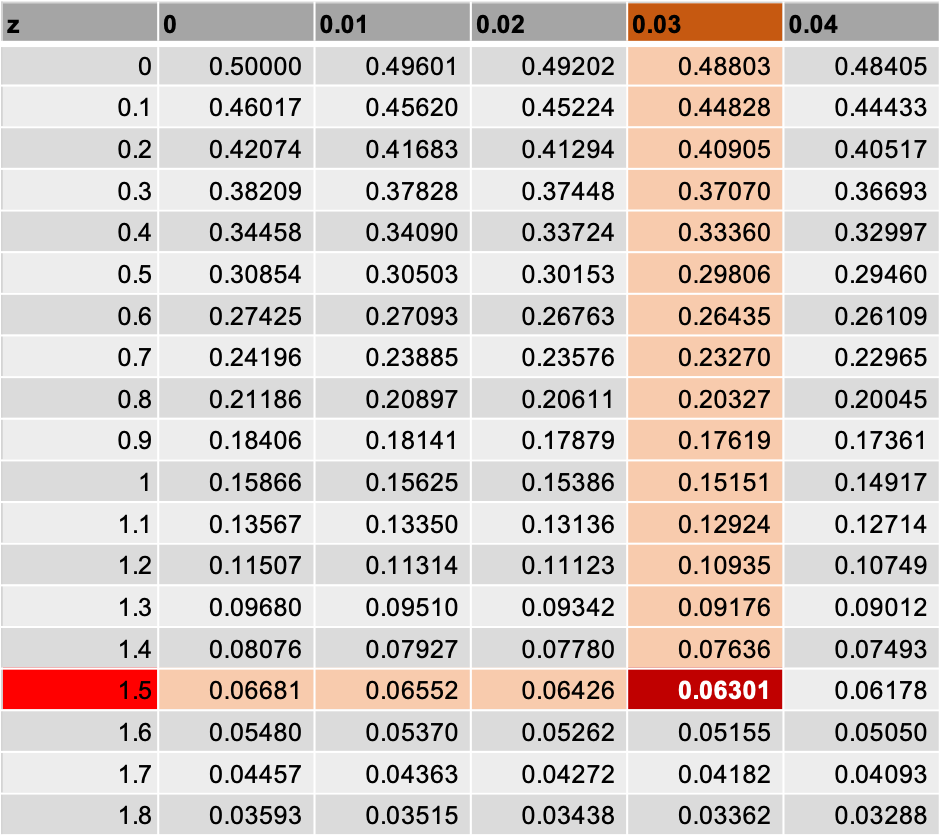
最後に、”二つが交わるところの数値を読み取る”と、確率は0.06301ということがわかります。
0.06301を%に直すと、約6.3% ですね。
標準正規分布表の使い方:実際に使って問題を解いてみよう
では、早速この標準正規分布を使って見るために、次のような問題を考えます。
「あなたが、あるテストを受験したとします。あなたは88点の成績を取りました。そのテストの統計結果は平均が50点、標準偏差が10点でした。あなたの得点は上位何%でしょうか?」
この問題は標準化正規分布を使えば簡単に解くことができます!
問題を解くはじめのステップは、データを標準化することです。
1つ目ステップ”データ値xから平均を引く”に従って計算します。
値x − 平均 = 88 – 50 = 38
次に、2つ目のステップ”データ値xから平均を引いた値を、標準偏差で割る”に従って計算します。
(値x − 平均) / 標準偏差 = 38 / 10 = 3.8
この3.8の数字が、あなたがとったテストの点の標準化されたz値です。
この値から、あなたの得点は上位何%でしょうか?を解くために
上の標準正規分表を見ます。
3.8と0なので、0.0007ですね。
つまり、あなたは上位0.07%に相当するということになります。
標準正規分布表の使い方:z値(zスコア)がマイナスのとき
z値がマイナスの値の時はプラスと読み替えて用います。
もう1問を考えてみましょう。同じテストですが、あなたの点数が平均点より低かった時で考えてみます。
「あなたが、あるテストを受験したとします。あなたは45点の成績を取りました。そのテストの統計結果は平均が50点、標準偏差が10点でした。あなたの得点は上位何%でしょうか?」
まずは、同様にデータを標準化します。
1つ目ステップ”データ値xから平均を引く”に従って計算します。
値x − 平均 = 45 – 50 = -5
数字がマイナスになってしまいました。次に、2つ目のステップ”データ値xから平均を引いた値を、標準偏差で割る”に従って計算します。
(値x − 平均) / 標準偏差 = -5 / 10 = -0.5
この-0.5の数字が、あなたがとったテストの点の標準化されたz値ですが、この表には載っていません。
どうすればいいのでしょうか。
ここで、正規分布は左右対称だという点を思い出してください。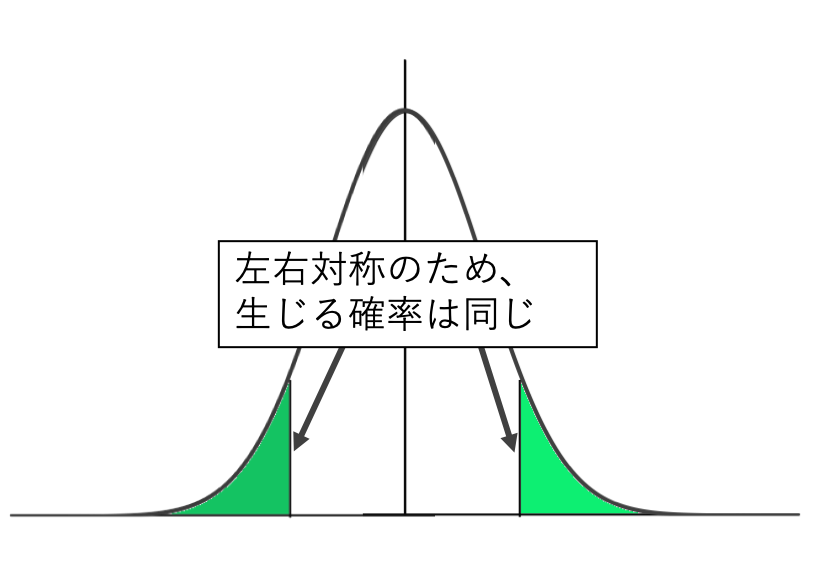
そのため、-0.5は0.5とマイナスをプラスと読み替えます。
すると、標準正規分布表では、0.30584となります。
読み替えたため、下位から0.30584に存在することを意味します。
問題では上位何%かなので、換算するために、次のように計算します。
1 – 0.30584 = 0.69416
よって、答えは0.69416となり、上位約69%になります。
標準正規分布に関するまとめ

- 標準正規分布は、“ある範囲にどれくらいの観測データが含まれているか”を知るのにすごく便利
- どんな正規分布も標準化により標準正規分布に変換することができる
- 標準正規分布表を使うと、”あるz値以上が生じる確率”が何%かが一瞬でわかりる
- z値がマイナスのときはプラスと読み替る












コメント