限られたサンプルの結果から、母集団を推測して、意志決定等に活かすのが推測統計です。
私たちは、t検定や分散分析(ANOVA)を行った結果、平均値に有意な差がみられたとき、母集団レベルでも差があると判断しています。
なぜ、このようなことができるのか。
まだ見ぬ母集団について判断することが許されるのはなぜなのか。
その根底にあるのは「大数の法則」です。
この大数の法則についてわかりやすく解説していきます。
大数の法則とは?

統計に関する初学者向けのテキストでは、紹介されなかったり、軽く触れる程度の扱いにされたりする大数の法則。
推測統計の根幹を支える法則なのですが、数学的に難しいということでそのような扱いを受けているものと思われます。
大数の法則は2種類ある:弱法則と強法則
実は、大数の法則には、2種類あります。
数学的に書くと以下の通り。
![]()
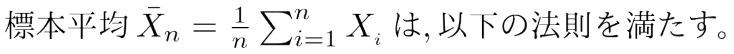
大数の法則1:大数の弱法則
平均μと分散σ2が存在する時、任意の正数εに対して、以下を満たす。
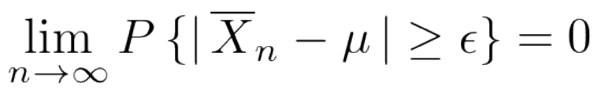
大数の法則2:大数の強法則
平均μが存在する時
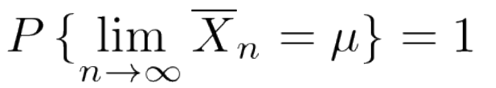
となります。
一見すると難しそうにみえますね。
しかし、大数の法則が数学的に難しいのは、その成立を証明する部分であって
(特に大数の強法則はかなりヘビーです。)
その意味するところを理解することはそれほど難しくはありません。
一つひとつ噛み砕いていきましょう。
大数の法則の意味するところ
確率変数とは、どのような値になるかが確率に依存している変数のことです。
例えば、サイコロを振ると、1, 2, 3, 4, 5, 6のいずれかの目が出ますがどの目が出るかは振ってみなければ分からず(そのたびに変化する)、確率的に決まります。
また、別の例として、企業の健康診断受診者を対象とした糖尿病予備軍に関する研究をするとします。
サンプリングされた受診者の空腹時血糖値がいくつであるかという問題についても、どの受診者がサンプリングされ、どの時点で測定されるかということを考慮すると、測定してみなければ分からず、確率的に決まると言えます。
このように、サイコロの出目やサンプリングされた受診者の血糖値は確率変数になります。
およそ研究対象の個々のあらゆるデータは確率変数と考えて差し支えありません。
次に、サイコロを複数回振る、あるいは複数個を同時に振ることを考えて下さい。
1回目に出た目がいくつであっても2回目に出る目に影響はありません。
(1回目に1が出たからといって、2回目に1が出にくくなったりはしない)
また、健康診断受診者という対象集団からある受診者をサンプリングした場合も、その受診者の血糖値がいくつであれ、別にサンプリングされた受診者の血糖値には影響を与えないと言えます。
(2人が家族であるとか、同じ医療機関であるとかいった場合は別の考慮が必要になることもありますが…)
このような状況を「独立に同一の分布に従う」と言います。
大数の弱法則の解釈
上記条件を前提として、大数の弱法則は、標本数nが十分に大きければ、「独立に同一の分布に従う確率変数」の標本平均と母平均とのズレが一定の値を超える確率が0であるという法則です。
言い換えると、サンプルが大きくなれば、標本平均は母平均に近づいていくということです。(数学的には、標本平均は母平均に確率収束すると言います。)
サイコロの例で考えると、
サイコロは1から6までの目が均等に出現すると考えられるので、その母平均(期待値)は
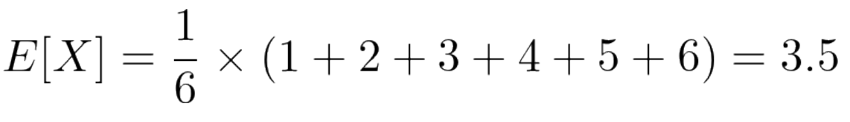
となります。
1コのサイコロを振った場合、どの目が出たとしても3.5になることはありません。
しかし、10コのサイコロを振ったと想像してみましょう。
もちろん、すべてが6になって、標本平均が6となることもあり得ますが極めてまれであることは想像できるかと思います。
さらに、100コのサイコロ、1,000コのサイコロという具合にどんどん数を増やすと考えてみましょう。
そうすると、1から6までの目がおおよそ均等に出ていそうです。その状況で標本平均を計算すると上の3.5に近づいていくことが思い描けるかと思います。
空腹時血糖値の例も同様です。
こちらの場合は確率を想定することは難しいですが、成人男性であれば、その血糖値の母平均は95 mg / dLくらいと思われます。
1人の受診者について計測した場合は平均から大きく離れていることも十分に考えられますが、100人、1,000人と計測する人数を増やしながら標本平均を求めていくと、母平均から大きく離れた値にはなりにくくなっていきます。
大数の強法則の解釈
大数の強法則は、大数の弱法則より少ない条件でより強い結論を導くもので、標本数nが十分に大きければ、「独立に同一の分布に従う確率変数」の標本平均と母平均(期待値)とが一致する確率が1に近づくとなります。
(数学的には、標本平均は母平均に概収束すると言います。)
厳密に確率統計を議論する場合には、両者の違いは大事な話になりますが、ここでは、ほぼ同じことを少し異なる言い方で表現していると思ってもらって問題ありません。
「標本数がどんどん増えていくと標本平均は母平均に近づいていく」
と理解して下さい。
大数の法則を例題とシミュレーションで理解する!
大数の法則のイメージをより確かなものにするために、実際に調査をして確かめてみましょう。
とは言え、実際にサイコロを何万回も振ったり、何万人もの空腹時血糖値を測定したりすることは事実上不可能ですから、Rを使ってシミュレーションしてみます。
大数の法則の例題1:サイコロでのシミュレーション
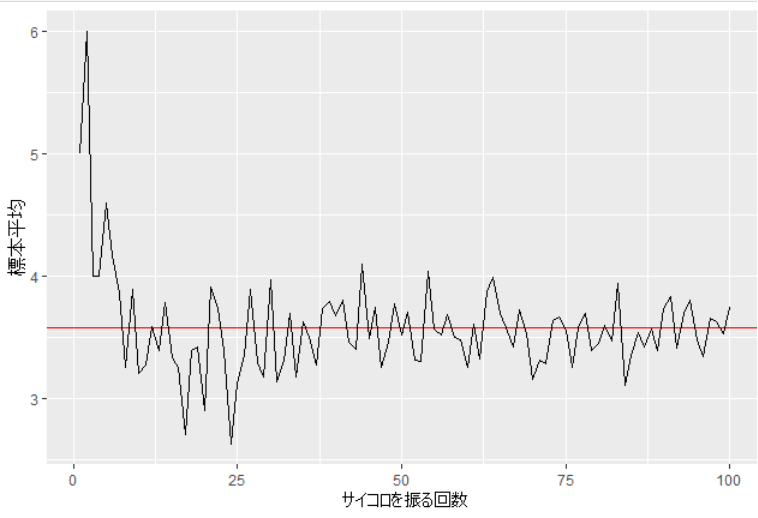
サイコロを1回から100回までそれぞれ振った場合の各標本平均はこうなりました。
振る回数を増やすことで3.5に近づいているように見えますね。
さらに10,000回まで振る回数を増やしてみると以下のようになります。
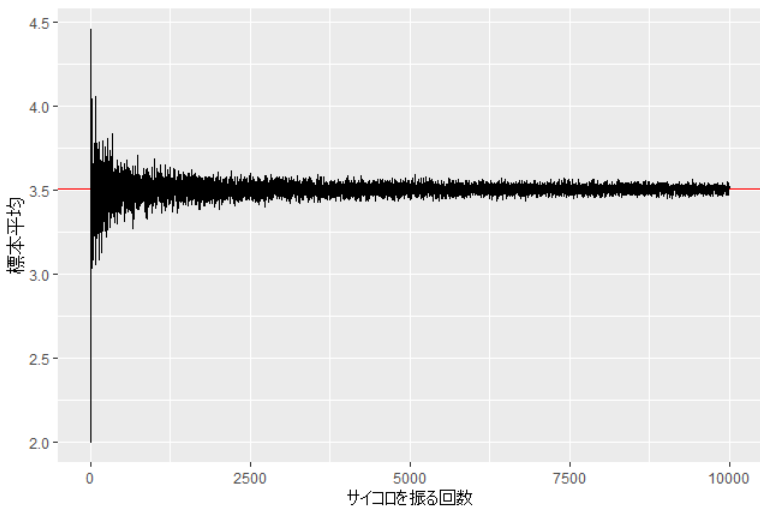
より一層、3.5に近づいていく様子がわかります。
大数の法則の例題2:血糖値でのシミュレーション
成人男性の空腹時血糖値の母平均を95 mg / dL, 母標準偏差20 mg / dLと想定して被験者を増やしていくシミュレーションを行うと
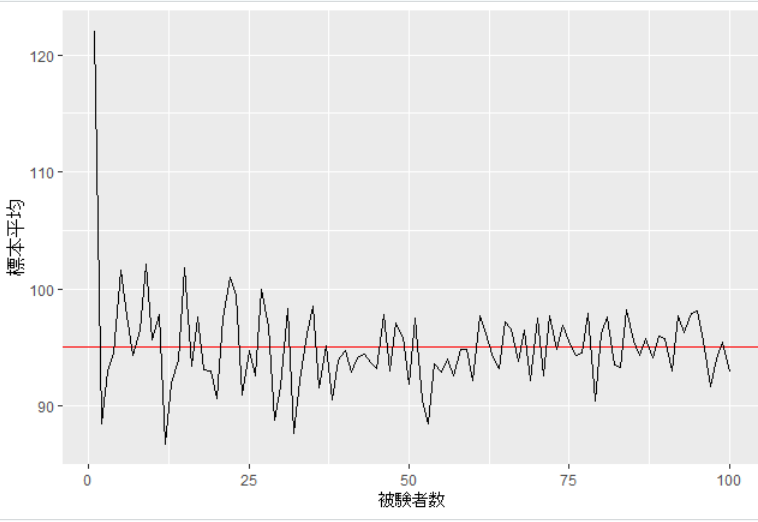
1人から100人までの場合はこのようになりました。
こちらの例でも被験者の数を増やしていくことで標本平均が母平均に近づいていくのが分かります。
さらに10,000人まで増やすと
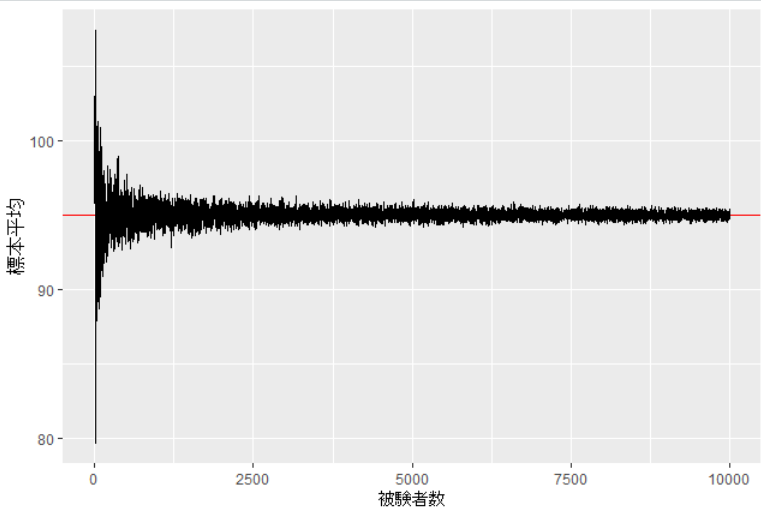
こちらも母平均である95に近づいていくことが分かりますね。
これが大数の法則です。
大数の法則まとめ
大数の法則は、各種の仮説検定や信頼区間による区間推定などの推測統計にとって根幹をなす法則です。
その証明は難解なものかもしれませんが、意味するところをざっくりと言うならば
「サンプル数を十分に増やすと母集団と似てくる」ということになります。
大数の法則は中心極限定理をはじめとする他の多くの定理の土台となるものでもあります。
シミュレーションなどから実感をもって理解しておきましょう。










コメント