帰無仮説とは？対立仮説との違いを例題でわかりやすく。検定で棄却できないときの結論は？

・帰無仮説とはなんのこと・・・？

・対立仮説とは・・・？

・そもそも検定するのになんで仮説が必要なの？

統計の検定といえば、P値が0.05を下回るかどうか。

それだけを考えていませんか？

確かにそれだけ知っていれば、結論の部分は解釈できます。

でも、ちゃんと仮説を知っておくことはすごく大切です。

なぜなら、P値がどういう考えで算出されるかを知ることで、試験のデザインを読み取ることができるためです。

もしあなたが、試験や実験を計画する立場であれば、仮説の理解は必須でしょう。

それほど難しい概念ではないので、是非とも理解しましょう！

帰無仮説と対立仮説を設定する意味：統計学的検定では、差があることを直接証明できない

統計的検定の論理は、少しひねくれています。

どうひねくれているか。

差がないことを否定することによって、差があることを証明する

からです。

つまり、差があることの証拠を見つけるのではなく、差がないことの証拠を見つけることをします。

上記の手続きにより、「差がないことが否定された　→　だから差があるでしょ」ということを言うのです。

ここでいう「差がない」という仮説、そして「差がある」という、2つの仮説があることで、統計学的検定は仮説検定とも呼ばれています。

統計の専門用語では、「差がない」という仮説のことを、帰無仮説と呼びます。

「差がある」という仮説のことを、対立仮説と呼びます。

大枠としてのイメージは、以下のような感じです。

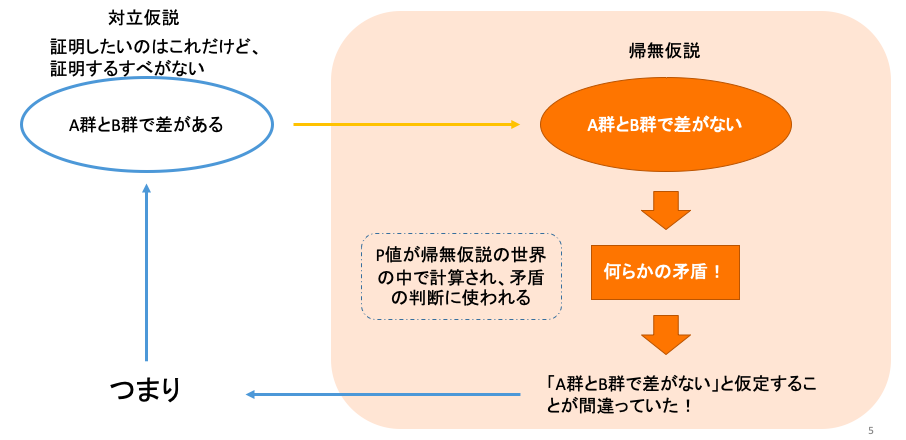
帰無仮説とは無に帰したい仮説のこと

統計的仮説検定でよく見る「帰無仮説」。

文字通り、最終的には「無に帰したい仮説」です。

今回の例では、「犬と人は同じ」や「新薬とプラセボの効果は同じ」が帰無仮説です。

特徴は、本当に示したいことの逆が帰無仮説になる、ということ。

英語ではNull hypothesisと呼ばれます。

対立仮説が証明したい仮説のこと

無に帰したい仮説がある。

じゃあ、本当に証明したい仮説もある、ということですね。

本当に証明したい仮説のことを「対立仮説」と呼んでいます。

英語ではAlternative hypothesisですね。

帰無仮説と対立仮説の例：犬と人は違うって、どうやって証明できる？

ここであなたに問題です。

「犬と人は違う」っていうのはどうやって証明できますか？

（どうやっても何も、見た目が全然違うじゃん・・・）

（何言ってるんだろ・・・）

そんな声が聞こえそうですww

でも、例としてはこれぐらい差がはっきりしているものが良いです。

この例を、統計的な仮説検定に落とし込んでみましょう。

明らかに違いがありそうな犬と人。

でも、証明するって難しいです。

だから、以下のように証明していきます。

手順1：一度、「犬と人は同じ」と仮定する。

一旦、「犬と人は同じ」と仮定するのです。

証明したいのは「犬と人は違う」なのに、一度同じとみなしてみる。

ここがスタートになります。

手順2： 同じと仮定すると矛盾する点を見つける

次に、同じだと仮定すると、矛盾してしまう点を挙げていきます。

例えば、こんなものが考えられますね。

• 2足歩行と4足歩行
• 尻尾の有無
• 全身の毛の有無
• etc…

あなたは、どれだけ挙げられましたか？

手順3：すごく矛盾する点が多いので、 「犬と人は同じ」という仮定が間違っていたのだとする

2番目で、矛盾する点が多くあることに気づきました。

つまり「犬と人は同じ」という仮定をすることが間違っていたのだと気付いたのです。

手順4：以上より、「犬と人は同じ」という仮説を棄却し、「犬と人は違う」という仮説を採択する

これがいわゆる、帰無仮説を棄却し、対立仮説を採用する、ということです。

「帰無仮説を棄却する」というのは、「帰無仮説を考えると矛盾がたくさんあったので、間違いだったとする」ということです。

それを、統計の専門用語で「帰無仮説を棄却する」といっているだけなのです。

帰無仮説と対立仮説の例：犬と人を、新薬とプラセボに置き換えてみる

犬と人の例と同じことを、新薬とプラセボに置き換えてみます。

手順1：一度、「新薬とプラセボの効果は同じ」と仮定する。

手順2：同じだと仮定すると矛盾する点を見つける

例えば、糖尿病の新薬だったら、HbA1cの低下具合の違い。

抗がん剤の新薬であれば、生存率の違い。

これらを、どれだけ新薬とプラセボで違いがあるのかを示します。

手順3：すごく違いが見つかったので、「新薬とプラセボの効果は同じ」という仮説が間違っていたと気付く

手順4：よって、「新薬とプラセボの効果は違う」と結論づける

これが、統計的な仮説検定の大枠です。

理解できましたか？

帰無仮説や対立仮説など、統計用語で置き換えてみる

先ほどの２つの例で挙げた、手順1〜4を、統計用語を使って説明します。

普通の教科書では、ここしか出てきません。

でも今のあなたは、例を理解しています。

スポンジに水が入ってくるような吸水力で吸収できるでしょう。

手順	人と犬の例	統計学的検定
手順1	「人と犬は同じ」と仮定する	帰無仮説を立てる
手順2	「同じ」と仮定すると矛盾する点を見つける	P値を算出し、有意水準より小さいことを示す
手順3	すごく矛盾する点が多かったので、「人と犬は同じ」と仮定することは間違いだったとする	帰無仮説を棄却する
手順4	「人と犬は違う」と結論づける	対立仮説を採択する

これが、統計の専門用語で示した手順1〜4です。

あなたも一度は見たことがあるのではないでしょうか？

帰無仮説を棄却できない時（統計的な有意差が出なかった時）の統計学的検定の結論は？

ここも多くの方がつまずくポイントなので、解説しておきます。

帰無仮説を棄却したら、当然ながら結論は「新薬とプラセボは違う」ということになります。

では、帰無仮説を棄却できない場合の結論はどうなるでしょうか？

多くの方が「新薬とプラセボは同じ」と言える、と勘違いしています。

ですが、これは間違いです。

人と犬の例を考えてみましょう。

人と犬の間に矛盾がそれほど見つけることができなかったとして、「人と犬は同じ」と結論づけられるでしょうか？

無理がありますよね。

言えることは「人と犬は違うと言えるほどの矛盾を見つけられなかった」ということだけです。

これは統計学的検定でも同じです。

つまり、帰無仮説を棄却できなかった時（有意差がなかったとき）の結論は「新薬とプラセボに差があるとは言えない」ということだけ。

決して、「同じ」という結論を導くことはできないので、ご注意ください。

ここは重要なポイントですね。

ここに関しては動画でも解説していますので、ぜひご覧ください！

「同じ」と言いたいなら同等性試験の考え方を使う

検定で有意差がない場合には、「2群間で同じ」という結論はNGであることがわかりました。

じゃあ、「同じ」と言いたい場合はどうすればいいのか？と言いますと、同等性試験の考え方を使う必要があります。

同等性試験は、同等性マージンと95%信頼区間の位置関係把握で解析します。

そのため、まずは同等性マージンを定義する必要があります。

同等性マージンを決めたら、差の95%信頼区間が同等性マージンの中に入っているのか？を確認するのです。

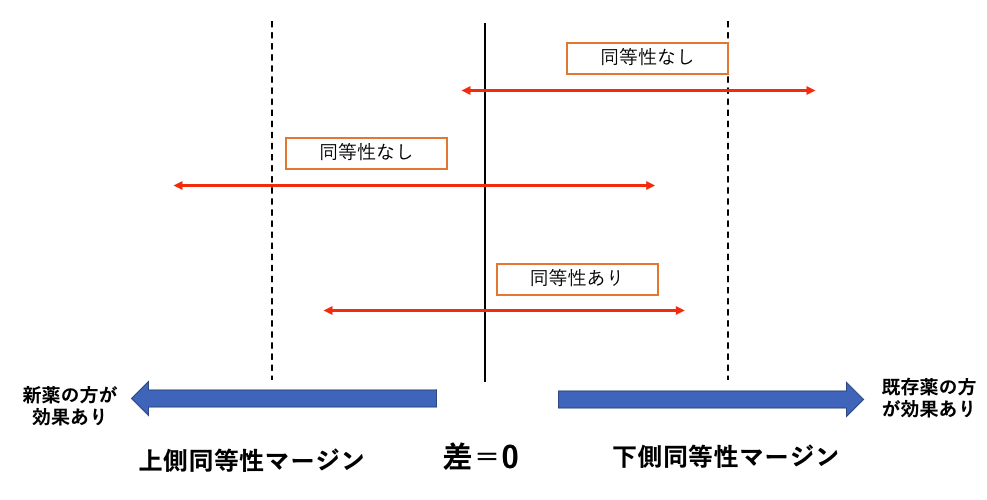
詳しくは「優越性・非劣性・同等性試験の違いは？なぜマージンを使うのか？」という記事でご確認ください！

帰無仮説と対立仮説のまとめ

• 統計学的検定を実施する際には、「帰無仮説」及び「対立仮説」を立てる必要がある。
• 仮説検定とも呼ばれるのが、この２つの仮説を立てるからである。
• 帰無仮説は無に帰したい仮説、対立仮説は採択したい仮説である。

また、動画でも帰無仮説と対立仮説の内容に関してメルマガ読者の疑問について解説していますので、記事と合わせてご確認いただけると理解が進むはずです。

＞＞有意差がないときの結論は？