この記事では「3群比較のサンプルサイズはどう計算する？閉手順の場合と多重性を考慮した検定の場合」としてお伝えしていきます。
2群比較の場合は比較がシンプルですが、3群以上の場合になると、ちょっと複雑になります。
そのため今回の記事では
- 3群以上の比較でのサンプルサイズ計算はどうやればいい？
- 3群以上の比較でのサンプルサイズ計算は多重性を考慮すべき
- 3群比較のサンプルサイズ計算を具体例を用いてフリーソフトEZRで計算してみる
ということをわかりやすくお伝えしますね！
Contents
3群以上の比較でのサンプルサイズ計算はどうやればいい？
サンプルサイズ設計と言えば、通常は2群の試験を想定しています。
プラセボ vs 実薬群、のような状況です。
しかし実際の試験や研究は、2群の比較だけではないですよね。
3群以上の比較をしたい試験や研究も出てくるはず。
そんな場合のサンプルサイズ計算はどうすればいいでしょうか？
3群比較のサンプルサイズ計算では最終的な目的を決めないと決めることができない
3群以上で試験を実施した場合に何が一番の問題になるかというと、「比較できる部分が複数箇所出てくる」ということです。
プラセボ vs 実薬群、のような2群比較であれば、プラセボ vs 実薬群という比較しかやり用がありません。
しかし例えば「プラセボ vs 低用量 vs 高用量」で試験を実施したとき、比較は4通り考えることができます。
- 「プラセボ vs 低用量 vs 高用量」の3群の中でどこかに差がある、という分散分析的な比較
- 「プラセボ vs 低用量」の比較
- 「プラセボ vs 高用量」の比較
- 「低用量 vs 高用量」の比較
上記の4通りの比較に対して、どこが一番重要な結果になりうるのかを考えない限り、サンプルサイズ計算ができません。
そして4通りの比較が考えられるため、場合によっては多重性の問題への考慮も必要になります。
そのため、3群以上のサンプルサイズ計算をする前に、以下の2つのことを考えておく必要があります。
まずは上記2つのことを決めましょう。
3群以上の比較でのサンプルサイズ計算は多重性を考慮すべき
上述の通り、3群以上の比較では多くの場合に多重性の問題が発生します。
そのため、対処すべきか・対処するならどんな方法を用いるのか、を考えなければいけません。
例えば、「プラセボ」「低用量」「高用量」の3群に対して、「プラセボ vs 低用量」「プラセボ vs 高用量」の2つの検定をしたい。
その場合には、主に2つの方法があります。
閉手順の場合のサンプルサイズ計算
検定に順番をつける場合、通常は「最も大事な比較」か「理論的に考えて有意になりやすい順番」を考えていきます。
「プラセボ」「低用量」「高用量」の3群であれば、理論的に考えて「プラセボ vs 高用量」の比較が有意差が出やすく、「プラセボ vs 低用量」の比較は相対的に有意差が出にくいと考えられます。
そのため、「プラセボ vs 高用量」の比較を最初に実施し、有意差が出た場合に「プラセボ vs 低用量」の比較を実施すればOK。
ではこの場合のサンプルサイズ計算では、どのように計算するでしょうか。
考え方に正解はないですが、考え方の一つとしては「サンプルサイズが多くなるように設定する」ということ。
「プラセボ vs 低用量」の比較の方が有意差が出にくいと考えられるのであれば、「プラセボ vs 低用量」の比較の方がサンプルサイズが多く必要になる。
なので、「プラセボ vs 低用量」の2群の比較でサンプルサイズを計算します。
この場合、有意水準は0.05でOKです。
そして、計算の結果として1群あたりの必要症例数が出ますので、それを高用量群でも同じだけ集める、とすればいいのです。
なのでまとめると、以下の通りになります。
- 有意になりにくい比較を考える
- その比較に対して2群の比較のサンプルサイズ計算を実施する
- 得られた1群あたりの症例数を、残りの群でも同じだけ集めるとする
「プラセボ vs 高用量」のサンプルサイズ計算をしていないじゃないか！と思われるかもしれませんが、厳密に計算すると、サンプルサイズは群間でアンバランスになります。
そうなると、症例を群間に割り当てる（ランダマイズさせる）場合にかなり煩雑になります。
そのため、群ごとに全て同じ症例数にすることで試験を円滑に進めることができますし、必要なサンプルサイズを確保できるのでOKということになります。
多重性を考慮した検定を用いる場合のサンプルサイズ計算
次に、多重性を考慮した検定を用いる場合のサンプルサイズ計算です。
こちらも考え方に正解はないですが、考え方の一つとしては「サンプルサイズが多くなるように設定する」ということ。
重性を考慮した検定を用いる場合で、一番厳しい方法（有意差が出にくい方法）は、ボンフェローニ法です。
そのため、ボンフェローニ法を考えて症例数設計をすればOKです。
ボンフェローニ法とは、有意水準を検定の数で割る、というアイデアです。
そのため、「プラセボ vs 低用量」「プラセボ vs 高用量」の2つの検定をしたい場合には、各検定の有意水準を0.05/2=0.025とすればOKということになります。
なのでまとめると、以下の通りになります。
- 有意になりにくい比較を考える
- 有意水準をボンフェローニ法で考え、2群の比較のサンプルサイズ計算を実施する
- 得られた1群あたりの症例数を、残りの群でも同じだけ集めるとする
3群比較のサンプルサイズ計算を具体例を用いてフリーソフトEZRで計算してみる
それでは実際に、EZRで3群比較のためのサンプルサイズ計算を実施してみます。
具体的な数値を仮定しないとサンプルサイズ計算はできないため、以下の状況を想定します。
- アウトカムは連続量
- 「プラセボ vs 低用量」の平均値の差は5であり、「プラセボ vs 高用量」の平均値の差は7である。
- 群間差のSDはどちらの比較でも10である。
- 検出力は80%
- 有意水準は0.05
そしてこの状況に対して、
のそれぞれの場合に分けてみますね。
閉手順の場合のサンプルサイズ計算をEZRで実施する
閉手順の場合のサンプルサイズ計算の手順は以下の通りでした。
- 有意になりにくい比較を考える
- その比較に対して2群の比較のサンプルサイズ計算を実施する
- 得られた1群あたりの症例数を、残りの群でも同じだけ集めるとする
今回の場合、有意になりにくい比較は「プラセボ vs 低用量」の平均値の差は5である状況なので、この場合のサンプルサイズ計算を実施します。
ここのサンプルサイズ計算は、通常のEZRで2群のサンプルサイズ計算と同じ。
「統計解析」→「必要サンプルサイズの計算」→「2群の平均値の比較のためのサンプルサイズの計算」の順に選択していきましょう。
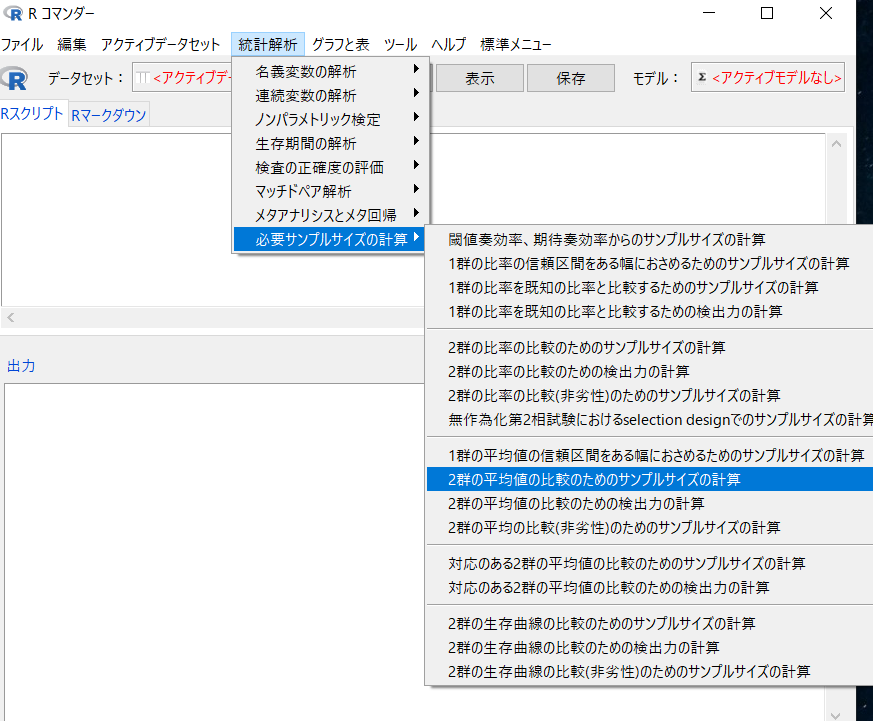
そして、平均値の差が5、SDが10、検出力は80%、有意水準は0.05でしたので、以下の通り入力します。
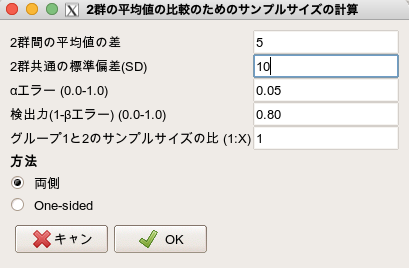
そしてOKを押すと、1群あたり63例必要であることがわかりました。
そのため、残りの高用量群でも63例必要として、試験全体では63*3=189例必要だ、という計算結果になります。
多重性を考慮した検定を用いる場合のサンプルサイズ計算をEZRで実施する
多重性を考慮した検定を用いるの場合のサンプルサイズ計算の手順は以下の通りでした。
- 有意になりにくい比較を考える
- 有意水準をボンフェローニ法で考え、2群の比較のサンプルサイズ計算を実施する
- 得られた1群あたりの症例数を、残りの群でも同じだけ集めるとする
今回の場合、有意になりにくい比較は「プラセボ vs 低用量」の平均値の差は5である状況なので、この場合のサンプルサイズ計算を実施します。
ここのサンプルサイズ計算は、通常のEZRで2群のサンプルサイズ計算と同じ。
「統計解析」→「必要サンプルサイズの計算」→「2群の平均値の比較のためのサンプルサイズの計算」の順に選択していきましょう。
そして、平均値の差が5、SDが10、検出力は80%、有意水準は0.025でしたので、以下の通り入力します。
有意水準が0.025であるのは、今回の比較が2つであり、ボンフェローニ法だと0.05/2=0.025で1つ1つの検定を実施するから、という理由です。
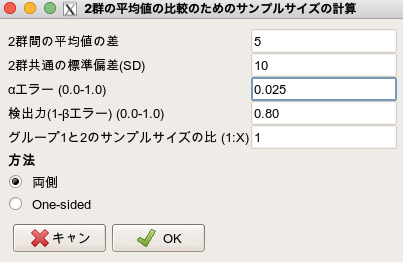
そしてOKを押すと、1群あたり77例必要であることがわかりました。
そのため、残りの高用量群でも63例必要として、試験全体では77*3=231例必要だ、という計算結果になります。
まとめ
いかがでしたか？
この記事では「3群比較のサンプルサイズはどう計算する？閉手順の場合と多重性を考慮した検定の場合」としてお伝えしました。
3群以上の比較になると比較する部分を複数考えることができてしまうため、まずは「最終的にどのような比較をしたいのか」ということが大事です。
それが整理できれば、あとは2群の比較のサンプルサイズ計算を応用すればいいだけでしたね。
第1章：臨床研究ではなぜ統計が必要なのか？計画することの重要性
第2章：研究目的をどれだけ明確にできるのかが重要
第3章：p値で結果が左右される時代は終わりました
第4章：多くの人が統計を苦手にする理由
第5章：統計を使えるようになるために今日から何をすれば良いか？
第6章：統計を学ぶために重要な環境
もしあなたがこれまでに、何とか統計をマスターしようと散々苦労し、何冊もの統計の本を読み、セミナーに参加してみたのに、それでも統計が苦手なら…
私からプレゼントする内容は、あなたがずっと待ちわびていたものです。
