サンプルサイズの決め方は？臨床研究で統計的な検出力を保持する計算式

2025年2月25日

突然ですが、臨床研究でのサンプルサイズの決め方を知っていますか？

統計学的検定をする際にとても重要なこと。

それが、サンプルサイズを事前に決めることです。

なぜかというと、統計学的検定とは、事前に検出力を保った上で検定する必要があるから。

そうでなければ、いくらP値が0.05を下回ったところで、有意差が出たというその結果は「たまたま」にしか過ぎないからです。

今回の記事では、なぜサンプルサイズを決めなければならないのか、そして、サンプルサイズを決めるには何を意識すれば良いのか、論文の書き方についてお伝えします。

＞＞もう統計で悩むのは終わりにしませんか？

↑1万人以上の医療従事者が購読中

臨床研究でのサンプルサイズの決め方は？なぜ必要症例数は事前に決めなければならないの？

サンプルサイズは、事前に決める必要があることをお伝えしました。

しかし、なぜ事前に決めなければならないのか？という疑問が出てきますよね。

そのために、T検定を例にしてなぜ事前に決めなければならないのかを解説します。

サンプルサイズが大きいとP値が小さくなる：T検定を例にして計算式を理解する

T検定でやっていることは、以下の4つの手順です。

プラセボ群や実薬群の平均値、標準偏差を算出する
T統計量を算出する
P値を算出する（T統計量が大きいと、P値は小さくなる）
P値が有意水準（α=0.05）を下回っているかどうかを判断する

この時、T統計量がどんな計算式で求められるかを確認してみます。

T統計量とは、以下の式です。（Nがサンプルサイズ、SDが標準偏差を示しています）

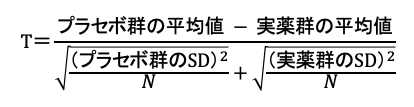
この時、プラセボ群のSDと被験薬群のSDが同じと仮定し、式展開してみます。

すると、以下のような式になります。

この式を見ると、3つのことに気づきます。

サンプルサイズ（N）を大きくすると、T統計量が大きくなる（つまり、P値が小さくなる）
群間の差が大きいと、T統計量が大きくなる（つまり、P値が小さくなる）
標準偏差（SD）が小さいと、T統計量が大きくなる（つまり、P値が小さくなる）

そう、P値が小さくなる要素は、群間の差が大きいだけじゃないんです。

サンプルサイズが大きくても、P値は小さくなります。

サンプルサイズを事前に決めないとなぜP値が小さくなったかわからなくなる

そのため、サンプルサイズを事前に決めなかった場合に、有意差が出た時。

2つの解釈ができることになります。

群間の差が大きくてP値が小さくなった可能性
サンプルサイズが大きくてP値が小さくなった可能性

私たちが得たいのは、1の「群間の差が大きくてP値が小さくなった」という結果です。

しかしながら、サンプルサイズを事前に決めておかないと、P値が小さくなった要因が「群間差がある」と「サンプルサイズが大きい」の2つの可能性が残ってしまうことになってしまうのです。

そのため、サンプルサイズを事前に決める理由をまとめます。

P値が小さくなった時に、「群間差があってP値が小さくなった」のか「サンプルサイズが大きいためにP値が小さくなったのか」の2つの可能性が残ってしまうため

これはぜひ理解してください。

サンプルサイズの決め方は？検出力を確保するために考えること

サンプルサイズを事前に決めておく重要性を理解しました。

ということで、サンプルサイズの決め方です。

サンプルサイズを決めるためには、4つを決める必要があります。

群間の効果の差
ばらつき
αエラー
βエラー

逆にいうと、上記の4つを決めてしまえばサンプルサイズは自動で決まります。

そのため、この4つに症例数を加えた5つを五角形に見立てて、症例数を決めるペンタゴンという場合があります。

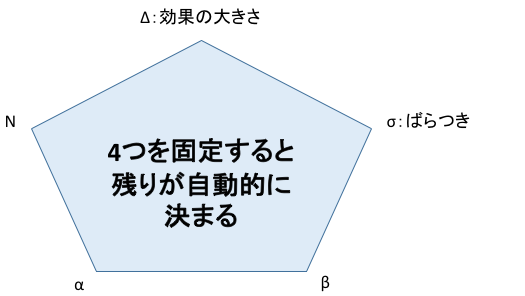
サンプルサイズが変動する要因は？検出力を保つために

群間の効果の差、ばらつき、αエラー、βエラーの4つを動かせば、サンプルサイズが変動することがわかりました。

では、各4つの要素をどう動かすと、サンプルサイズが多くなるか、を見てみます。

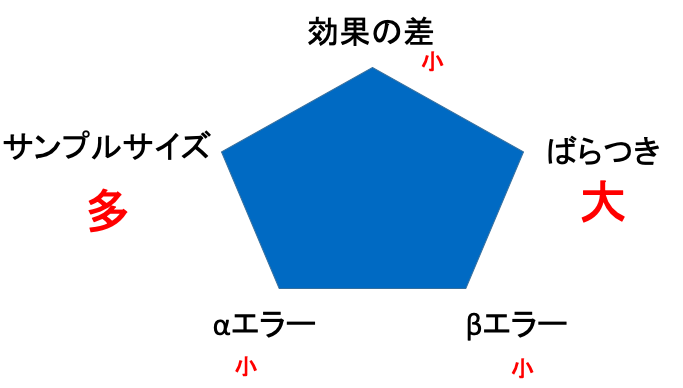
群間の効果の差が小さいと、サンプルサイズは多くなる
ばらつきが大きいと、サンプルサイズは多くなる
αエラーが小さいと、サンプルサイズは多くなる
βエラーが小さい（検出力が大きい）と、サンプルサイズは多くなる

このような動きになります。

上記の4つの動きに関しては、絶対に覚えておきましょう。

丸暗記でもいいぐらいです。

ちなみに、βエラーに関しては、検出力で表現する場合があります。

検出力とは（1-βエラー）で表現できるため、βエラーが小さいというのは、検出力が大きい、と等しいことです。

サンプルサイズの決め方は、薬の開発状況によって変わる

サンプルサイズを決めるのは、群間の効果の差、ばらつき、αエラー、βエラーの4つでした。

そして、それぞれが変化すると、サンプルサイズが大きくなったり小さくなったりします。

では、開発費用や開発期間が限られた中で、サンプルサイズをできるだけ小さくするには、どこをどうすれば良いでしょうか？

それは、その薬の開発状況に応じて変化させる必要があります。

第III相試験であれば、αエラーは5%以下にしなければならないと明確に決まっているため、αエラーを変えることが出来ません。

しかし第II相試験であれば、企業リスクを受け入れる形で、αエラーを10%にしてみることも可能です。

ですがやはり一番に考えるのは、薬効の効果の差と、そのばらつきを変えることが出来ないか？ということです。

薬効の効果の差を大きくするためには、試験に組み入れる患者を、薬剤が効く集団に限定するように、組み入れ基準や除外基準を決めるということを考えます。

しかし、薬が効く集団だけで試験をするとなると、母集団がどこになるのか、そして一般化可能性を考える必要があります。

そうして限定された集団で試験をすると、薬として発売されたとしても投与できる集団が限定されて、結局売り上げが伸びないといったことにつながる可能性が出てきます。

このように、開発コストの面と、一般化可能性の面を天秤に掛けて、常に試験の集団を考えなければいけません。

＞＞もう統計で悩むのは終わりにしませんか？

↑1万人以上の医療従事者が購読中

論文にもサンプルサイズをMethodに記載する。書き方は？

サンプルサイズが事前に決まっているかどうか、論文ではMethodを読むことで確認することが出来ます。

ここでサンプルサイズのことが書いていない論文については、どれだけ素晴らしい結果（P値が小さい結果）であろうと、たまたま出た結果であることが否定できません。

つまり、その試験をもう一度実施したら、全く違った結果が出る可能性があるということです。

なぜなら、前述の通り、本当に薬に効果があったためにP値が小さくなったのか、サンプルサイズが大きかったためにP値が小さくなったのかが分からないためです。

そして、あなたの研究でもサンプルサイズを記載する必要があります。

サンプルサイズの論文への書き方に関しては、他の論文を参考にすることでOK。

例えば、こちらの論文を見てみます。

DOI: 10.1056/NEJMoa2203094

Methodを見ると、下記のようなサンプルサイズ計算の記載があります。

We estimated that 25% of the patients in the acetazolamide group would have successful decongestion within 3 days after randomization; 25% was chosen to represent a clear, meaningful absolute benefit of 10 percentage points as compared with placebo. Assuming a two-sided alpha of 0.05 and a statistical power of 80%, we calculated the targeted sample size for the trial to be 494, and to account for a potential withdrawal of 5% of the patients, we calculated that the trial would need to enroll 519 patients.

サンプルサイズ計算をしていれば、その通りに記載すればいいのですが、探索的な研究の場合には事前にサンプルサイズ計算をしていない場合もあるはず。

事前にサンプルサイズ計算をしていない場合でも、Methodにはその旨を記載します。

例えばこちらの論文を参考にしてみます。

https://doi.org/10.1111/bjd.14207

Methodを見ると、下記のようなサンプルサイズ計算の記載があります。

No statistical sample size calculations were conducted. However, a sample size of nine patients per group gave post hoc powers of 43%, 40% and 31% to detect differences in mean of 30%, 29% and 25%, respectively, for pruritus VAS score at week 4, assuming a common SD of 33%, using a two‐group t‐test with a two‐sided significance level of P < 0·05 for percentage change from baseline between placebo and each active group.

最初に「No statistical sample size calculations were conducted.」と、潔く記載していることがわかります。

そして、事前にサンプルサイズ計算をしていない代わりに、事後的な検出力を計算して記載しています。

このような書き方もOKです。

＞＞EZRで検出力計算をするには？