統計での分散には、”nで割る分散”と”n-1で割る分散”の二種類があります。
“nで割る分散”は、一般的な分散です。
“n-1で割る分散”を不偏分散と呼びます。
この記事では、
- 一般的な分散と不偏分散では何が違うのか。
- どうして、不偏分散はn-1で割る必要があるのか。
- 分散と不偏分散の使い分け方
ついて説明していきます。
不偏分散と標本分散の違いは？n-1で割る理由
まずは、標本分散と普遍分散の違いについて。
- 標本分散：データのバラツキを表すために用いられる
- 不偏分散：標本から母集団の分散を推定するために用いられる
そして分散には母分散と標本分散があります。
“標本分散”と”不偏分散”の違いを理解するためには、まず、母集団と標本の性質について知る必要があります。
不偏分散を理解するのに必要な母集団と標本とは？
母集団と標本の意味は以下のようです。
- 母集団は“知りたい対象のすべて”を指します。
- 標本は“知りたい対象の一部”を指します。
母集団と標本の関係性は意味は以下のようです。
- “知りたい対象のすべて”を調べるために、“知りたい対象の一部”を調べることを”抽出“と言います。
- “知りたい対象の一部”から”知りたい対象のすべて”を予測することを”推定“と言います。
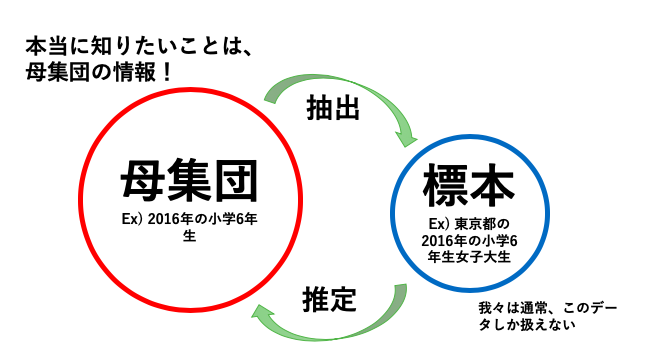
詳しくは、母集団と標本の関係とはでも説明しています！
“標本分散”と”不偏分散”が使われるのは、母集団から抽出した標本の性質に由来します。
不偏分散がn-1で割る分散
母集団と標本の関係には
“母集団の性質と、母集団から抽出した標本の性質は一緒ではない”という性質があります。
母集団の、平均、分散、標準偏差と、
標本の、平均、分散、標準偏差は、
一致するとは限りません（偶然一致することはあります）。
そのため、統計学では母集団と標本の統計の値は区別して考えられています。
統計学では母集団と標本の統計の値は区別して考えるため、
母集団の分散を母分散、
標本の分散を標本分散と呼びます。
標本分散は、式ではこのように書きます。
多くの調査や研究は、母集団の性質を明らかにするが目的で行われています。
しかし、母集団を調査することは、コストや技術的に不可能なことが多いです。
そこで、標本から母集団を推定する必要が生まれます。
標本から母集団の分散を推定するために、不偏分散が用いられます。
不偏分散は、式ではこのように書きます。
(観測データ-1)と、データ数から1を引くのが標本分散との違いです。
これが俗にいうn-1の分散。
ここまでの話をまとめると、
- 母集団の分散を母分散という
- 標本の分散を標本分散という
- 標本から母集団の分散を推定した分散を不偏分散という
不偏分散の名前の由来：分散の不偏推定量だから
不偏分散という名前は、不偏分散分散の不偏推定量であることに由来します。
標本から母集団の性質を推定するために、不偏推定量というものが用いられます。
不偏とは、漢字の通り、”偏りのないもの”という意味です。
統計学には、“平均的に過大にも過少にも推定していない”という意味です。
“母集団の性質と、母集団から抽出した標本の性質は一緒ではない”という性質により、
標本の性質は、母集団と比べたとき、偏りが生じてしまいます。
この偏りを補正することで、母集団の性質を推定したものを不偏推定量といます。
どうして、不偏分散はn-1で割るのか？
不偏分散で、n-1で割るのは”偏り”を補正するためです。
先ほど、”母集団の性質と、母集団から抽出した標本の性質は一緒ではない”と説明しました。
これは、標本の性質は、母集団の性質と比べてからみて”偏り”といえます。
不偏分散で、n-1で割るのはこのかたよりを補正するためです。
具体的には、
標本分散は母分散よりも小さくなるという性質に由来します。
これを防ぐために、n-1で割ります。
1を引くと分母が小さくなるので、分散は少し大きくなります。
不偏分散から不偏標準偏差へ：注意してほしいこと
不偏〇〇というのは、母集団の性質の不偏推定量と上で説明しました。
そのため、不偏標準偏差を母集団の標準偏差（母標準偏差）として定義します。
しかし、多くの文献やネットの情報では、
“不偏分散の平方根”を、不偏標準偏差として定義していますが、
これは誤用なので気をつけてください。
正しい不偏標準偏差は、“不偏分散の平方根を補正した値”です。
“不偏分散の平方根”は“不偏分散の平方根”や”不偏分散平方根”として定義されています。
しかし、Excelなどでは、“不偏分散平方根”の計算が用いられており、名称以外はそこまで意識する必要はありません。
不偏分散と標本分散はどちらを使うべき？
- データの分散が知りたいとき：分散（標本分散 or 母分散）
- データから母集団の性質を推定したいとき：不偏分散
母集団の推定が目的のときは、不偏分散を用います。
クラスのテストの結果など、母集団のデータが揃っている場合は、分散を用います。
標準偏差のときは
- データの標準偏差が知りたいとき：標準偏差（標本標準偏差 or 母標準偏差）
- データから母集団の性質を推定したいとき：不偏標準偏差 or 不偏分散平方根
標準偏差と分散の関係については、こちらの記事をご覧ください！
不偏分散を求めるのにエクセルでの関数は？
最後に、エクセルで分散または、不偏分散または不偏標準偏差を用いる時に使う関数について紹介します。
分散と不偏分散
| 分散（標本分散 or 母分散） | VAR.P |
| 不偏分散 | VAR または VAR.S |
標準偏差と不偏標準偏差または不偏分散平方根
| 標準偏差（標本標準偏差 or 母標準偏差） | STDEV.P |
| 不偏標準偏差 | 該当なし |
| 不偏分散の平方根 | STDEV または STDEV.S |
まとめ
- 母集団の分散を母分散という
- 標本の分散を標本分散という
- 標本から母集団の分散を推定した分散を不偏分散という
- 不偏分散で、n-1で割るのは”偏り”を補正するため
コメント