・変動係数って初耳なんだけど、これって何?
・変動係数の計算方法は?
・変動係数はどういう時に使えるの?
今日は変動係数(CV値)について!
例を使ってわかりやすく説明します。
変動係数は、ばらつきを表す指標の一つ。
だけど、分散とか標準偏差よりマイナー。
なぜなら、データを見る上で「変動係数がないとどうにもならん」という状況がないからですね。
だから知名度が低い。
変動係数が記載されていない教科書もありますしね。
でも、変動係数を知ると、いろんなことが分かるようになります!
では、一緒に学んでいきましょう!
変動係数(CV値)とは?わかりやすく解説!

マイナーな変動係数(CV値)。
いまいちどうやって使うかわからない。
そのため今日は、変動係数(CV値)を知ることでどんなことを知ることができるか。
そんなメリットを先に話しておこうと思います。
こんな状況ありませんか?
- AとBの測定機器の精度を比べたい時
- CとDの会社の売上状況を比べたい時
- EとFの株のリスクを比べたい時
こんな時、変動係数の出番です!
共通していることは「比べたい時」に変動係数が有効だということ。
つまり、変動係数が一つあるだけでは、特にそこから何も見いだすことができないんです。
2つ以上の変動係数があって初めて、その値に意味が出てきます。
変動係数(CV値)の定義は驚くほど簡単!使うのは平均値と標準偏差
変動係数の計算方法は、かなり簡単です。

これは、誰でも計算できますよね。
めちゃめちゃ簡単です。
でも、重要なのはここから。
変動係数でつまずくのもここからです。
変動係数(CV値)の式からわかる意味:〇〇がなくなる

標準偏差を平均値で割ると、あるものが無くなります。
あなたは答えられますか?
例として、体重の変動係数を考えてみましょう。
体重の単位はkgです。
では、体重の平均値の単位はどうですか?
これもkgですね。
じゃあ、体重の標準偏差の単位はどうでしょうか?
実はこれもkgです。
ということは、変動係数は標準偏差を平均値で割ったもの。
kgをkgで割るので、「単位なし」になります!
変動係数には単位がない!
これが重要な特徴です!
変動係数(CV値)に単位がないことがなぜそこまで重要か
単位がないことで、めちゃくちゃ便利になることがあります。
覚えていますか?
変動係数が有効な場面。
どんな時に変動係数は有効利用できるのでしたでしょうか?
そう、比較する時ですね。
単位がなくなると「どんなスケール、どんな単位であっても比較可能」になります。
標準偏差ではそうはいかないですね。
体重の標準偏差と、身長の標準偏差を比べる。
そんなのできません。
だって、kgとcmの比較ですから、そんなものに意味はありません。
ですが、体重の変動係数と、身長の変動係数を比べる。
これは可能です。
比較した先にどんな利用方法があるのかはさておき、比較自体は可能になります。
もっと現実的な例。
ある日本企業の株と、あるアメリカ企業の株を比較したい。
日本企業の株を10日間追跡した時の標準偏差は100でした。
この時、あなたは2つの株を比較できるだろうか?
答えはNoです。
だって、単位が違うから。

日本の株の単位は、円。
アメリカの株の単位は、ドル。
どうやっても比較できない。
これを変動係数に直すと、比較できるようになります。
だって、単位がないから。
単位がないことで、同じ土俵で比較ができるようになります。
これ、めちゃめちゃ便利じゃないですか?
変動係数(CV値)の使い方を例で学ぶ
では、3つの例から変動係数の理解を深めていきましょう。
- AとBの測定機器の精度を比べたい時
- CとDの会社の売上状況を比べたい時
- EとFの株のリスクを比べたい時
変動係数(CV値)の利用例1:測定機器の精度を比べてみる
こんな状況はないですか。
試作品Aと試作品Bの体重計の測定精度を比較したい。
こんな時に、変動係数が使えます。
まずは、単位の確認。
AのデータもBのデータもどっちもkgですね。
なので、同じ人がAにもBにも乗れば、標準偏差でも比較可能です。
でもなんらかの制限により、以下のような状況でしか比較できなかったら。
Aではある男性の体重を10回測定する。
Bではある女性の体重を10回測定する。
この時に、標準偏差で比較していいですか?
悩みますね。
だって、スケールが違うから。
ここでいうスケールとは、平均的な体重、と思ってもらえればOKです。
男性と女性では、明らかに女性の方が軽い。
そのため、一概に標準偏差では比較するのは難しそうです。
そして、以下のような結果が出たとします。
| 平均 | 標準偏差 | |
| 体重計A | 60kg | 0.5kg |
| 体重計B | 45kg | 0.5kg |
「標準偏差が同じだから、AもBも同じぐらいの測定誤差を持っている!」
と結論づけるのは間違いですね。
というのも、予想通り平均値が違うのでスケールが違う。
この場合には、変動係数です。
Aの変動係数:0.5/60=0.008
Bの変動係数:0.5/45=0.011
「Aの変動係数<Bの変動係数」
でした。
つまり、Aの体重計の方が測定誤差は小さいと言えます。
変動係数(CV値)の利用例2:会社の売上状況を比べる時
今度は、C社とD社の売上を比べてみます。
昨年一年間の、月あたりの平均売上とその標準偏差が以下の通りだったとします。
| 平均 | 標準偏差 | |
| C社 | 100億円 | 100億円 |
| D社 | 1億円 | 1億円 |

C社の標準偏差が大きいから、月あたりの売上の変動はC社が大きい?
でも待てよ、D社は標準偏差が小さいけど、平均の売上も小さいぞ。
こんな時、あなたには思い出して欲しい。
変動係数の存在を!!
C社の変動係数:100億/100億=1
D社の変動係数:1億/1億=1
そう、変動係数はどちらも同じ。
つまり、月あたりの売上の変動はどちらも同じなのです。
C社は、D社の規模を大きくしたような会社、ということができます。
変動係数(CV値)の利用例3:株のリスクを比べる時
もう、お腹いっぱいと思われそうですが、最後にもう一つ。
日本の会社E社と、アメリカの会社F社の株を比較したい時。
1ヶ月前の株価の平均と標準偏差が以下のようだったとします。
| 平均 | 標準偏差 | |
| E社 | 5000円 | 100円 |
| F社 | 100ドル | 10ドル |
E社とF社では、通貨も違う上に、スケールも違う。
こんな状況で、あなたはどのように投資先を決めますか?

こんな時にも思い出して欲しいのです。
標準偏差を平均値で割った値を。
そう、変動係数を!
E社の変動係数:100円/5000円=0.02
F社の変動係数:10ドル/100ドル=0.1
E社の変動係数はF社の変動係数よりも小さい。
つまり、株価の変動が相対的に小さいということ。
ここから何が言えるか。
あなたは分かるでしょうか?
こんなことが言えますね。
変動係数が小さいE社への投資は、ローリスク・ローリターン
変動係数が大きいF社への投資は、ハイリスク・ハイリターン
このような結論を出すことができます。
変動係数(CV値)をエクセルではどうやって計算する?
では、エクセルではどのようにして変動係数を出せば良いでしょうか。
残念ながら、変動係数を直接求める関数はありません。
ですが、変動係数の式は難しくなかったですよね。

なので、平均値と標準偏差があればOKです。
ということで、平均は「=average()」で算出できますし、標準偏差は「=stdev.s()」で算出できます。
あとはこれを割るだけですね。
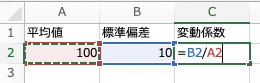
これだけで変動係数を求めることができます!
変動係数(CV値)に関するまとめ

変動係数はバラツキの指標の一つ。
一番の特徴は、単位がないこと。
それにより、単位やスケールによらず複数のデータを比較できる。
一方で標準偏差は、1つのデータの状況を知るのに有用。
変動係数に関して動画でも解説していますので、合わせてご確認いただけると理解が進むはずです。













コメント