この記事では「陽性尤度比と陰性尤度比とは？感度特異度との関係と使い方まで例を交えて解説」ということでお伝えします。
- 陽性尤度比と陰性尤度比の基となる「尤度」とはそもそも何？
- 陽性尤度比と陰性尤度比は何を意味する？
- 陽性尤度比と陰性尤度比の使い方
が理解できるようになります。
陽性尤度比と陰性尤度比は診断研究でとても重要な指標なので、ぜひご覧くださいませ！
Contents
陽性尤度比と陰性尤度比の基となる「尤度」とは？
陽性尤度比と陰性尤度比そのものを解説する前に、そもそも「尤度って何？」ということを整理していきます。
尤度というものは教科書的には
「ある結果（や観測データ）」が得られた時にその結果を生み出す元となるパラメータはどれぐらいだろうか？ということの尤もらしさ
という説明になっています。
・・・私としてはその説明だけだとちょっと良くわからない、、という感じだったので、サイコロの例で尤度を考えてみます。
サイコロの例で尤度を考える
サイコロで1の目が出る確率を考えます。
通常、サイコロで1の目が出る確率は1/6なので、100回サイコロを投げたら16回ぐらいは1の目が出るだろう、ということを考えることができます。
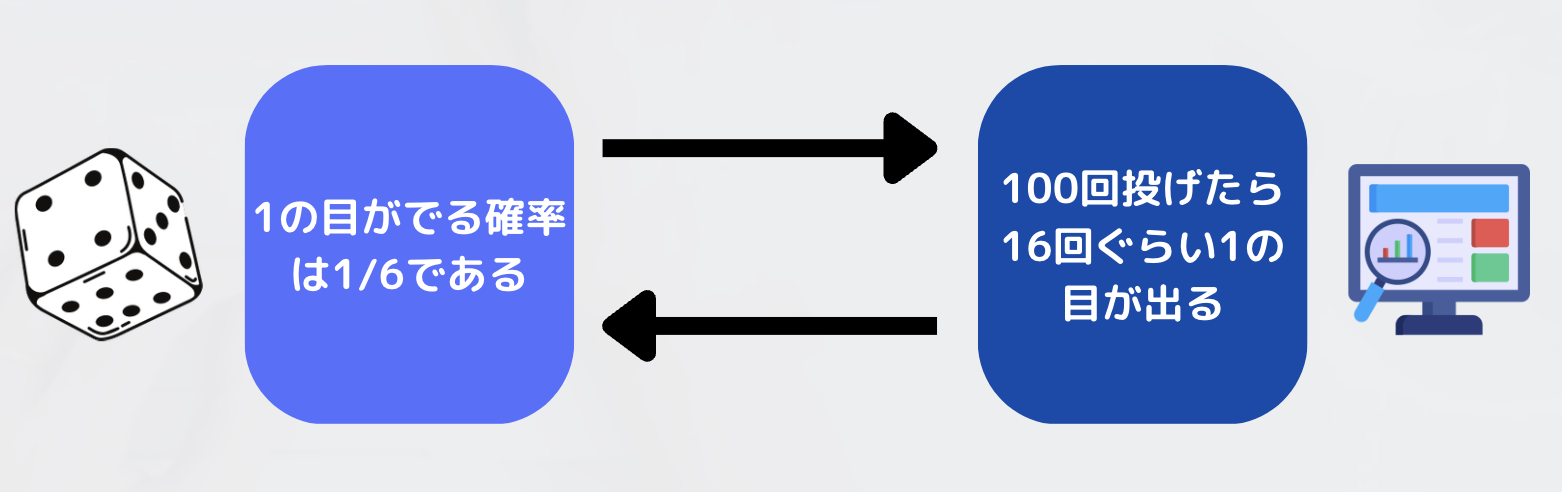
上記の図で言うと、左から右への矢印（→）のことを考えることが通常の確率の考え方、ということになります。
じゃあ尤度はというと、「「ある結果（や観測データ）」が得られた時にその結果を生み出す元となるパラメータはどれぐらいだろうか？ということの尤もらしさ」と言うことだったので、右から左への矢印（←）を考えることが尤度、ということです。
つまり、
- 100回サイコロを投げたら1の目が16回出た
- この結果から、このサイコロの1の目がでる確率（パラメータ）がどれぐらいだろうか？
- きっと、1/6と考えるのが尤もらしいだろう
と考えていくのが、尤度なのです。
なぜそのような尤度を考える必要があるかといえば、世の中の興味ある確率というものは知られていないことが多いからです。
サイコロで1の目が出る確率は1/6であり、コインで表が出る確率は1/2であるというのは周知の事実ですが、このようにわかっていること自体が少ないんです。
例えば
- 私が3年後にがんになる確率
- 咳と鼻水があった時にインフルエンザである確率
というのは、医学的にとても興味あることではありますが、知られているものではないです。
そのため、研究として観測データを取得し、取得したデータをもとに「じゃあその確率はどのぐらいと考えるのが尤もらしいのか？」を考えることが重要になります。
感度と特異度は尤度である
尤度がわかったところで、話を「検査の陽性陰性」と「本当に疾患があるかどうか」という検査に関して考えてみようと思います。
以下の記事にある2×2分割表を考えます。
＞＞感度と特異度の計算方法をわかりやすく！分割表からの求め方を解説！
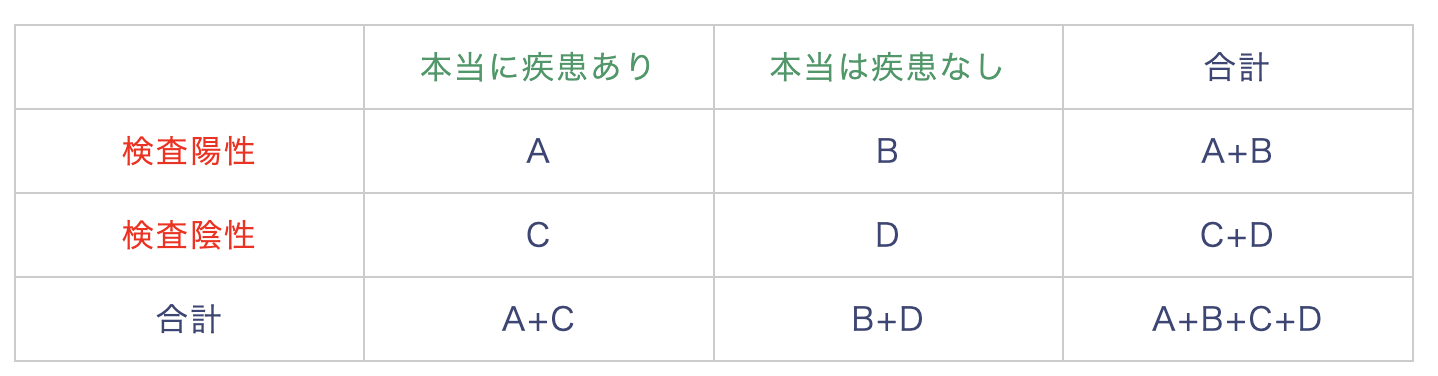
この時、感度と特異度の定義はこちらです。
感度の定義：A/(A+C)
特異度の定義：D/(B+D)
つまり、感度と特異度は日本語でいうと、以下の通りに言い換えることができます。
- 感度：疾患ありの人の中で、どれだけの人が検査陽性になるか。
- 特異度：疾患なしの人の中で、どれだけの人が検査陰性になるか。
この時にさらに感度を解釈していくと、感度とは「疾患がある人がこのぐらいいる」という結果が得られた条件のもとで検査陽性の人の割合（パラメータ）はどのぐらいか？を考えているということになります。
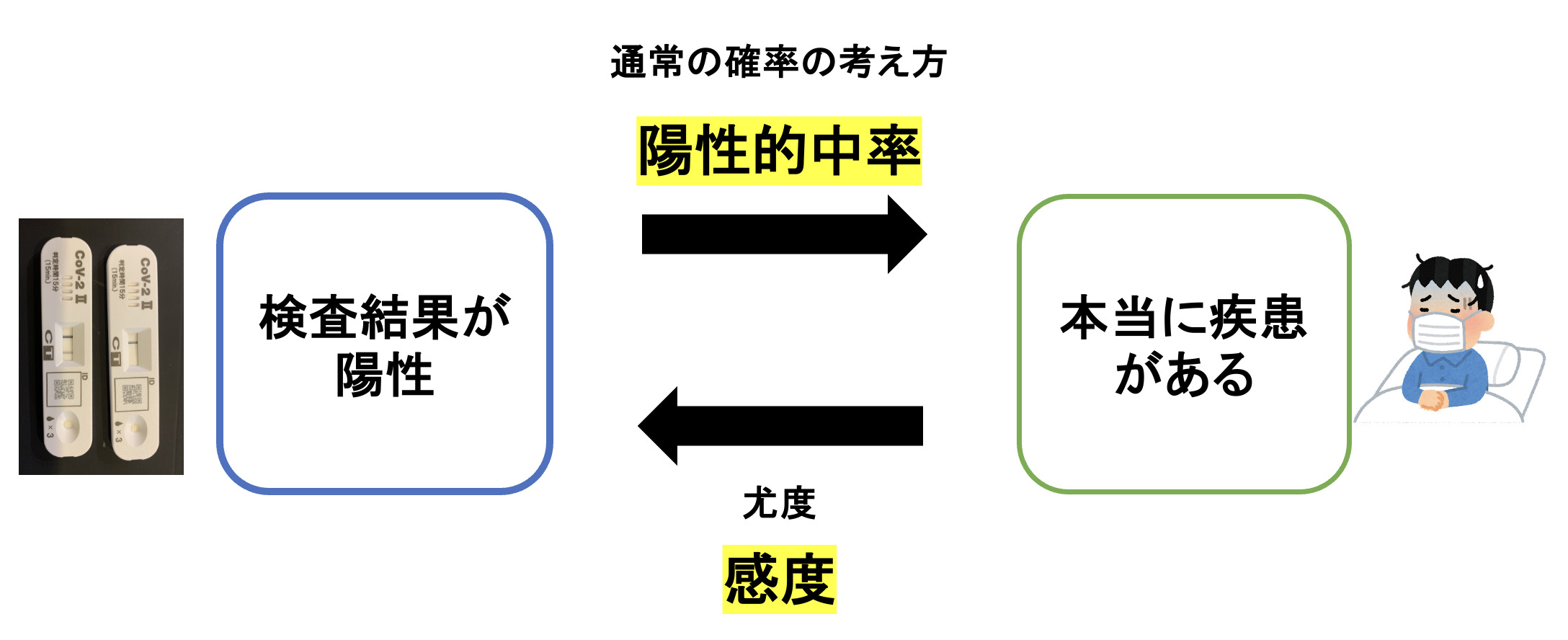
つまり感度は、「ある結果（や観測データ）」が得られた時にその結果を生み出す元となるパラメータはどれぐらいだろうか？ということの尤もらしさ、という尤度の定義に当てはまっているのです。
特異度に関しても同じで、「疾患のない人がこのぐらいいる」という結果が得られた条件のもとで検査陰性の人の割合（パラメータ）はどのぐらいか？を考えているから、尤度になります。
陽性尤度比と陰性尤度比は何を意味する？
「尤度とは何か？」「感度と特異度は尤度である」ということが整理できたところで、陽性尤度比と陰性尤度比の説明ができます。
「尤度比」はそのまま「尤度」の「比」です。
つまり、感度と特異度の比、ということ。
では陽性尤度比と陰性尤度比はどのような定義になるかといえば、下記のような数式で表されます。
陽性尤度比：（感度）/（1-特異度）
陰性尤度比：（1-感度）/（特異度）
陽性尤度比を日本語で言い換えると、「検査陽性となる尤度比」です。
感度は真に病気の人が検査陽性（真陽性）である尤度、1-特異度は病気でない人が検査陽性（偽陽性）である尤度、と言い換えることができるため、陽性尤度比は「病気でない人に比べて、病気の人は何倍検査陽性になりやすいか？」を示しています。
同様に陰性尤度比を日本語で言い換えると、「検査陰性となる尤度比」です。
1-感度は真に病気の人が検査陰性（偽陰性）である尤度、特異度は病気でない人が検査陰性（真陰性）である尤度と言い換えることができるため、陰性尤度比は「病気でない人に比べて、病気の人は何倍検査陰性になりやすいか？」を示しています。
陽性尤度比と陰性尤度比の使い方の例
陽性尤度比と陰性尤度比がわかったところで、実際にどう使うか？を解説します。
陽性尤度比と陰性尤度比を使うために重要な知識は、ベイズの定理です。
ベイズの定理そのものを詳しく理解するというより、下記の数式だけ覚えていただければOK。
事前オッズ×尤度比＝事後オッズ
これだけです。
この数式が何をいっているのかというと、
- ある事前の情報（事前オッズ）があった時に
- 検査をして尤度比を求める
- 事前オッズと尤度比をもとに、その情報のアップデートをする（事後オッズを計算する）
ということです。
ちょっと分かりにくいので、例を元にして考えてみます。
例で陽性尤度比と陰性尤度比の使い方を理解する
例えば、「冬に咳と鼻水を訴えてきた患者さん」がいたとします。
この時、以下のような流れを考えると、それぞれが「事前オッズ」「尤度比」「事後オッズ」に対応することになります。
- 「冬に咳と鼻水を訴えた場合」にインフルエンザである確率は50%ぐらいである、という感覚をお医者さんが持っていたとします。（事前オッズ）
- じゃあ本当にインフルエンザなのか？を診断するために、インフルエンザの検査をします。（この検査の尤度比は事前に知っている）
- インフルエンザ検査の結果、陽性だったので、この患者さんがインフルエンザである確率は97%だな、と判断する。（上記2つの情報から事後オッズの計算）
上記の例での実際に計算してみましょう。
- 事前情報でインフルエンザである確率は50%なので、オッズに直すと0.5/0.5=1。つまり、事前オッズは1
- インフルエンザ検査キット感度：60%、特異度98%である。そのため、陽性尤度比は0.6/(1-0.98)=30である。
- 事後オッズ（検査後のオッズ）を計算すると、1*30=30。オッズを確率に直すと30/(1+30)=96.8%のため、この患者がインフルエンザである確率は97%ぐらいだと診断する。
最後のオッズから確率計算は、オッズの定義：p/(1-p)を元に計算します。
と計算できます。
なお、インフルエンザ検査キット感度：60%、特異度98%という情報はこちらの記事から参考に引用させていただきました。
（引用：https://www.igaku-shoin.co.jp/paper/archive/y2019/PA03350_04）
まとめ
いかがでしたか？
この記事では「陽性尤度比と陰性尤度比とは？感度特異度との関係と使い方まで例を交えて解説」ということでお伝えしました。
- 陽性尤度比と陰性尤度比の基となる「尤度」とはそもそも何？
- 陽性尤度比と陰性尤度比は何を意味する？
- 陽性尤度比と陰性尤度比の使い方
が理解できるようになったのなら幸いです。
第1章：臨床研究ではなぜ統計が必要なのか？計画することの重要性
第2章：研究目的をどれだけ明確にできるのかが重要
第3章：p値で結果が左右される時代は終わりました
第4章：多くの人が統計を苦手にする理由
第5章：統計を使えるようになるために今日から何をすれば良いか？
第6章：統計を学ぶために重要な環境
もしあなたがこれまでに、何とか統計をマスターしようと散々苦労し、何冊もの統計の本を読み、セミナーに参加してみたのに、それでも統計が苦手なら…
私からプレゼントする内容は、あなたがずっと待ちわびていたものです。
