皆さんは「残差」という言葉を見たことがあるでしょうか。
回帰分析における残差平方和やカイ2乗検定の事後検定としての残差分析といったところで登場します。
また、残差と似た概念として「誤差」という言葉もよく出てきます。
残差や誤差は推測統計の根底を支える重要な概念ですが、統計ソフトウェアの出力には登場するものの学会発表スライドや論文にはそうそう登場しませんのでそれらの意味するところを知らない人も多いかもしれません。
この「残差」について、「誤差」との違いを踏まえつつ解説していきます!
残差とは何か?残差の求め方は?

残差とは、文字通り、残った差ということですが、何が残っているのでしょうか。
例えば、ある介入を行った5人と行わなかった5人について検査をした結果が下記の通りだったとします。

この介入に効果はないと考えるならば、各被験者の検査値は全員の検査値の平均値である26からバラついているだけと見ることになります。
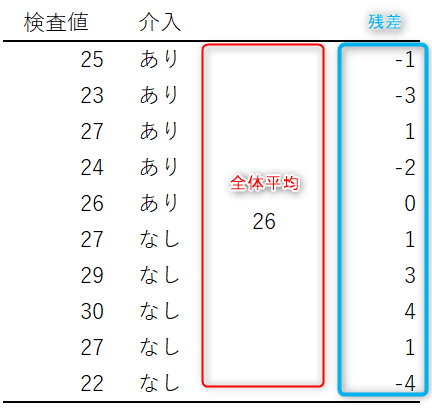
1番目の被験者の検査値は全員の平均値である26から1小さい25ですので、残差は-1となります。
では逆に、この介入には効果があると考えるとどうなるでしょう。
介入ありの5人の検査値の平均値は25、介入なしの5人の検査値の平均値は27ですので、残差は以下の通りになります。
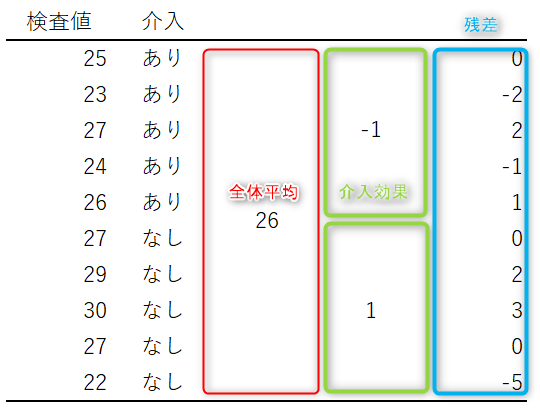
1番目の被験者の検査値は全員の平均値である26から介入の効果により1減った25ですので、残差は0となります。
また、10番目の被験者は全員の平均値である26から介入がないことにより1増えた27から5小さい22ですので、残差は-5となります。
このように残差とは、分析によって推定したモデルと観測された各データとのズレであり、推定したモデルによって説明できずに残った差のことです。
回帰分析の場合の残差とは?
残差は推定したモデルによって説明できずに残った差ですので、目的変数は説明変数と直線的な関係にあると考える回帰分析においては、回帰直線と各観測データとの垂直方向のズレが残差となります。
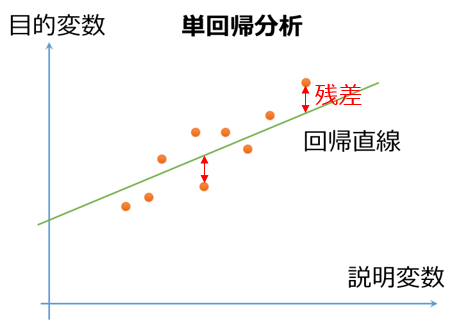
ちなみに、回帰分析で得られた偏回帰係数を用い、回帰式に準じて計算された値のことを予測値と呼びます。
誤差と残差の違いは?
残差が推定したモデルと観測された各データとのズレであるとして、それにいったいどのような使いみちがあるのでしょうか。
そのことを理解するためには、残差と似ているがまったくの別物である「誤差」についても知っておく必要があります。
誤差とは、真の値と観測された各データとのズレのこと。
真の値というのは、統計分析を用いて推定しようとしている対象集団(母集団)の値のことです。
上の例で言うと、(無限に存在するであろう)すべての対象者の検査値の平均値や、目的変数と説明変数の回帰直線(母回帰直線)による理論値のことです。
真の値は推定の対象なので、実際にいくつなのかは不明です。
したがって、観測された各データのもつ誤差もいくつなのかは不明です。
そこで、誤差が全体としてどのような性質をもつのかという観点で考えます。
2種類の誤差:系統誤差と偶然誤差
推測統計では、誤差には2種類あると考えます。
そのひとつは「系統誤差」です。
上の例で、介入に効果があることが真実だとすると、介入を受けた被験者をサンプリングすると小さめの検査値が観測され、介入を受けていない被験者がサンプリングされると大きめの検査値が観測されるはずです。
このように、一定の要因(この場合は介入の有無)によって生じる一方向へのズレを、系統誤差と呼びます。
系統誤差は分析において推定モデルに取り込むことができます。
介入の有無によって2群に分けるとか、説明変数を投入するとかいう作業は、系統誤差を取り込んでいることに他なりません。
もうひとつは「偶然誤差」です。
偶然誤差は文字通りたまたま生じた誤差のこと。
例えば、検査を受けた日がたまたま高かったというような、特定できない小さな要因(多くの場合は個人差という言葉で表現される)が、それぞれ無関係に影響して生じるランダムなズレのことです。
偶然誤差の性質
偶然誤差は、特定できない小さな要因によりランダムに生じることから、以下のような性質があります。
- 絶対値の小さい誤差は、絶対値の大きい誤差よりも多く起こる。
- 絶対値の同じ正負の誤差は、同じ確率で起こる
- 絶対値の非常に大きな誤差の発生する確率は非常に小さい。
この3つの性質を満たすように偶然誤差の分布を考えると、下記ようなかたちになりそうだと想像できますか。
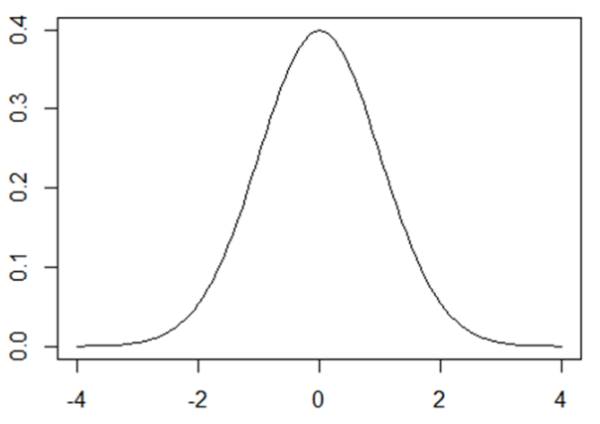
そうです。これは正規分布です。
正規分布というのは偶然誤差を表現する確率分布と言うこともできます。
回帰分析などで残差が正規分布に近いか否かということはどんなことを意味する?
特定の要因によるズレを取り除くと、偶然誤差のみになり、その分布は正規分布となります。
ということは、介入に効果があるのが真実であれば被験者全体の平均値からの残差には系統誤差が残っているので、介入の有無によって特徴的な誤差のかたまりが2つできそうです。
そして、介入の有無によって2群に分けて各群の平均値からの残差を求めると、系統誤差の多くは取り除かれるためその分布は正規分布に近づくはずです。
残差が正規分布に近いと良いこと
推定したモデルによって求められた残差の分布が正規分布に近いと、推定したモデルによって系統誤差が取り除かれたと考えることができます。
それは、推定したモデルに用いられている、群分けや説明変数で観測値が説明できていることに他なりません。
推定したモデルが正しい可能性があるとみることができます。
また、t検定をはじめとしたパラメトリックな検定や線形回帰分析は、誤差項に正規分布を仮定しています。
これは、残差には偶然誤差の部分しかないと考えていることですので、残差が正規分布に近いことにより、分析することの妥当性が担保されます。
残差の正規性に関するシミュレーション
実際にシミュレーションしてみましょう。
介入の効果があるのが真実であるとして以下を仮定します。
- 介入を受けると検査値の平均値が24
- 介入を受けないと検査値の平均値が28
- 標準偏差は両群ともに1
この時、介入を受けた群が200人、介入を受けていない群が800人、合計1000人をランダムサンプリングすると以下のようなヒストグラムになります。

介入を受けていない群のほうが多いので、28付近に多くの被験者が存在していますね。
この1000人の被験者について、全体平均との残差を図示すると以下のようになります。
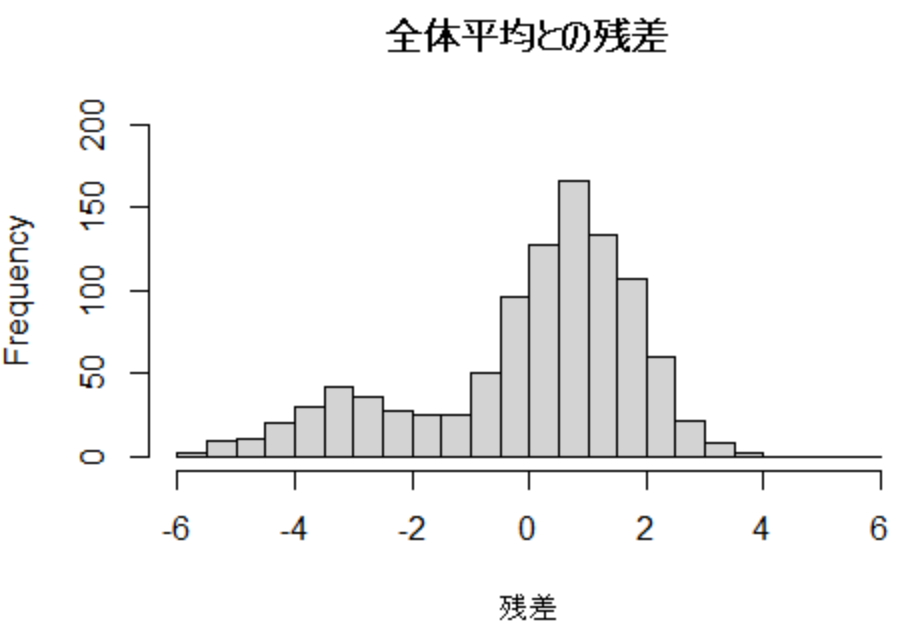
正負それぞれに山があり、系統誤差が疑われます。
では、各群の平均との残差を図示すると下記のような形になります。
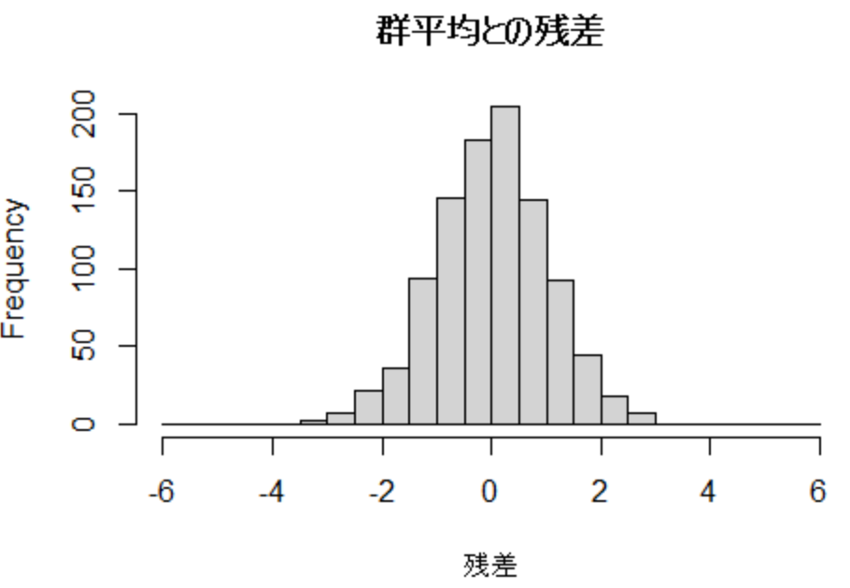
2つの山が1つになり、全体平均との残差に比べると正規分布に近づいているのがわかりますね。
このように、残差の分布から母集団の状況が推測できるわけです。
まとめ
残差という概念は、自らが推定しているモデルと観測値との差のことですが、母集団における誤差という概念と密接に関係しています。
推測統計の多くの手法は、残差の状況をもとにして推測していると言っても過言ではありません。
パラメトリックな検定や回帰系の分析は残差の正規性を仮定していますが、残差が正規分布に近いということは設定しているモデルが妥当であることの根拠になります。
残差の概念を理解するとともに残差の分布に気をつけることで、より精緻な分析を行うことができます。













コメント