重回帰分析やロジスティック回帰分析には”最尤法”や”最小二乗法”といった手法があります。
これらは一体どんな手法で何が違うのか、疑問に思っている方も多いのではないでしょうか。
本記事は最尤法や最小二乗法について、なるべくわかりやすく解説します。
初心者の方でも大丈夫なように、難しい計算式は極力使わずに説明しますので安心して下さいね。
回帰分析を実施する上で最尤法などは避けて通れない概念ですので、意味だけでも是非覚えていってくださいね!
最尤法(最尤推定)と最小二乗法とは?

まずは、最尤法と最小二乗法の違いから確認していきましょう!
最尤法と最小二乗法の違い
あるサンプルデータの平均値をそれぞれの手法で計算するとしましょう。
この時、以下の方法でそれぞれ平均値を求めようとします。
- 最尤法:サンプルデータが得られる確率(尤度)が最大になる平均値を探す
- 最小二乗法:サンプルデータとの誤差が最小になる平均値を探す
最尤法では確率に注目して解析する点が最大の特徴です。
最尤法ではこの確率のことを、尤度(もっともらしさ)と表現し、尤度を最大にすると表現します。
最尤法は解釈が難しいので、後ほど詳しく説明しますね。
まずは解釈が簡単な最小二乗法の説明からしていきましょう。
最小二乗法はどんなことをしている?
先ほどの例を使って最小二乗法の中身について解説していきます。
サンプルデータを{2,4,6}の3つの値だとしましょう。
平均値はまだ不明なため、xとおきます。
最小二乗法は、xとサンプルデータの各誤差を二乗して足し合わせた値が最小となるxを探します。
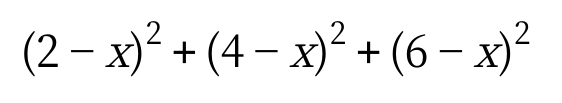
この式が一番小さくなるxの値を平均値として判定します。
これがいわゆる最小二乗平均、と呼ばれる平均値。
今回の例ではx=4の時に最小になったため、4を平均値として判定します。
最尤法はどんなことをしている?
ではいよいよ最尤法です。
最尤法では母集団が正規分布に従うことを仮定します。
“母集団が正規分布に従うとした場合、平均値がいくつの時が一番{2,4,6}のサンプルデータが得られやすいか?”
最尤法ではこのように考えて計算していきます。
サンプルデータが出る確率=(2が出る確率)×(4が出る確率)×(6が出る確率)
x=2,3,4の場合それぞれ確率を算出していきます(値は適当です)。
x=2の時 → 2が出る確率=0.5,4が出る確率=0.05,6が出る確率=0.0001
x=3の時 → 2が出る確率=0.2,4が出る確率=0.2,6が出る確率=0.001
x=4の時 → 2が出る確率=0.05,4が出る確率=0.5,6が出る確率=0.05
それぞれの確率を掛け合わせると、(2,4,6)のサンプルデータが得られる確率が算出できます。
最尤法では、これらの確率が最大となるxの値をこのデータの平均値として判定します。
今回の例ではx=4の時に確率が最大になったため、このデータの平均値は4として判定します。
以上が最尤法の計算の流れです。
ちょっと難しいかもしれませんが、最尤法は”確率”に注目して計算していることだけでもおさえておいて下さい!
また、今回は最小二乗法も最尤法も同じ平均値になりました。
どちらの手法も基本的に大きな差が出ることはなく、平均値のようなシンプルなものだと同じ値になる傾向があります。
最尤法において対数尤度を最大化するとは?

最尤法を勉強していくと「対数尤度を最大にする」ということをよく目にします。
では「対数尤度を最大にする」ということはどういうことか、確認していきましょう!
対数尤度関数とは?
最尤法は”対数尤度関数が最大になる値”を算出します。
この対数尤度関数とは何でしょうか?
対数尤度関数は尤度関数を対数変換したものなのですが、この”尤度関数”とは何かご説明しましょう。
ここでも先ほどの平均値を求める例を使って説明していきましょう。
サンプルデータが出る確率=(2が出る確率)×(4が出る確率)×(6が出る確率)
先ほどの例ではサンプルデータが出る確率をこのように表現しました。
これが”尤度関数”です。
もう少し詳しく説明すると
“尤度関数=各パラメータが出る確率を掛け合せたもの”
ということです。
ちなみに計算式はこんな感じです。
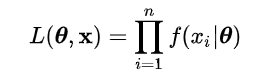
θ=確率分布(今回は正規分布を仮定したので、正規分布の平均値と分散がθになります)
x=求めたい値(今回の場合データの平均値)
初見だと訳がわからないと思いますが、安心して下さい。
要するに「仮定した正規分布から各データが得られる確率を算出して全部かけました!」と言っているだけです。
対数尤度関数を最大にする理由
例では尤度関数が最大になるxの値をデータの平均値だと判定しました。
尤度関数を最大になるxの値は、真の平均値である確率が最も高い値だからです。
さらに噛み砕くと、結果が正しい確率が最も高い値だからです。
もちろん計算結果はなるべく正しくあってほしいところですので、尤度関数がなるべく高い値を選びたいですよね。
これが対数尤度関数を最大にする理由です。
ここまで理解できると
「尤度関数のことはなんとなく分かった。でも対数変換しているのはなぜ?」
といった疑問をもたれると思います。
なぜ対数変換するのか説明しますね。
なぜ対数に変換するのか?
尤度関数を対数変換する理由は、”計算上都合がいいから”です。
先ほど説明したように、尤度関数は掛け算の形になっています。
最大値を求める計算では微分を使うのですが、掛け算の形だと微分がしにくいんですよね。
ですので、以下のように対数変換して掛け算を足し算の形に変えることで微分しやすくしているだけです。
A×B→log(A×B)=log(A)+log(B)
log内の掛け算はこのように足し算に変換できるので、足し算になってしまえば微分は簡単、というわけです。
以上の理由から、最大値を計算するために尤度関数を対数尤度関数に変換してから計算しているというわけです。
対数尤度の近似とWald信頼区間
実は、この対数尤度とWald信頼区間と呼ばれる信頼区間は、とても相性がいいのです。
かなり一般的な状況で、パラメータθの対数尤度関数は、最尤推定量\(\hat{θ}\) を頂点とする二次関数で近似できるのです。
この性質は、信頼区間を求めるために便利な性質で、この信頼区間の構成方法をWald(ワルド)方という。
二次関数のため、当然のことですが、Wald信頼区間の上限と下限は\(\hat{theta}\) の上下対象になります。
例えば、パラメータが1個で、その標準誤差をSEと表すと、95%Wald信頼区間は
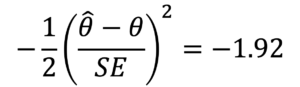
を解くことで求められる。すなわち、
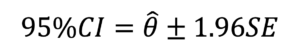
である。
この信頼区間は、サンプルサイズが大きくなれば近似精度が高くなり、計算上の誤差は小さくなる。逆に言えば、サンプルサイズが小さければ、誤差が無視できない時もある。
最尤法での推定をロジスティック回帰を例に

それでは、先ほどまで解説した最尤法を、ロジスティック回帰分析を例にしてみていきましょう。
ロジスティック回帰とは
ロジスティック回帰とは、たくさんの変数を使って2値の分類をする関数を作る手法です。
医療統計では”自宅退院の有無に関わる変数を見つけたい”といった場合に使われます。
ロジスティック回帰では基本的に最尤法を使って偏回帰係数などのパラメータの算出を行います。
ここではロジスティック回帰で最尤法がどのように行われているのか解説していきます。
ロジスティック回帰について詳しく知りたい方はこちらの記事をご覧ください。
ロジスティック回帰の尤度関数
ロジスティック回帰で尤度関数は以下のように表します。
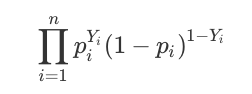
ロジスティック回帰は目的変数が2値です(ここでは「0」と「1」の2値だとしましょう)。
目的変数が「1」になる確率をpとすると、「0」になる確率は(1-p)となります。
これらの値をデータの数だけ全て掛け算したものが、上記の尤度関数です。
ロジスティック回帰では、この尤度関数が最大になる各偏回帰係数を算出していくわけです。
ロジスティック回帰の実際
ロジスティック回帰はSPSSやEZRなどの専用ソフトを使うことで解析できます。
どのソフトも特に指定しなければ基本的に最尤法を使って解析を実行します。
分析のかけ方や結果の解釈は以下の記事で解説していますので、是非ご覧ください。
まとめ

最後におさらいをしましょう。
- 最小二乗法はサンプルデータとの誤差が最小になる値を算出する
- 最尤法はサンプルデータが得られる確率が最も高い値を算出する
- 最尤法は対数尤度関数が最大となる値を求めることで値を算出する
- ロジスティック回帰では基本的に最尤法を使ってパラメータを推定している
最尤法は計算式が難しいため難解な方法だと思われがちです。
ですがここまでで説明したように、最尤法は”確率”を計算しているだけだと理解してしまえば案外解釈しやすいものです。
最尤法はよく登場する言葉ですので、是非理解していってくださいね。
最後までお読みいただきありがとうございました。













コメント
コメント一覧 (1件)
[…] ロジスティック回帰分析など多くの多変量解析では最尤法を用いて推定しています。 […]