今日の記事は、統計解析ソフトJMPでマンホイットニーのU検定を実施する方法をお伝えします。
マンホイットニーのU検定はどんな検定だったか覚えていますか?
ウィルコクソンの順位和検定とやっていることは同じで、連続量を対象としたノンパラメトリック検定ですよね。
では、連続量を対象としたパラメトリック検定は?
そう、T検定です。
ということで、今回の記事はマンホイットニーのU検定をJMPで実施する方法に加えて、同じデータに対してT検定を実施した時の違いまで解説します。
JMPでマンホイットニーのU検定(Wilcoxonの順位和検定)を実施するために必要となるデータを読み込む

まずは、マンホイットニーのU検定(以下、U検定)を実施するために必要なデータを解説します。
U検定は、2群の連続量を対象としたノンパラメトリック検定でした。
ということは、用意するデータは以下の2つを満たす必要があります。
- 連続量のデータが必要。
- 2群の群間比較をするので、2つのカテゴリを持つ、カテゴリカルデータが必要。
JMPでマンホイットニーのU検定を実施するのに使用するデータ
ということで、今回の記事で使うデータです。
今回はJMPにあるサンプルデータの中から「Lipid data」を使います。
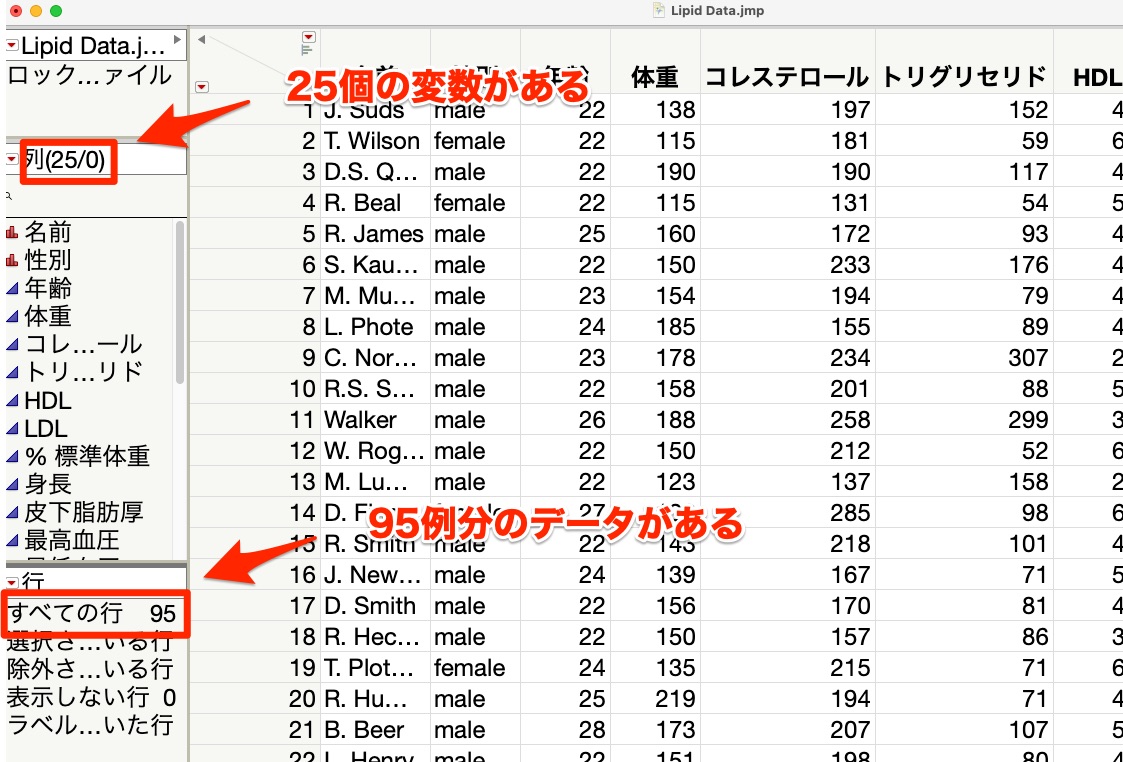
Lipid dataは以下のようなデータになっていて、25個の変数が95例分あることがわかります。
今回はこのデータから「性別間でトリグリセリドの分布に違いがあるのか」をマンホイットニーのU検定で確認していきます。
JMPでマンホイットニーのU検定を実践する!
では早速、JMPでマンホイットニーのU検定を実施してみましょう。
U検定を実施するには、以下の手順で行います。
「分析」→「二変量の関係」
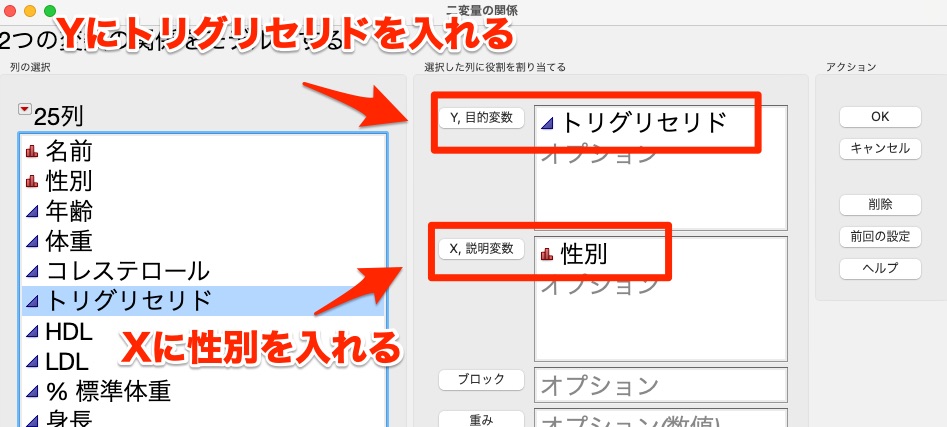
その後、以下の操作をします。
- Y,目的変数にトリグリセリドを入れます。
- X,説明変数に性別を入れます。
- 他は、いじらなくてOKです。
すると下記のように性別ごとにトリグリセリドの値がプロットされます。
この画面の左上の赤い三角形のボタンを押します。
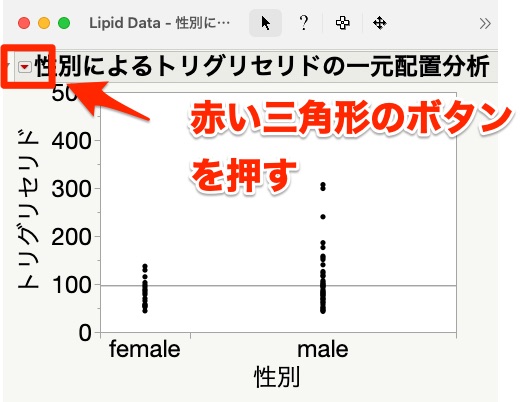
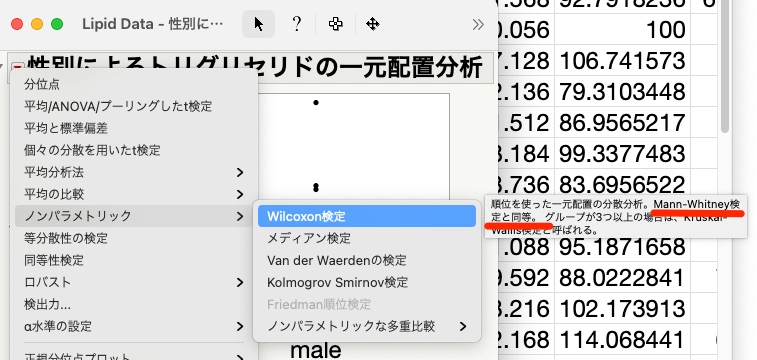
すると以下のような画面になるので、「ノンパラメトリック」→「Wilcoxon検定」を押します。
マンホイットニーのU検定じゃないじゃないか!と思うかもしれませんが、右側の説明にも書かれてある通り、Wilcoxonの順位和検定はマンホイットニーのU検定と同等ですので、Wilcoxon検定を選択することでOKです。
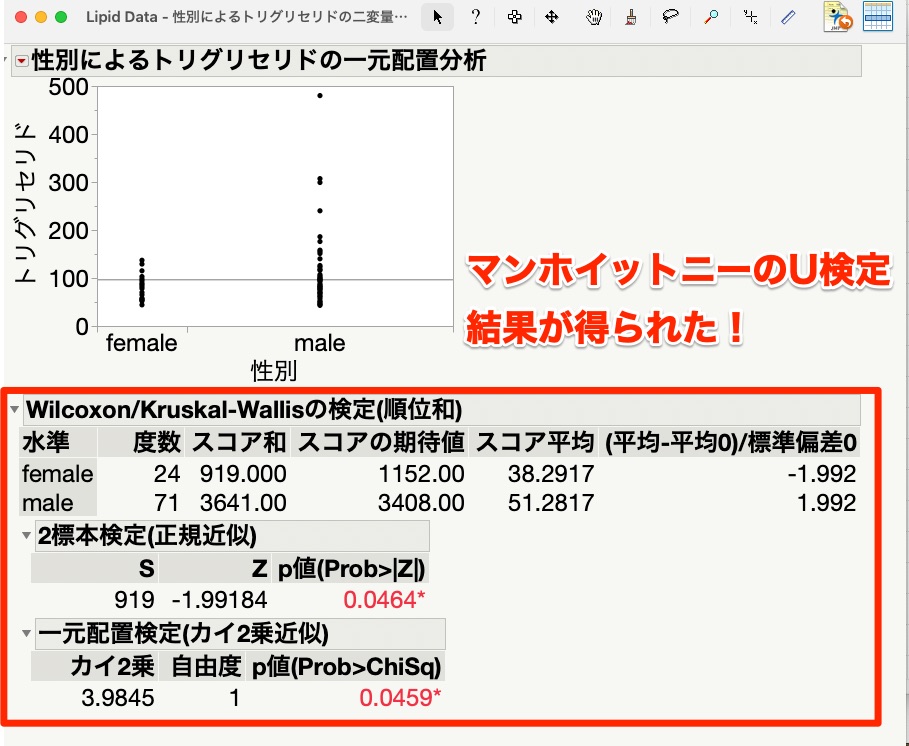
すると、グラフの下にマンホイットニーのU検定(ウィルコクソンの順位和検定)の結果が表示されました。
JMPで出力したマンホイットニーのU検定結果の解釈をしよう
実際にU検定が実施できました。
では、結果の解釈をしていきましょう。
マンホイットニーのU検定の結果解釈
JMPでウィルコクソンの順位和検定を実施すると、2つの検定結果が出てくることがわかります。
- 正規近似に基づく検定結果
- カイ二乗近似に基づく結果
の2つですね。(もう一度、先程の結果の図を掲載します)

正規近似およびカイ2乗近似の検定は、いずれも検定統計量の漸近分布に基づいたものです。
2つの検定結果には大きな差がありませんが、どちらの結果を使うのかを事前に決めておくことが大切です。
どちらの結果を採用するにしてもP値は0.05を下回っているため、今回の結果は「有意差あり」です。
つまり、「今回のデータでの男性のトリグリセリドと女性のトリグリセリドは異なる」という結論になります。
同じデータでT検定を実施すると、マンホイットニーのU検定結果とどう違うのか?
以上の手順で、マンホイットニーのU検定をJMPで実施することができました。
次なる疑問は、同じデータでT検定を実施すると結果はどうなるのか!?ということ。
気になりますよね。
では実際に調べてみましょう。
JMPでT検定を実施する詳細な手順は、こちらの記事から確認してみてください。
同じデータに対してStudentのT検定を実施した結果が以下です。
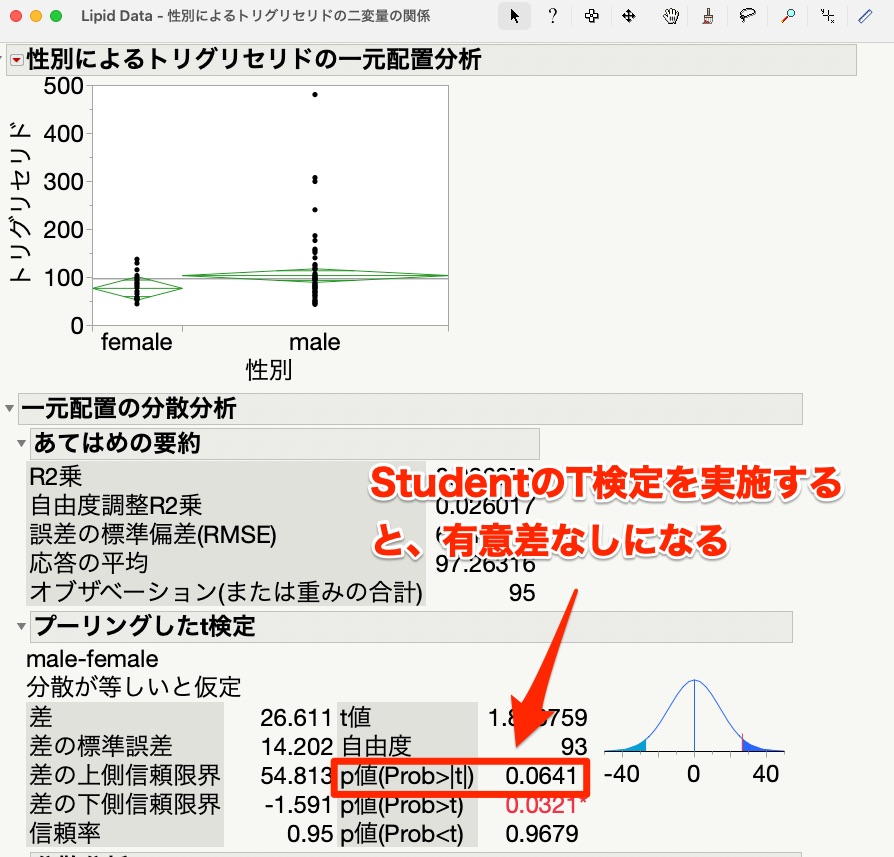
両側検定でp=0.0641ですので、有意差なしという結果ですね。
つまり、T検定の結果の方が、P値が大きいことが分かります。
T検定とU検定の検定結果の違いはこのような関係になります。
| データの分布 | T検定(パラメトリック) | ウィルコクソンの順位和検定(ノンパラメトリック) |
| 正規分布 | ◎ | ◯ |
| 正規分布ではない | × | ◯ |
今回のデータは正規分布といえない分布だったことが考察ができます。
性別ごとのプロットを見てもわかる通り、maleには値が大きい方に外れ値があり、正規分布とは言えない可能性があることがわかります。
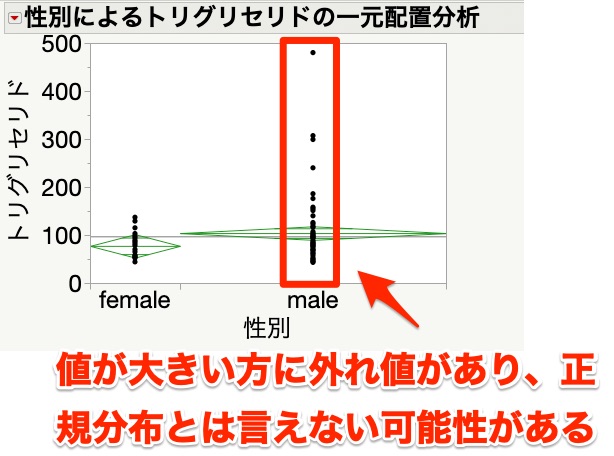
正規分布の判断は難しいところですが、間違っても正規性の検定はしないようにしましょう。
p値はデータの数によって大小が変わる性質があり、正規性の判断としては使いにくいためです。
ヒストグラムやQQプロットを確認し、先行研究で正規分布として扱われているかどうかを確認することの方が、とても有益です。
JMPでマンホイットニーのU検定まとめ

今回は、JMPでマンホイットニーのU検定を実施しました。
同じデータでT検定を実施すると、今回のデータではT検定のP値の方が大きくなっています。
データの分布を確認するとデータが正規分布とは言えない形をしていたため、この結果には納得です。












コメント