この記事では「EZRでウィルコクソンの符号付順位和検定を実施!対応のあるノンパラ手法」としてお伝えします。
対応のある連続データに対するノンパラメトリックな検定手法は、ウィルコクソンの符号付順位和検定Wilcoxon signed rank test(1標本Wilcoxon検定とも呼ばれます)があります。
この記事では統計ソフトEZRを使ってWilcoxonの符号付順位検定の実施方法と分析結果の解釈を行います。
ウィルコクソンの符号付順位検定(Wilcoxon signed rank test)とは?

ウィルコクソンの符号付順位和検定(Wilcoxon signed rank test)は、対応のあるt検定のノンパラメトリック版です。
ウィルコクソンの符号付順位和検定がどんな時に使えるか、という適用条件をまずは整理しましょう。
- 連続量のデータであること
- 1つの標本に対して条件を変えて得た2つのデータであること(対応のあるデータであること)
ノンパラメトリックなので、条件が少ないですね。
ウィルコクソンの符号付順位和検定での仮説は、変数Aと変数Bを比較するとすれば、
帰無仮説H₀:Aの分布中心=Bの分布中心
対立仮説H₁:Aの分布中心≠Bの分布中心
という仮説を立てて、検定します。
EZRでウィルコクソンの符号付順位和検定を実施する

ウィルコクソンの符号付順位和検定を整理できたところで、EZRで実際に実施していきましょう!
使用するデータは架空のデータで、20人に対してBeforeとAfterのデータが取得できている状況。
このようなデータですね。
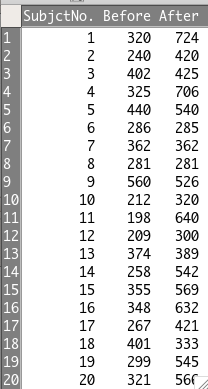
対応のある検定を実施したいときには、比較したいデータを別の列に保持しておくことが重要です。
今回のデータでも「Before」の列と「After」の列で別になっていますよね。
データクリーニングの基本である「1症例1行のデータにする」ということが守られていればOK。
箱ひげ図を作成してみると、これだけ違いのある状況のデータです。
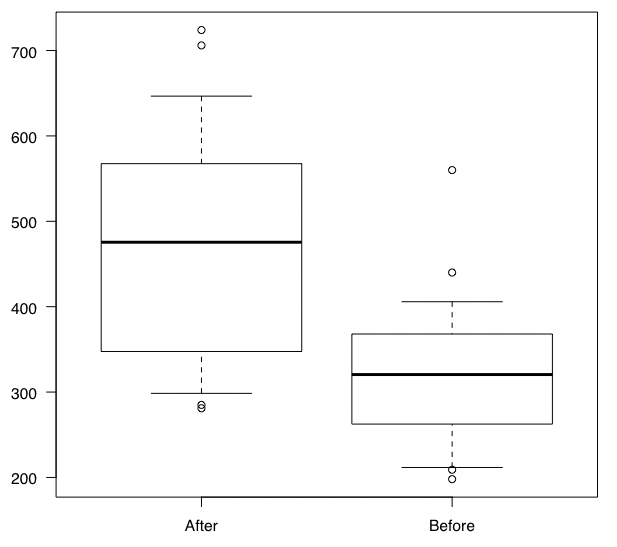
このデータに対して、ウィルコクソンの符号付順位和検定を実施していきましょう。
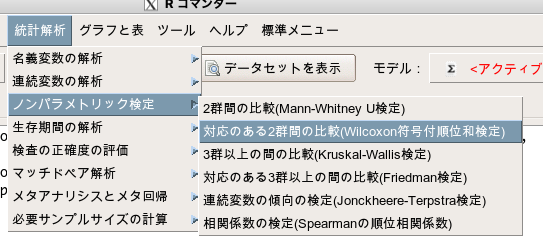
まずメニューから[統計解析]→[ノンパラメトリック検定]→[対応のある2群間の比較(Wilcoxon符号付順位和検定)]を選びます。
次に、下記のダイアログボックスが現れるので、[第1の変数]にBeforeを、[第2の変数]にAfterを選択します。
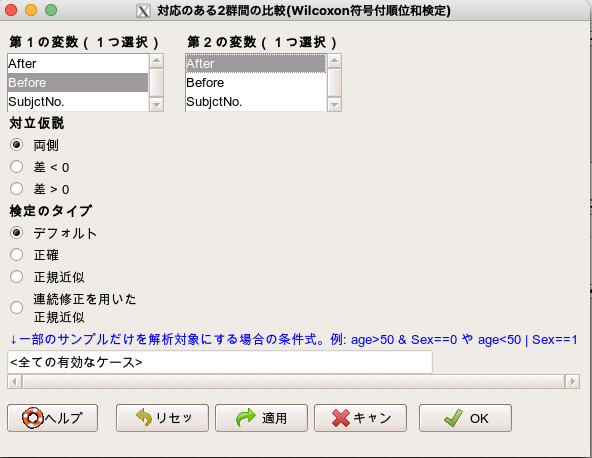
そしてOKを押すだけ。
そうすると、ウィルコクソンの符号付順位和検定の結果が出力されます。

SPSSによるWilcoxonの符号付順位検定の結果の読み方
再度、結果を掲載します。

ここで注目すべき点は有意確率(P値)です。
この有意確率(P値)が事前に設定した有意水準(0.05や0.01)未満だと有意に差ありということになります。
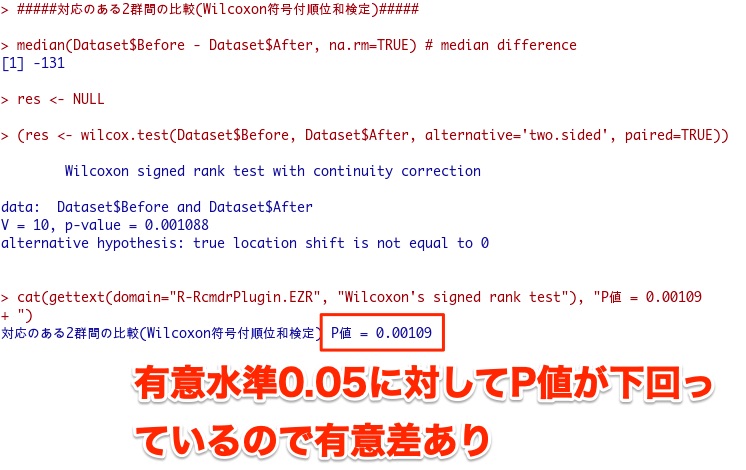
ここではp=0.00109であり、有意水準0.05に対して有意な差が見出された、ということになります。
ノンパラメトリックな手法の基本的な要約統計量
ノンパラメトリックな手法を行ったときの要約統計量は、中央値と四分位範囲を述べるべきだとされています。
医学論文では、ノンパラメトリックな手法を行っても平均と標準偏差を提示することが多いですが、データが正規分布に従っていないのであれば、平均と標準偏差の情報は役に立たないことを理解しておく必要があります。
まとめ

この記事ではEZRでウィルコクソンの符号付順位和検定を実施する方法をお伝えしました。
対応のあるノンパラメトリックな検定ということで、適用条件は以下の二つでしたね。
- 連続量のデータであること
- 1つの標本に対して条件を変えて得た2つのデータであること(対応のあるデータであること)
ぜひ結果の解釈までご自身でできるようになっていきましょう!













コメント