重回帰分析やロジスティック回帰分析などの多変量解析を用いて、
- 無数にあるリスク要因候補から影響を与えている要因を特定する探索的な研究
- 説明変数候補に対してサンプル数のバランスが悪い研究
- 多重共線性の疑われる複数の説明変数候補から最適な変数を選択
- 疾患の予後予測モデルを作成
といったことを行いたいとき、説明変数の組合せをどのように決定すべきなのか。
その問題に解答を与えてくれる指標の一つにAIC(赤池情報量規準)があります。
AICはその導出等の背景にあるものは難解ですが、意味合いをざっくりと捉えることはそう困難ではありません。
この記事では、AICについてわかりやすく解説していきますね!
AICが必要な場面:モデル選択時

重回帰分析やロジスティック回帰分析といった多変量解析を用いた研究において投入する説明変数の組合せ選択(モデル選択)を行う必要があるのは、例えば以下のような場合です。
- 説明変数候補が無数にある
- 説明変数候補とサンプル数のバランスが悪い
- 多重共線性を回避したい
- 予測モデルを作りたい
それぞれの場面について詳しくみていきましょう!
AICが必要な場面:説明変数候補が無数にある
EBMの考え方や電子カルテの普及によって、医療機関でも様々なデータが常時蓄積されるようになり、以前に比べると研究に必要なデータが容易に得られるようになりました。
これは研究をする上で大変喜ばしいことなのですが今までは取得できなかったデータが存在することで多変量解析に投入可能な説明変数の種類が多くなりすぎて困ることもあります。
(場合によっては何百もの候補もあり得ます…)
本来的には、研究仮説に基づいて、説明変数候補を選択するわけですが、探索的にどの説明変数がリスク要因になっているか分析したいことも多くあります。
このような場合には、AICが活躍することがあります。
AICが必要な場面:説明変数候補とサンプル数のバランスが悪い
上記の通り、取得できるデータの種類は増えてきましたが、稀少疾患に関するケースや単施設の被験者を対象としたケースなどでは、サンプル数がそれほど多くはないという場合が存在しますね。
必要サンプル数は分析の種類や仮説次第で変化します。
例えば、重回帰分析においては、おおむね、説明変数の数の10倍以上のサンプル数が望ましいと言われております。
そうすると、限られたサンプル数に対して多すぎる説明変数候補があるという問題が発生します。
また、限られたサンプル数に対し、過度に多くの説明変数を投入してしまうと
そのサンプルに対してのみ適合してしまう(「オーバーフィッティング」という)という危険性もあります。
このような場合には、AICが活躍することがあります。
AICが必要な場面:多重共線性を回避したい
複数の説明変数間に強い関連性がある場合、それらの説明変数を同時に投入してしまうと、多重共線性を起こし、推定結果が疑わしいものとなってしまいます。
多重共線性の疑われる説明変数候補が多く存在する場合、最適な組合せを知る必要があります。
このような場合には、AICが活躍することがあります。
AICが必要な場面:予測モデルを作りたい
医療分野において多変量解析を行う場合、目的の一つとしてはリスク要因を見つけ出すことが目的かと思います。
しかし、慢性疾患やリハビリのように、長期にわたって対象者と関わるようなケースでは疾患の予後や治療の効果を予測するモデルを作成するという研究も散見されます。
この場合、予測の精度を向上させる説明変数の組合せを見つけるとともに臨床現場で使いやすいものにするためできるだけ少ない種類の説明変数で予測できることが望ましいです。
このような場合には、AICが活躍することがあります。
モデル選択にも有用なAICとはそもそもどんな指標?

上記のような適切な説明変数の組合せを選択する必要がある場合、その選択法の一つとして提案されたものがAIC(赤池情報量規準)です。
名前にある通り、日本の数理統計学者である赤池弘次先生が考案したものでモデル選択の標準的な手法として世界的に用いられているものです。
ロジスティック回帰分析など、医療統計でよく用いられる多変量解析におけるAICの計算式は以下の通り。
AIC=-2logL+2(k+1)
L:モデルの最大尤度、k:説明変数の数
AICが意味しているのはどんなこと?
AICの計算式には
- 最大尤度やlogが入っているし
- なぜか2倍しているし
という具合によく分かりませんよね。。
このAICを厳密に理解するためには情報理論で扱われるカルバック・ライブラー情報量などを知らなければなりません。
それは骨が折れますから、本質を失わないようにしつつもざっくりと理解していきましょう。
AICの大小と適切なモデルの関係
AICの式の第1項の中心は最大尤度です。
ロジスティック回帰分析など多くの多変量解析では最尤法を用いて推定しています。
最尤法は分析に使用しているサンプルの出現確率が最も高くなるような場合のパラメータを推定する方法ですが、その推定されたパラメータに基づくサンプルの出現確率が最大尤度であると考えて問題ありません。
サンプルの出現確率が高いほど推定されたモデルはサンプルに適合しているため、最大尤度が大きいほど良いモデルであると言えます。
最大尤度は確率と同じように0と1の間の値になるため、対数(log)で変換をして扱いやすいかたちにしています。
さらにマイナスを付けているので大小関係が反転します。
つまり、AICは小さければ小さいほど良いモデルということになります。
しかし、説明変数の数を増やすとデータにより適合するモデルを推定することができるため(オーバーフィッティング)、第2項では、説明変数の数を用いてペナルティをかけています。
説明変数の数を増やすと第1項の部分は小さくなりますが、第2項の部分は大きくなります。
この2つのバランスから、説明変数の数を増やすのに十分な尤度の上昇が得られているか。
という観点で規準化したものがAICです。
AICの値の解釈:相対的な評価しかできない
AICが小さいほど良いモデルです。
しかし、値そのものに意味はありません。
「いくつより小さければ良い」という絶対的な値があるわけではないため、複数のモデルを比較し、AICの小さい方がより良いモデルという相対的な評価をしていきます。
AICを使った説明変数選択・モデル選択の分析例
AICに関してざっくりと分かったところで、実際の分析例をみていきましょう!
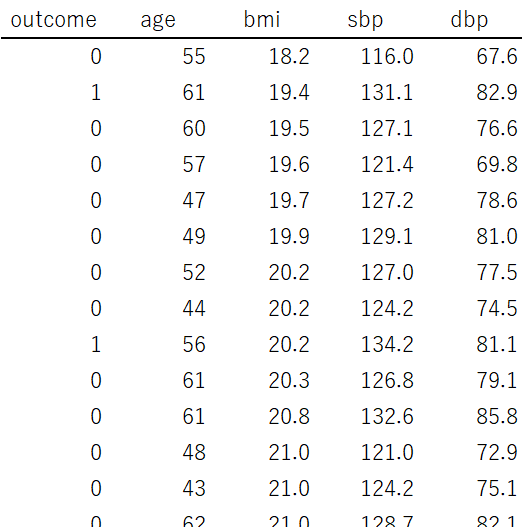
上記のようなデータであるアウトカムの発生に年齢、BMI、収縮期/拡張期血圧が寄与しているのではないかと考えてロジスティック回帰分析を行うとします。
このデータは60名の患者データで説明変数の候補が4つですのでややバランスの悪い状況です。
加えて、収縮期/拡張期血圧は相互に関連していることは明らかですから多重共線性も心配になります。
この2点からモデル選択の必要性があると考えられます。
このデータに対してすべての説明変数の組合せごとにロジスティック回帰分析を実施しAICの小さい順に並べたのが下の結果です。
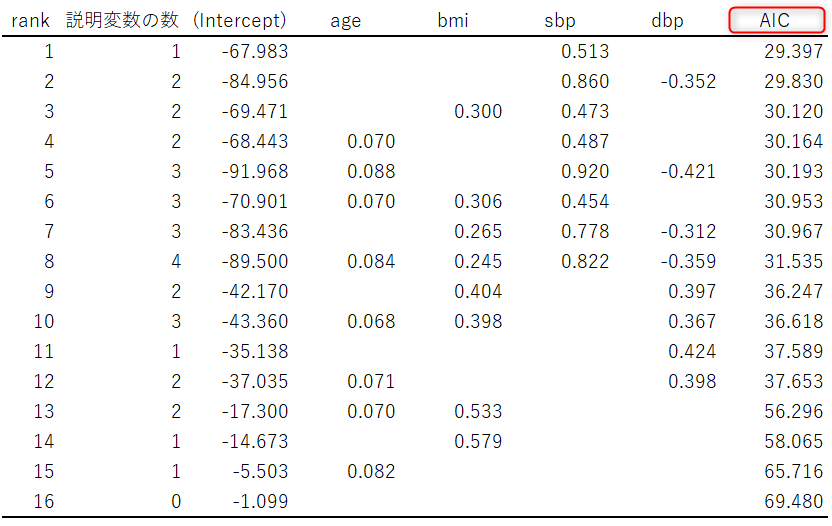
各説明変数にある値は推定値(オッズ比に変換する前の値)で、空欄になっているところはその説明変数が投入されていないモデルです。
AICが最も小さいのは、sbp(収縮期血圧)のみのモデルになります。
また、sbpとdbpの列に注目すると、dbpがsbpと一緒に説明変数となっている場合とdbp単独の場合とで、符号が変わっています。
このことから多重共線性が生じていることも示唆されます。
そこで、説明変数1つでは心許ないとすれば、sbpのつぎに加えるべきは、2つ目のモデルのdbpではなく3つ目のモデルのBMIということになります。
実際にロジスティック回帰を実施したい場合には、EZRやSPSS、JMPなどでやってみましょう。
AICが出てくるはずです。
まとめ
多変量解析を行う際、説明変数の組合せをどうしたら良いのか、という問題に出くわすことはよくあります。
説明変数の候補が多くなれば、仮設の設定も容易ではなく、オーバーフィッティングや多重共線性のことも気にしなければなりません。
そのようなときに、分析のヒントを与えてくれるのがAICです。
AICのより小さいモデルを探索することでより良い分析を行うことができます。
もっとも、AICも万能なものではなく、BIC(ベイズ情報量規準)など他の適合度指標も数多く提案されています。
研究で用いる際には、AICでモデルの目途をつけた上で、あらためて研究仮説を構築するということも大事になってきますね。
動画でもAICについて解説していますので、合わせてご参照くださいませ^^












コメント