この記事では統計ソフトSPSSを用いた多重ロジスティック回帰分析(多変量ロジスティック回帰分析)の実施方法と分析結果の解釈を行います。
多重ロジスティック回帰分析は多変量解析の一種で、重回帰分析の考え方と非常に似ています。
ですので、先に重回帰分析を理解しておいた方が、多重ロジスティック回帰分析をスムーズに理解できるかもしれません。
どうしても先に多重ロジスティック回帰分析を理解したいという方は、この記事の後でもいいので重回帰分析をしっかり理解して下さい。
それでは多重ロジスティック回帰分析について一緒に考えていきましょう!
多重ロジスティック回帰分析とは?
多重ロジスティック回帰分析(多変量ロジスティック回帰分析)は、最近医学研究で類繁に使われるようになった手法です。
重回帰分析の従属変数は連続変数(比率尺度、間隔尺度、段階数の多い順序尺度)です。
それに対して、多重ロジスティック回帰分析の従属変数は2値のカテゴリカルデータ(例:男性・女性、患者群・健常者群など)になります。
多重ロジスティック回帰分析の利点はデータの型や分布に、あまり厳密さを要さない点です。
多重ロジスティック回帰分析のメリット
重回帰分析は、データが間隔尺度または比率尺度でなければ適用できません。
また重回帰分析は、残差が正規分布に従うという仮定の下で理論的に構築された手法です。
ですので、重回帰分析を実施するにあたっては、非常に制約が多く、理論に従わないデータがあったとしても、やむを得ず重回帰分析を行うしかないというのが現状としてあります。
しかし、多重ロジスティック回帰分析は重回帰分析と比較して制約条件が少ない為、分析しやすい多変量解析と言えます。
多重ロジスティック回帰分析は、単にロジスティック回帰分析とか、ロジスティック分析とよばれることもあります。
多重ロジスティック回帰分析の適用の条件とは?
- 独立変数(説明変数)には、あらゆるデータが適用できる。
- 従属変数(目的変数)は、0-1型の2値データでなくてはならない。
SPSSで多重ロジスティック回帰分析を実践する
それでは多重ロジスティック回帰分析を行っていきましょう。
まずは今回使用するデータを読み込みます。
今回のデータは、SPSSをインストールした際に付属しているサンプルデータを使います。
今回はサンプルデータのadl.savを使います。

adl.savは、脳卒中患者のリハビリ効果判定データです。
下記の解析条件で多重ロジスティック回帰(多変量ロジスティック回帰)を実施していきます。
- 従属変数(目的変数):退院後の発作(はい/いいえ)
- 独立変数(説明変数):治療グループ(治療/管理)、年齢、糖尿病(はい/いいえ)
解析の目的は、治療グループの違いが、退院後の発作の発生に影響を与えるか?、という設定をします。
つまり、群間比較を目的とした多変量ロジスティック回帰分析を実施します。
治療グループが群であり、年齢と糖尿病は交絡因子の可能性として、説明変数に含める、という意味になります。
SPSSのデータ(.sav)であれば、ダブルクリックすることでSPSSが立ち上がります。
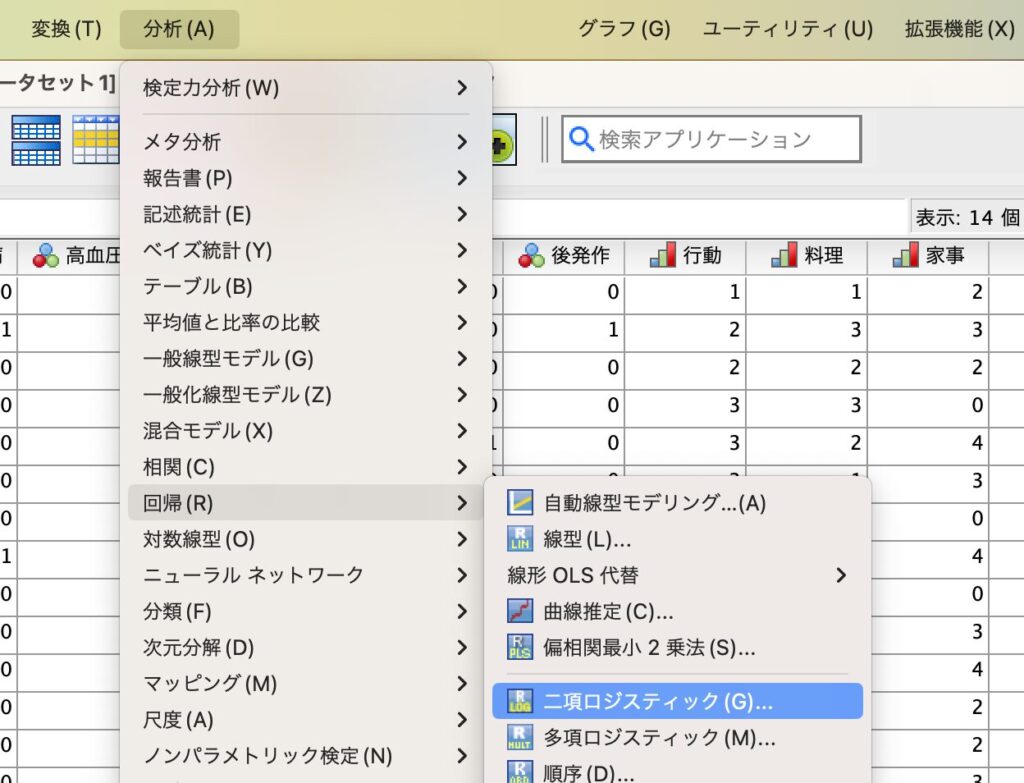
データをセットできたら、下図のように[分析]→[回帰]→[二項ロジスティック]を選択するとウィンドウが表示されます。
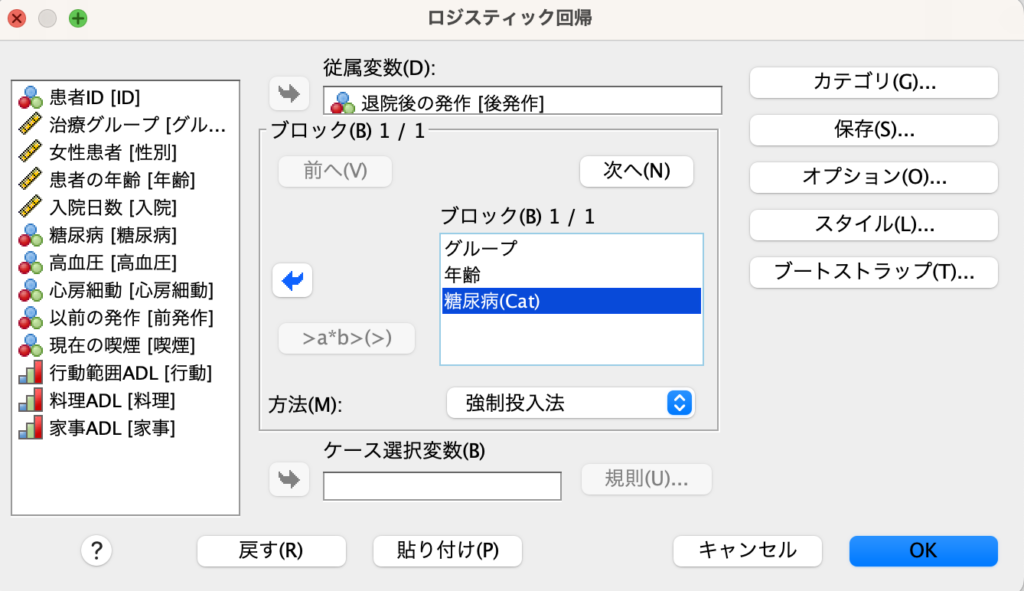
下図のボックスで従属変数に退院後の発作を入れます。
独立変数としたい治療グループ(治療/管理)、年齢、糖尿病(はい/いいえ)すべてを共変量に移動します。
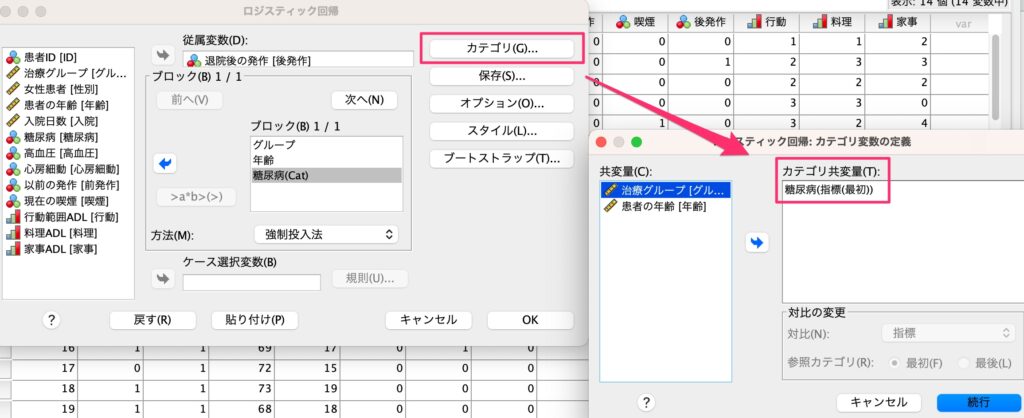
糖尿病はカテゴリカル変数として認識してもらいたいため、[カテゴリ]をクリックして[カテゴリ共変量]として糖尿病を指定します。
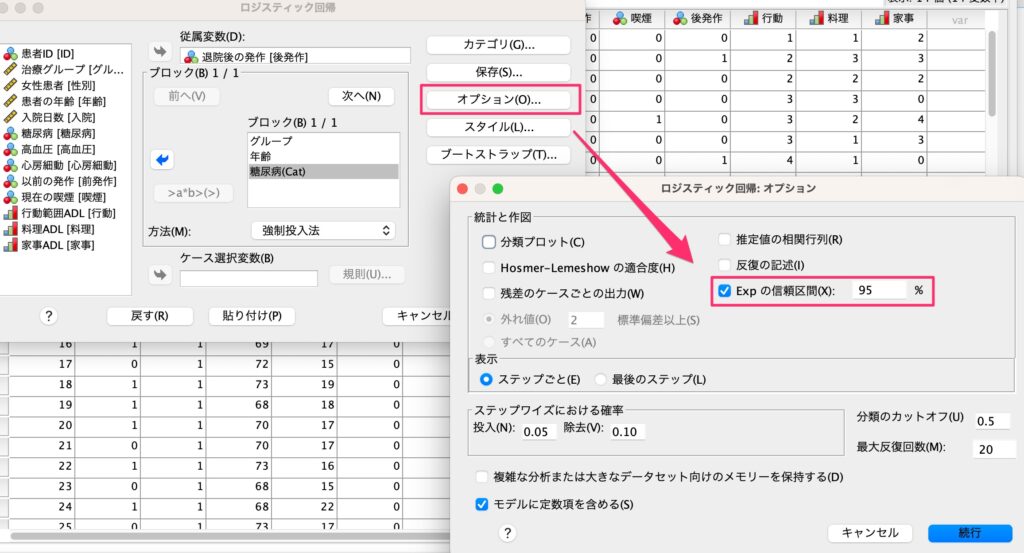
そして[オプション]から[Expの信頼区間]にチェックを入れます。
[Expの信頼区間]にチェックを入れることによって、オッズ比を出力することができます。
SPSSでの多重ロジスティック回帰分析の結果の読み方
下記が、多重ロジスティック回帰分析の結果です。
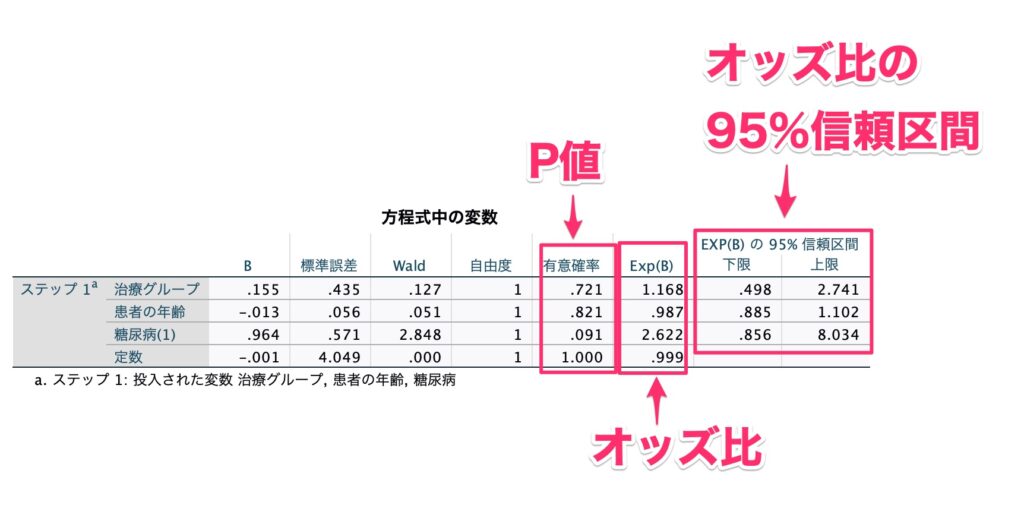
見るべきポイントは、「オッズ比」「オッズ比の95%信頼区間」「P値」の3つです。
今回は、解析の目的は、治療グループの違いが、退院後の発作の発生に影響を与えるか?、という設定をしていますので、メインの結果は「治療グループ」の行です。
今回の結果としては、オッズ比が1.168でありP値が0.721であるため、治療グループの違いは退院後の発作に対して違いをもたらすとは言えない、という結果になりました。
有意差がなかった時の結論の言い方に関しましては、こちらの記事をご覧ください。
SPSSでロジスティック回帰まとめ
今回はSPSSでロジスティック回帰分析を実施しました。
まずは正規分布かどうか等の制約がありませんので、比較的使用しやすい分析方法と言えます。
従属変数が2値のデータである事がポイントです。
独立変数の有意差だけではなく、得られたモデル式の適合度もしっかり見る事が重要です。
実際に分析して理解を深めてみましょう。











コメント
コメント一覧 (1件)
[…] 上記は、SPSSでロジスティック回帰分析を行った場合に出力される結果の一部です。 […]