分割表を解析するのに、とりあえずカイ二乗検定さえわかっておけば最低限は問題ないですね。
今回の記事は、そんなカイ二乗検定に関しての実践編。
EZRを使って実際にカイ二乗検定を実施してみましょう!
カイ二乗検定と同じ手順でフィッシャーの正確確率検定も実施してくれますので、併せてEZRでフィッシャーの正確検定を実施する方法も学んでいきましょう!
EZRでカイ二乗検定を実施するために必要となるデータを読み込む方法

まずは、カイ二乗検定を実施するために必要なデータを解説します。
カイ二乗検定のほかに分割表を検定するのは、フィッシャーの正確確率検定でしたね。
カイ二乗検定が分割表を検定する方法ということは、2種類のカテゴリカルデータが必要になります。
で、EZRで解析するためのデータ作成で重要なのが「1症例1行でデータを作成する」こと。
例えば性別データであれば、「男」か「女」というデータが各行に入ります。
(以下のイメージ参照)
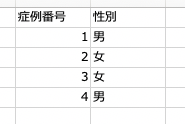
このようにデータを作っておけば、解析が可能になります。
カイ二乗検定の解析で使用するデータ
そして今回の記事で使うデータについても、1症例1行のデータになっています。
今回は肺がん(Lung Cancer)と喫煙の有無(Smoke)の関連を見ようと思います。
(データは架空のデータです。)
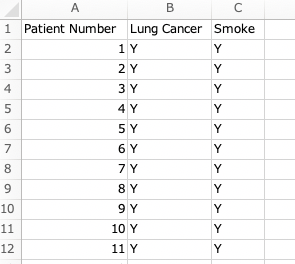
Lung CancerがYであれば肺がんあり、Nであれば肺がんなし、です。
同様にして、SmokeがYであれば喫煙あり、Nであれば喫煙なし、です。
これが80症例分あります。
EZRにカイ二乗検定を実施する基となるデータを読み込む
ではここから、EZRにデータを取り込みます。
まずは、サンプルデータを適切な場所に保存しておきましょう。
EZRを開き、「ファイル」→「データのインポート」→「ファイルまたはクリップボード, URLからテキストデータを読み込む」を選択します。
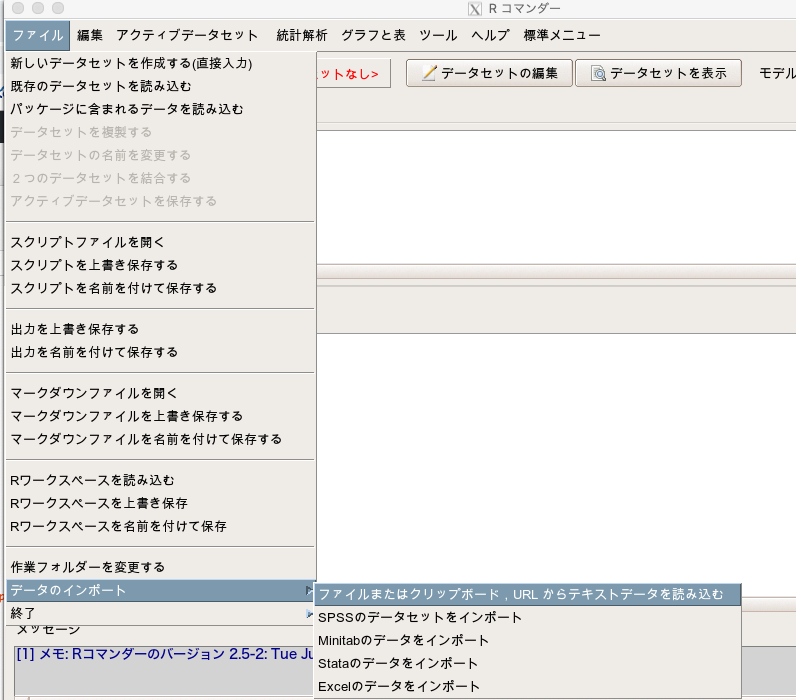
データセット名は「Chisq」にしましょう(実際はなんでもよい)。
そして「ローカルファイルシステム」と「カンマ」にチェックを入れてOKを押します。
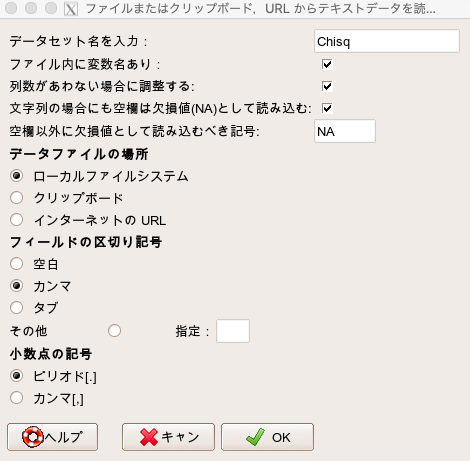
データセットが「Chisq」になっていることを確認し、「表示」を押してデータが正しく表示されれば取り込み完了です。
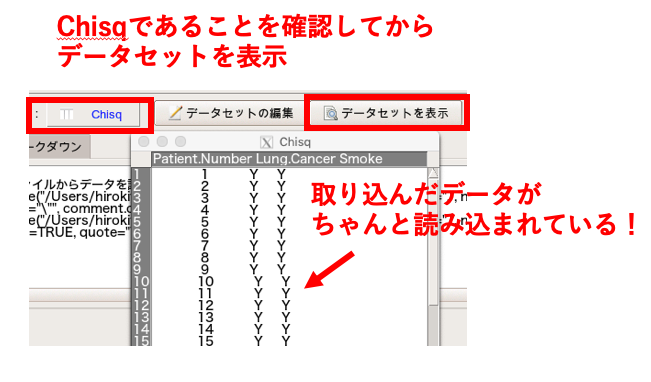
EZRでカイ二乗検定とフィッシャーの正確確率検定を実践する!

解析するための準備が整いましたので、早速カイ二乗検定を実施してみましょう。
カイ二乗検定を実施するには、以下の手順で行います。
「統計解析」→「名義変数の解析」→「分割表の作成と群間の比率の比較(Fisherの正確検定)」
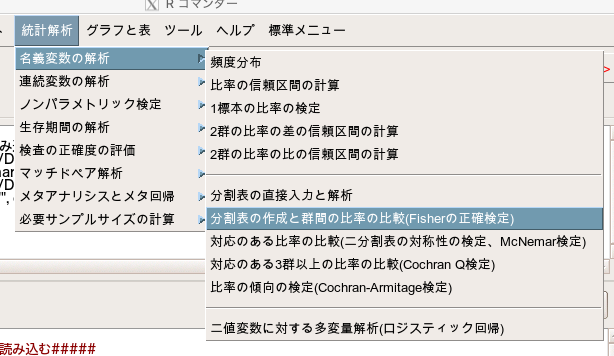
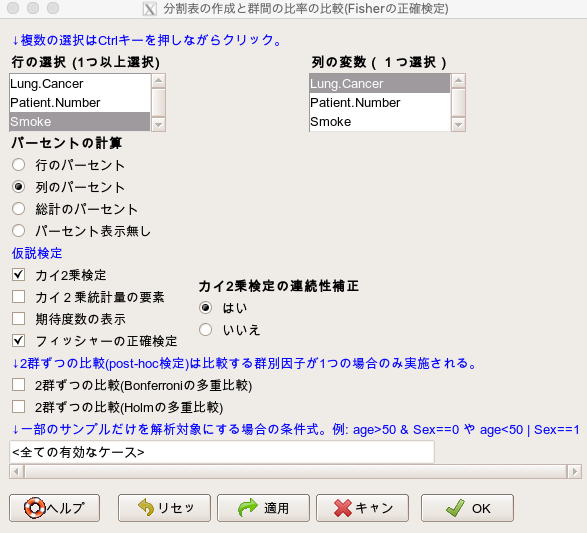
- 行の選択(1つ以上選択)で「Smoke」を選択します。
- 列の変数(1つ選択)で「Lung Cancer」を選択します。
- そして、仮説検定で「カイ2乗検定」にチェックを入れます。
- カイ二乗検定の連続性補正は「Yes」にしておきます。
- もしパーセント表示も必要であれば、必要な情報のパーセントを表示させましょう。
- Smoke(行で選択した変数)のパーセントが必要であれば「行のパーセント」を選択します。
- Lung Cancer(列で選択した変数)のパーセントが必要であれば「列のパーセント」を選択します。
他は、いじらなくてOKです。
これで解析を実行すると、以下の解析を自動で行ってくれます。
- 分割表の作成
- カイ二乗検定の実施
- フィッシャーの正確確率検定の実施
カイ二乗検定とフィッシャーの正確確率検定の結果の解釈をしよう
実際にカイ二乗検定が実施できました。
では、結果の解釈をしていきましょう。
分割表の結果解釈
まずは分割表の解析結果です。
以下の通り、4種類の結果が出ています。

- 「Smoke=NかつLung Cancer=N」が30例
- 「Smoke=NかつLung Cancer=Y」が20例
- 「Smoke=YかつLung Cancer=N」が10例
- 「Smoke=YかつLung Cancer=Y」が20例
今回のデータでは、SmokeがYかNの2種類のデータ、Lung CancerもYかNの2種類のデータですので、作成された分割表は2×2分割表と呼びます。
パーセント表示に関しても、確認してみます。

列のパーセント表示を選択したので、Lung Cancerに関してのパーセント表示がされています。
Lung CancerがNの集団では、喫煙の有無は25%(喫煙あり)と75%(喫煙なし)というように、差があります。
一方のLung CancerがYの集団では、喫煙の有無は50%であり、差がありません。
この分割表の結果を見るだけでも、肺がんの有無は喫煙の有無と関連がありそうに見えますね。
ではこの結果を、実際にカイ二乗検定結果を見てP値がどうなっているかを確認しましょう。
カイ二乗検定の結果解釈
カイ二乗検定の結果は、このようになっています。

ここでは、以下の3つが結果として出ています。
- カイ二乗値(Χ-squared)
- 自由度(df)
- P値(p-value)
2×2の分割表なので、自由度は1ですね。
そしてP=0.03767ですので、もし有意水準が0.05であれば、有意差ありという結果になり、帰無仮説を棄却することになります。
カイ二乗検定での帰無仮説は“2つの変数は独立である”であり、対立仮説は“2つの変数は独立ではない”です。
そのため、今回の結果は「肺がんの有無と喫煙の有無は独立ではない」という結果になります。
つまり、平易な言葉で言い換えると「肺がんの有無と喫煙の有無は関連がある」と言っていいですね。
カイ二乗検定はイェーツの連続性補正ありか補正なしか?
もしかしたら、「カイ二乗検定の連続性補正」について疑問を持ったかもしれませんね。
カイ二乗検定を実施するための画面で、連続性補正の有無を選択できました。
こちらの部分ですね。
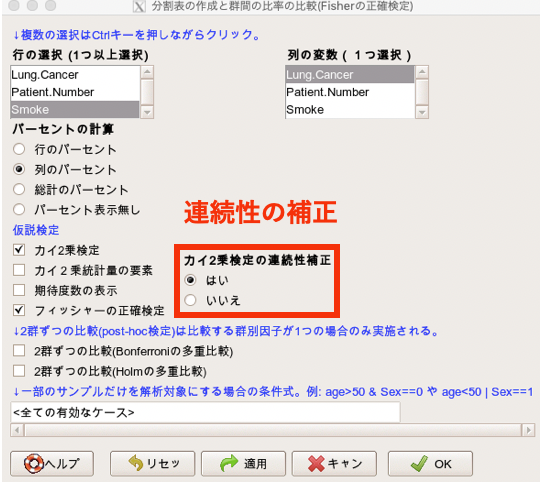
この連続性補正は、「イェーツの連続性補正」とも呼ばれています。
イェーツさんが開発したんですね。
気になるのは、この補正の有無で何が違うの!?ということ。
簡単にいうと、以下の通りです。
イェーツの連続性補正をすると、P値が大きくなる(有意差がでにくい)
えっ!!!
じゃあ連続性補正をしないほうがいいのでは・・・という風に思いましたか?
ちゃんとデータを取る前に解析計画書で「イェーツの連続性補正をしないカイ二乗検定を実施する」というように規定していれば、イェーツの連続性補正をしなくてOKです。
しかし、そのように事前に計画を立てていない探索的な解析では、基本的には有意になりにくい解析をするべきです。
というのも、有意になりやすい検定を実施して「有意差があった!」という結論を出しても、「え、その検定方法だから有意になっただけでしょ!?」という疑問を払しょくできないからです。
そのため、事前にイェーツの連続性補正をしないで解析することを宣言していない限りは、連続性補正をした解析を実施しましょう。
フィッシャーの正確検定の結果も出力される
カイ二乗検定を実施する際のEZRのボタンが「分割表の作成と群間の比率の比較(Fisherの正確検定)」とあった通り、フィッシャーの正確確率検定の結果も出力されます。

フィッシャーの正確検定の方が、P値以外にもかなりの情報が出力されていますね。
- P値(p-value)
- 対立仮説(alternative hypothesis)
- 95%信頼区間(95 percent confidence interval)
- オッズ比(odds ratio)
最後に出力されている表のP値だけを確認するのもいいですが、できれば95%信頼区間などもちゃんと確認したほうがいいですね。
ぜひ、確実な解釈をしましょう!
EZRでは3群以上の場合でもフィッシャーの正確確率検定を実施できる!
意外と知られていないのですが、EZRでは3群以上の場合でもフィッシャーの正確確率検定を実施してくれます。
JMPだと2*2分割表でしかフィッシャーの正確確率検定は実施できないのですが(JMP Proならできる)EZRでは可能です。
試しに、下記のような架空のデータ(Treatmentが0,1,2の3群)で実施してみます。

解析手順は同じなので、割愛しますね。
解析を実施すると、以下のように3行2列の分割表が作成されます。
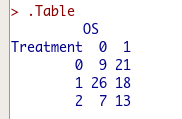
そして一番最後には、フィッシャーの正確確率検定の結果が表示されます。

以上のように、EZRでは3群以上の場合でもフィッシャーの正確確率検定を実施してくれることがわかりましたね。
EZRでカイ二乗検定とフィッシャーの正確確率検定まとめ

今回は、EZRでカイ二乗検定を実施しました。
データさえちゃんと作りこめば、特に難しいことはありませんでしたね。
また、3群以上の場合でもEZRではフィッシャーの正確確率検定も実施してくれます。
ぜひ解析の仕方をマスターしましょう!!














コメント
コメント一覧 (3件)
[…] […]
[…] 分割表の解析をEZRで実践する方法を、別記事で解説しています。 […]
[…] […]