統計的仮説検定にはαエラーとβエラーという2種類のエラーがあります。
このうち、βエラーに関する概念として「検出力（Statistical Power）」というものがあるのをご存知ですか？
検出力を求めることや論文等に表記する機会はほとんどないといっても良いかもしれませんが、医療系の研究において必須とも言える、サンプルサイズの計算では検出力を設定しなければならいなものです。
サンプルサイズの計算において、設定すべき検出力の基準は概ね決まっていますが、その意味を知ることでサンプルサイズ計算の必要性や仮説検定に対する理解が深まります。
この検出力についてわかりやすく解説していきます。
Contents
検出力とβエラーの関係を理解する前に有意水準とαエラーの関係をおさらい
医療系の分野で仮説検定を行う場合、有意水準は5%に設定されることが一般的です。
仮説検定は、帰無仮説を前提として、データから算出した統計量（t値など）をもとにして外側確率（p値）を求め、p値が有意水準を下回っていれば帰無仮説を棄却するという流れで行われます。
p値とは、データから算出した統計量と同等以上に稀なことが、帰無仮説を前提としても起こりうる確率、と言い換えることもできます。
帰無仮説が正しいとしてもp値程度にはデータから算出した統計量と同等以上に稀なことが起こりうる、ということはすなわち、帰無仮説を誤って棄却する可能性があることを意味します。
確率を使って判断するので一定の間違いは仕方ないという考えですね。
二項検定によるαエラーの具体例
具体例で見てみましょう。
今、従来はリハビリによる改善率が20%程度の障害に対し、新しい方法で改善率が高まると考えているとします。
この新しい方法を10人に試して、改善率が良化しているか検証することにしました。
結果は改善か否かの2値ですので二項検定が使えます。
悪化することはないと考え片側検定を行うとすると、帰無仮説は「母改善率は20%を上回らない。」となります。
10人の結果について、帰無仮説の上限である20%を用い、2項分布で確率を計算すると1人から3人程度に改善が見られる確率が高くなっています。
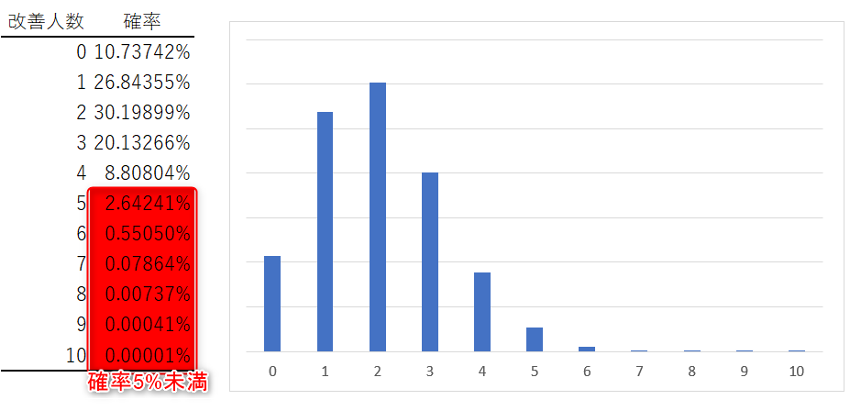
赤く塗りつぶしているところに注目して下さい。
改善人数が5人以上になる確率は約3.28%です。
そのひとつ上の4人の改善も含めると、確率は10%を超えてきます。
有意水準を5%に設定するならば、10人中5人以上の改善で有意水準を下回りますので帰無仮説が棄却されることになります。
と同時にこの場合は約3.28%のαエラーを許容することになります。
検出力（Statistical Power）とは何なのか？βエラーとの関係をわかりやすく解説
αエラーは真実は差がない時に帰無仮説を誤って棄却してしまうことでしたが、βエラーは真実は差があるのに帰無仮説を誤って棄却できないことです。
この誤りは対立仮説の具体的状況により起こりやすさが変化してしまいます。
どういうことか、具体例で見ていきましょう。
二項検定によるβエラーの具体例を元にして検出力を考える
帰無仮説「母改善率は20%を上回らない。」に対応する対立仮説は「母改善率は20%を上回る。」です。
「母改善率は20%を上回る。」という仮説には、母改善率が20%を超えて100%まであらゆるケースが含まれています。
仮に、真の母改善率が30%だとすると、10人に試した場合の改善人数の確率は以下のようになります。
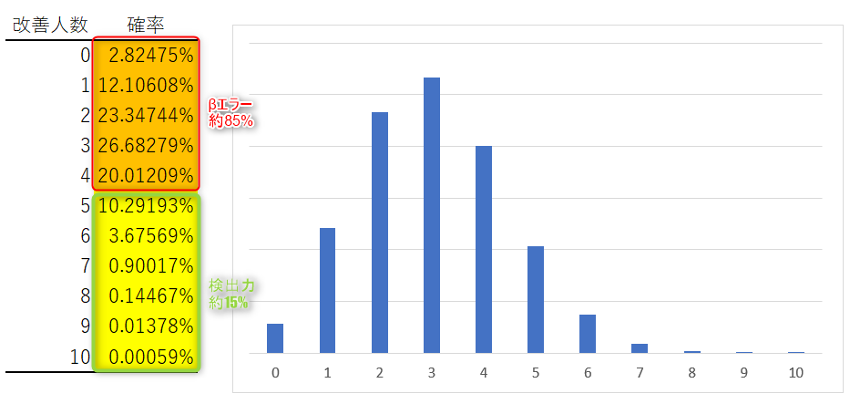
有意水準5%のもと帰無仮説を前提にした棄却域は、前述の通り、5人以上の改善。
その場合、真の母改善率30%とすると、約85%の確率で改善人数が5人未満となります。
すなわち、85%の確率で帰無仮説を棄却できないことになります。
この85%がβエラーです。
逆に、約15%の確率で改善人数が5人以上となります。
すなわち、15%の確率で帰無仮説を棄却できることになります。
この15%が検出力なのです。
真の母改善率がもっと高いときはどうでしょう。
真の母改善率が80%だった場合で考えてみましょう。
10人に試した場合の改善人数の確率は以下のようになります。
この場合、改善人数が5人未満となり、帰無仮説を棄却できない確率は1%未満になります。
すなわち、βエラーは1%未満です。
それに対し、改善人数が5人以上となり、帰無仮説を棄却できる確率は99%以上となります。
すなわち、検出力は99%以上という確実性の高い検定になります。
このように、検出力は真の母数が帰無仮説の値と乖離していればいるほど高くなるのです。
直感的には、大きな差があるものほど、より正しく検出できるということです。
検出力が低いとはどういうことを意味するのか？
先程の例を見た通り、検出力とβエラーは表裏一体です。
検出力＝1-βエラー
という数式が成り立つため、検出力が低いということは、βエラーが大きいということを示します。
そのため、検出力が低い＝本当は治療間に違いがあるのに統計学的検定で有意差が出る確率が低い、という事が言えます。
検出力はいつも80%や90%にしなきゃいけないの？
論文を読んでいたりすると、検出力は80%や90%に設定している事が多いです。
この検出力80%の意味は「本当に治療間で違いがある場合に、10回試験をやったら8回は有意差が出ることを期待する」ということを意味します。
つまり言い換えると、企業側（研究者側）のリスクをどれだけに設定するのか、ということにもつながるわけです。
「この試験（研究）は絶対に失敗したくない！」と思えば、90%の検出力を確保する必要があるかもしれません。
ですが一方で、「必ずしも有意差でなくてもいいかも」という試験であれば、70%と設定してもいいわけです。
私自身、薬の開発のPhase2試験で検出力70%で試験を組んだこともありますので、必ず検出力を80%や90%にしなきゃいけない、ということではないのです。
検出力を高める方法
では、検出力を高めるにはどうしたらいいのでしょうか？
具体的には「有意水準の変更」や「サンプルサイズを大きくする」というアイデアが挙げられます。
検出力を高める方法1：有意水準を変更する
検出力は対立仮説を正しく採択する確率ですので、高いに越したことはありません。
ではどうすれば検出力を高めることができるでしょうか。
手っ取り早いのは有意水準をより大きな値に変更することです。
上記の通り、検出力は帰無仮説と有意水準を前提として決まりますので、αエラーとβエラーまたは検出力はトレードオフの関係にあります。
有意水準がより高い値であれば、対立仮説を前提とした確率計算においても、棄却域に入る確率が高くなるため検出力も高くなります。
しかし理論上は有意水準を大きくすれば件出力が上がると分かっていても、現実世界では有意水準は5%と設定するのが鉄則なので、検出力を高めるために有意水準を大きくする方法を取ってはいけませんね。
検出力を高める方法2：サンプルサイズを大きくする
検出力を高めるために、実際に行える方法はサンプルサイズを大きくすることです。
前述の例で、被験者を10人から20人に増やした場合を見てみましょう。
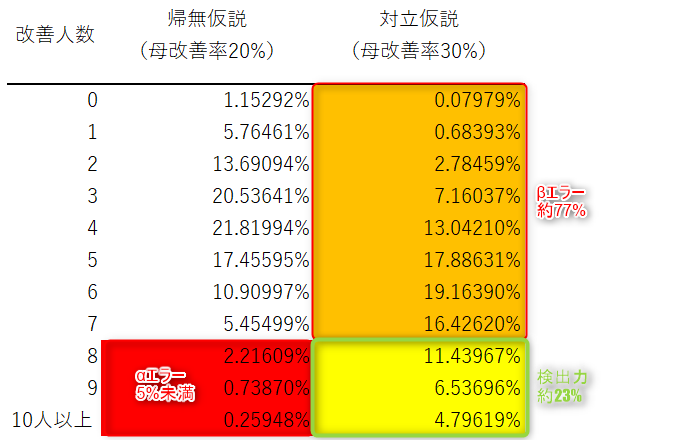
帰無仮説の母改善率20%を前提に確率を求めると、改善人数が8人以上で5%を下回ります。
つまり、改善人数が8人以上で帰無仮説は棄却されることになります。
そして、対立仮説のほうを真の母改善率が30%であるとした場合、改善人数が8人未満になる確率（βエラー）は約77%となります。
改善人数が8人以上となる確率（検出力）は約23%ですから、検出力が被験者10人のときに比べて、0.05程度向上していることが確認できます。
このように、サンプルサイズを大きくすると検出力が高くなります。
このことを利用して、サンプルサイズの計算を行っています。
まとめ
検出力は、学会発表や論文において、直接言及されるケースは少ないかもしれません。
しかしながら、検出力は仮説検定の根幹をなす概念のひとつです。
検出力は母集団がどのような状況にあるかによって変化するものですから、正確な値を知ることはできませんが、研究仮説を設定する段階で母集団の状況をしっかり考慮することでサンプルサイズの計算を通して高い検出力を保つことが可能です。
より良い量的研究のため検出力についてもしっかり理解しておきましょう。
EZRで検出力を計算する方法もお伝えしていますので、併せてご覧くださいませ！
第1章：臨床研究ではなぜ統計が必要なのか？計画することの重要性
第2章：研究目的をどれだけ明確にできるのかが重要
第3章：p値で結果が左右される時代は終わりました
第4章：多くの人が統計を苦手にする理由
第5章：統計を使えるようになるために今日から何をすれば良いか？
第6章：統計を学ぶために重要な環境
もしあなたがこれまでに、何とか統計をマスターしようと散々苦労し、何冊もの統計の本を読み、セミナーに参加してみたのに、それでも統計が苦手なら…
私からプレゼントする内容は、あなたがずっと待ちわびていたものです。
