この記事では、Wald検定に関してお伝えしていきます。
医療統計において、予後に対するリスク因子を探るため、ロジステック回帰分析やCoxの比例ハザード分析を行うことがよくありますね。
SPSSなどの統計ソフトウェアを用いて、ロジスティック回帰分析やCoxの比例ハザード分析を行った場合、独立変数の有意性を確認する結果で、Waldという項目が出力されます。
これはWald検定の検定統計量を示しているのですが、そもそもWald検定というのはいったいどういうものなのでしょうか?
Wald検定についてわかりやすく解説していきます!
Waldは検定統計量なのでP値計算に使われる!尤度比検定とどっちがいいの?

上記は、SPSSでロジスティック回帰分析を行った場合に出力される結果の一部です。
投入した独立変数が有意か否かは有意確率(p値)の列を確認することでわかります。
この例で、5%有意水準とするならば、sexとph.ecogがアウトカムの発生に有意な影響を与えていると言えますね。
さて、このp値はどのように計算されているのでしょうか。
Waldの列に注目してください。
Waldの値の大小と有意確率(p値)の大小が対応していることが分かりますね。
有意性を示しているsexやph.ecogのWaldが他の変数のものより大きくなっています。
そうなんです、p値とリンクしているWaldは検定統計量なのです。
Wald検定と尤度比検定だったらどっちを使うの?
Wald検定と同様に、尤度比検定の結果も同時に出力される統計ソフトもあります。
じゃあWald検定と尤度比検定とどっちを使えばいい?となりますが、それには正解はありません。
ただ一つ言えるのは、「論文には割とWald検定が使われていることが多い」ということ。
なので、この記事でWald検定について理解して、Wald検定の結果を用いていきましょう。
Wald検定の検定統計量の計算方法
検定統計量であるWaldはどのように計算されているのでしょうか。
それは以下になります。

![]()
この数式に上の表の値を代入すると
概ねWaldの値と一致します。
(完全に一致しないのは、小数第4位で四捨五入しているため)
そして、Waldが自由度1のカイ2乗分布に従うことを利用してp値を算出しています。
Wald検定の帰無仮説, 対立仮説
話は前後しますが
Wald検定の帰無仮説は「母パラメータはβである(通常は0を仮定)。」になります。
これは、独立変数が従属変数に影響を与えていないということになります。
Wald検定の対立仮説は「母パラメータはβではない(通常は0を仮定)。」になります。
これは、独立変数が従属変数に影響を与えているということになります。
上記の仮説とWaldの数式をもう一度じっくり見てみてください。

![]()
推定値から仮説の母パラメータを引いて、標準誤差で割っています。
これがt検定などのパラメトリックな検定で行う標準化と同じであることに気付きましたか。
そして、標準化した値を2乗しています。
この2乗した値がカイ2乗分布に従うとしているということは、推定値に正規分布を仮定していることになります。
では、質的なアウトカムに対する分析である、ロジステック回帰分析やCox比例ハザード分析でなぜ正規分布が出てくるのでしょうか?
Wald検定が使われる場面:なぜロジスティック回帰分析やCox比例ハザードモデルで使われる?

ロジステック回帰分析とCox比例ハザード分析は、どちらも質的なアウトカム、例えば、生存か否か、再発か否かというような2値の質的なアウトカムに対する分析です。
しかし、前者はエンドポイントにおける分析であるのに対し、後者は時間経過を考慮に入れた分析であるので随分異なる分析です。
また、医療統計でよく使われる分析ではこの2つが代表的ですが、他にもWald検定が行われる分析はいくつも存在します。
このように異なる分析で同じWald検定が使われるのはなぜでしょうか。
それは、これらの分析の推定方法が同じだからです。
その推定方法とは、「最尤推定(最尤法)」です。
Wald検定が使われる最尤推定とは?
最尤推定とは、観測されたデータから、それらデータの従う確率分布の母パラメータを推定する方法です。
・・・と言っても、ピンとはきませんね。
具体例で説明しましょう。
コイン投げのような、2つの結果のいずれかが発生する試行を繰り返す場合、その確率は二項分布に従います。
ロジスティック回帰分析やCox比例ハザード分析も、「生存か否か」「再発するか否か」という2つの結果のいずれになるかを問題にしていますから、根底には二項分布の発想があります。
独立変数の状況により(例えば、ある薬剤を処方されていたかどうか)、確率の異なるコインを投げていると捉えることもできます。
表の出る確率が50%のコインをn回投げてx回表の出る確率は二項分布により
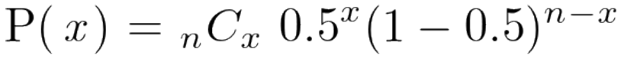
となります。
パラメータである「表の出る確率」が与えられている前提で、確率変数である表の出る回数についての確率を計算できます。
最尤推定はこのパラメータと確率変数の捉え方を逆転させます。
例えば、表の出る確率(θ)が不明のコインを40回投げてみたところ、表が10回観測されたとします。
この状況を数式で表現すると

となります。
式の構造自体は二項分布のままです。
違いは、確率変数であったxが観測された定数となり、パラメータが未知の値θとなっている点。
このように確率分布の確率変数が定数となり、パラメータが未知数となったものを尤度関数(likelihood function)とよびます。
頭文字からLを使って表現します。
二項分布の最尤推定
尤度関数はパラメータが変化したときの観測値の出現確率を表現しています。
上の尤度関数をグラフにすると
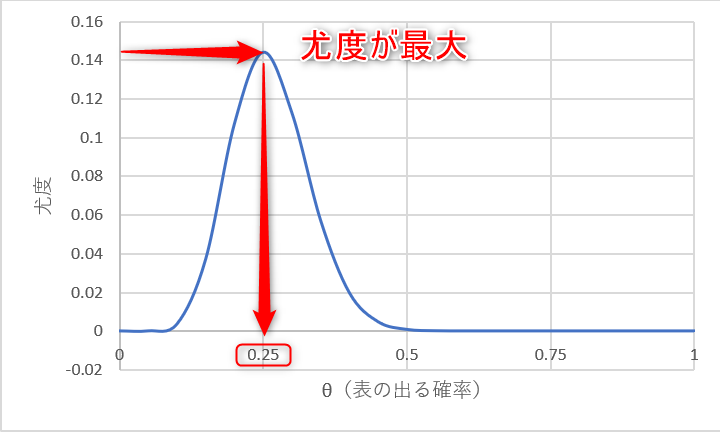
θが0.25のときに尤度関数の値が最大になっているのが見て取れます。
つまり、40回コインを投げて表が10回観測されるという事象は、表の出る確率が25%のときに最も起きやすいということになります。
このことから、投げたコインの表の出る確率は25%であると推定するのが最尤推定です。
観測値を最も出現させやすい(尤度関数の値が最も大きい)パラメータを推定量とする方法とも言えますね。
最尤推定量の分布
最尤推定によって推定されるパラメータを最尤推定量とよびます。
この最尤推定量にはWald検定の根拠となる重要な性質があります。
先ほどの40回コインを投げる例で、真のパラメータの値(表の出る確率)が40%だったとします。
このとき、40回コインを投げる試行により、観測される表の出る回数の分布は二項分布により
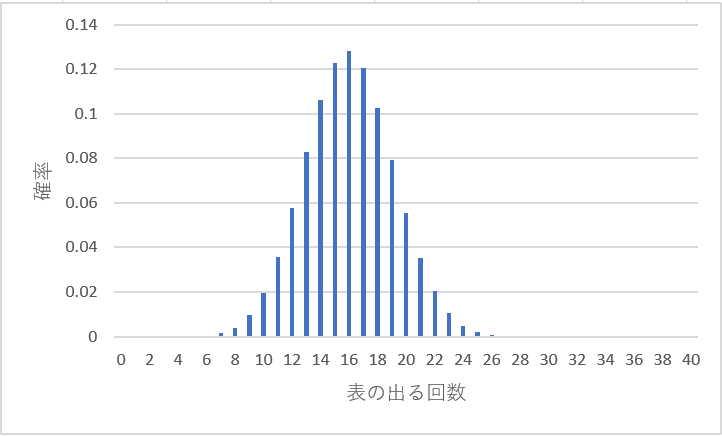
このようになります。
そして、各観測値に対して、最尤推定により求まる最尤推定量の分布は
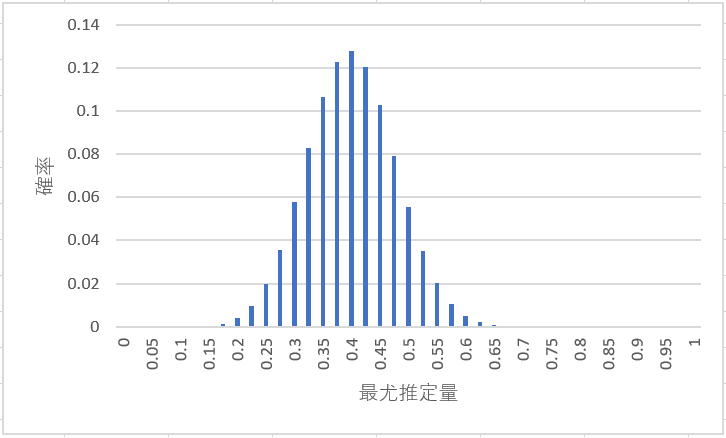
となります。
最尤推定量の漸近正規性を考えるとWald検定になる
最尤推定量の分布のかたちが釣鐘型の正規分布に似て見えますね。
最尤推定により求まるすべての最尤推定量の分布は分析対象のサンプル数が十分に大きくなると正規分布に近似することができます。
数学的な証明は難解ですが、上のグラフのイメージから実感できるのではないでしょうか。
Wald検定は、最尤推定量の漸近正規性を根拠として、標準化と同じ処理をした上でカイ2乗分布により検定しているのです。
まとめ

ロジスティック回帰分析やCox比例ハザード分析に代表される、最尤推定を用いた分析では、
各独立変数の有意性を検証するため、Wald検定を行います。
確率の概念を利用した最尤推定は、一見難しそうに感じますが、最尤推定量の漸近正規性という都合の良い性質を根拠に、カイ2乗分布というオーソドックスな分布で検定できる点でとても使い勝手の良い検定です。













コメント