この記事では、一様分布について詳しくお伝えします。
- 一様分布ってどんな分布？
- 一様分布の平均値や分散はどうなっているの？
といった疑問についてお答えしていきます！
正規分布よりは重要性が落ちる一様分布ですが、この知識を知っておくことで医療統計の様々なところで応用できるため、ぜひ理解していきましょう！
Contents
一様分布とは？サイコロの例でわかりやすく！
一様分布とは、ある区間における全ての事象の起こる確率が等しく生起する分布のことです。
言い換えると、確率密度関数が常に一定の値である確率分布を一様分布という。
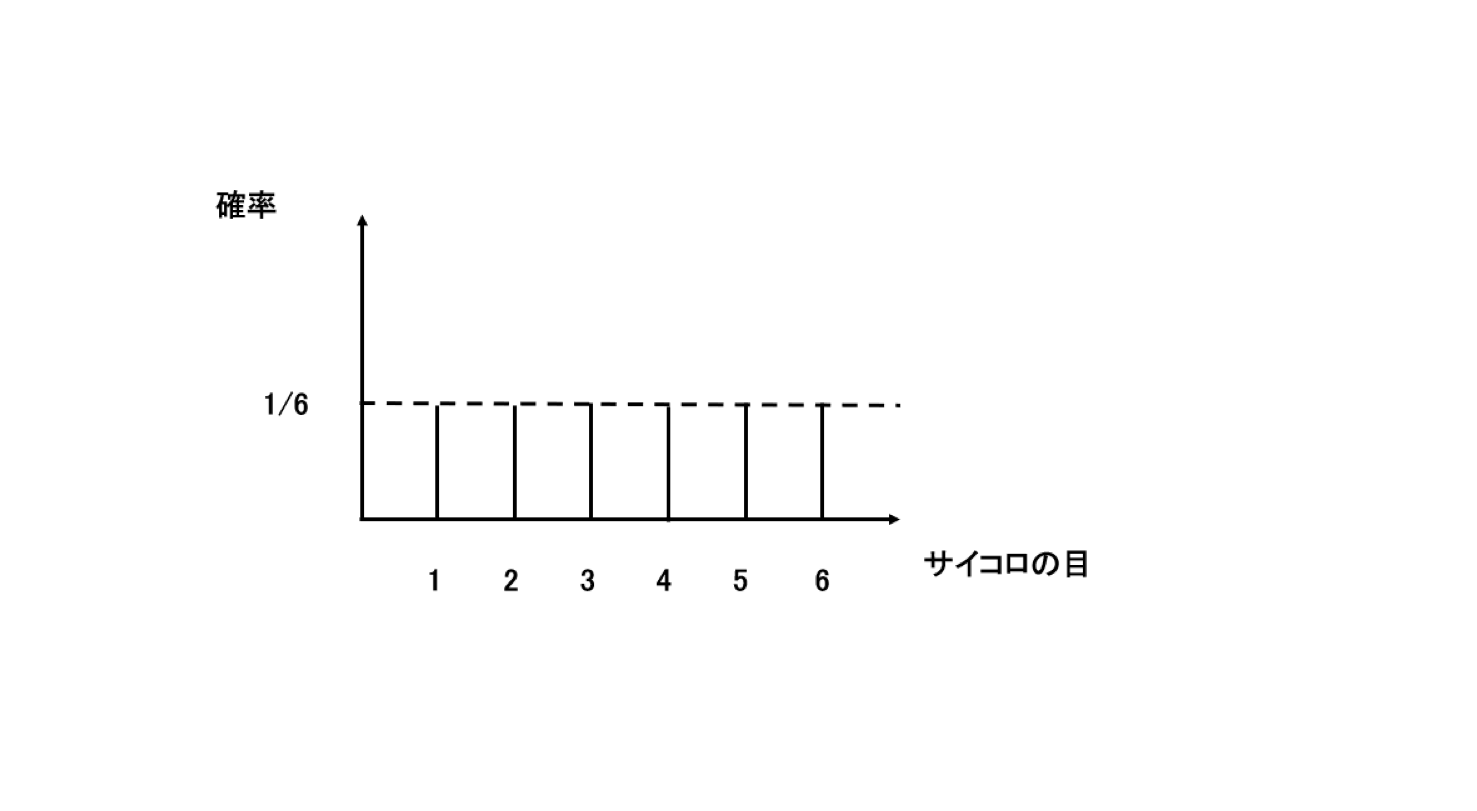
例えば、６面体のサイコロを振った場合に１から６の目が出る確率が同様に確からしいとすると、どの目が出る確率もみんな １／６ となりますが、これが一様分布の例です。
サイコロの確率密度関数をグラフにするとこんな感じ。
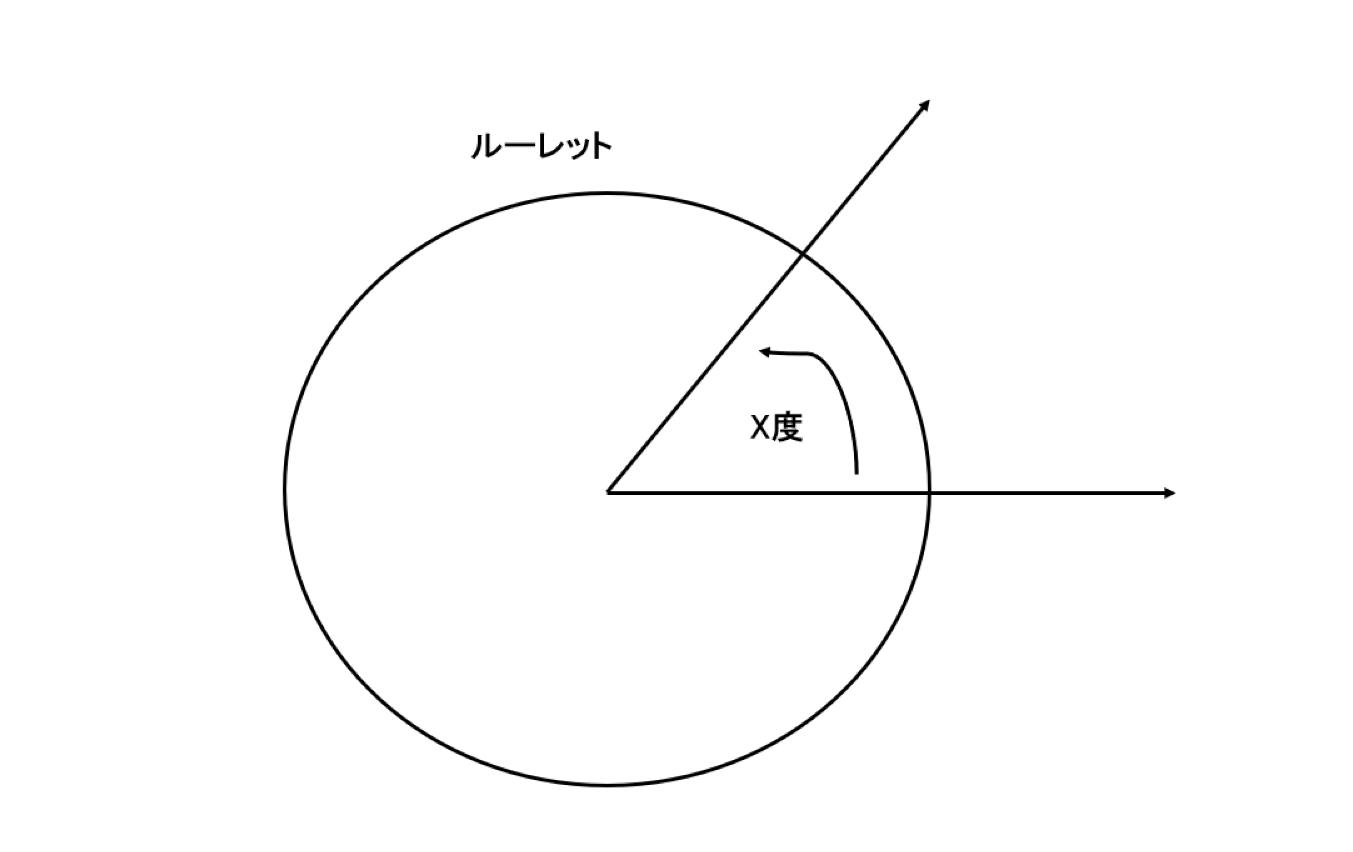
下の図のようなルーレットを考えます。
連続的に円を描き、0度から360度までのどこかで止まるとする。
この場合の確率密度関数は、こんな感じ。
一様分布は確率密度関数が常に一定の値である確率分布で形がシンプル
上記で説明したとおり、一様分布はある区間の中の値が同じ確率で生起する分布のことです。
確率密度関数は常に一定の値になります。
確率変数が離散値を採る場合を離散一様分布、確率変数が連続値を採る場合を連続一様分布。
グラフに書くと、離散一様分布であれば点が横に並び、連続一様分布であれば横線となる。
一様分布はどこで使われている？
一様分布は特殊な分布で、活用方法は限定されている。
例えば、生命保険料を計算する際に基礎となる死亡率を計算する場合、1年を通して死亡が一様に発生（一様分布に従う）として計算したり、不確かさの評価で範囲内の測定値を一定
と仮定する場合に使用したりします。
また、モンテカルロシミュレーションなど様々な応用がなされている乱数という概念でも一様分布の考え方が使われている。
ちなみに乱数では、以下のような形で一様分布の考え方が出てきます。
ある数列 x1, x2, …, xn から次の数列の値 xn+1 が予測できない数列のことを乱数列といいい、各要素を乱数というが、例えば0から1までの区間内で全ての実数が同じ確率で現れるような連続一様分布に従う乱数のことを一様乱数と呼ぶ。
もう一つ例をあげると、物理学にはエントロピーという概念があり、これは原子や分子の乱雑さの尺度を表す量のことです。
このエントロピーは確率変数が一様分布である場合に最大となることが示される。
一様分布に従うということは、言い換えると、どの事象が起きる確率も等しいということなので、事象について事前に全く手がかりがないということを意味するから、そのエントロピーが最大となるのは物理的に考えれば当然とも言える。
以上のように一様分布はそれ自体何かの計算に応用されるという場合は少なく、一様分布を仮定してそれを基にさらに発展した概念を構築したり、ある概念の特殊な場合に一様分布が関与していたりと、間接的に出てくる場合が多いです。
それでは、離散一様分布の確率関数はどうなるでしょうか。
確率変数Ｘが離散一様分布に従うとき、確率関数（Ｘ＝ｋとなる確率Ｐ（Ｘ＝ｋ））は、Ｎを確率変数Xの取りうる個数とすると次のように表される。
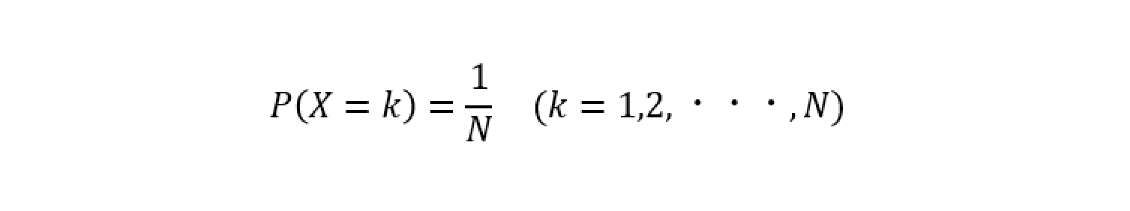
確率変数Xがa≦X≦bにおける連続一様分布に従うとき、確率密度関数は次のように表される。
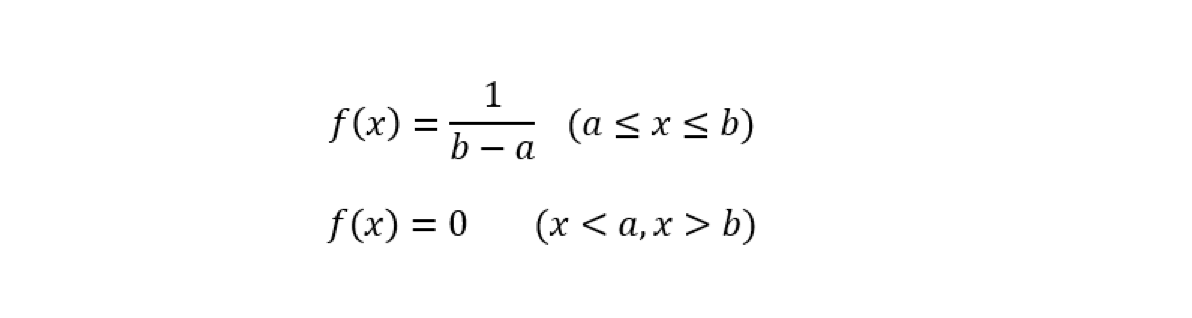
一様分布の期待値（平均）と分散はどうなっている？
一様分布の期待値（平均）と分散は離散型と連続型で異なる
一様分布の期待値（平均）と分散はどうなっているのでしょうか。
例えば、離散一様分布となるサイコロの例で考えると、1が出る目の確率が1/6、2が出る目の確率が1/6、・・・、6の目が出る確率が1/6なので、期待値（平均）は、1×1/6＋2×1/6＋・・・＋6×1/6＝3.5となる。
また、1が出る目の確率が1/6、2が出る目の確率が1/6、・・・、6の目が出る確率が1/6なので、分散は以下のとおり。
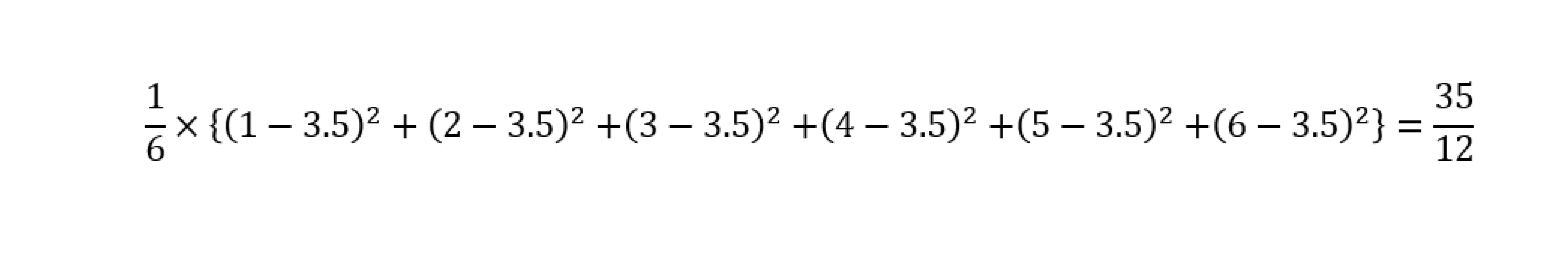
次に、連続一様分布となるルーレットの例で考えると、期待値（平均）は、180であることが直観的に分かると思います。
ところがルーレットの例では分散は直感的には求まりませんが、答えだけ書くと10800です。
一様分布の期待値（平均）と分散の求め方・証明は？
一様分布の期待値（平均）と分散は比較的簡単に求まる。
まず、離散型一様分布の期待値（平均）の求め方・証明は以下の通り。
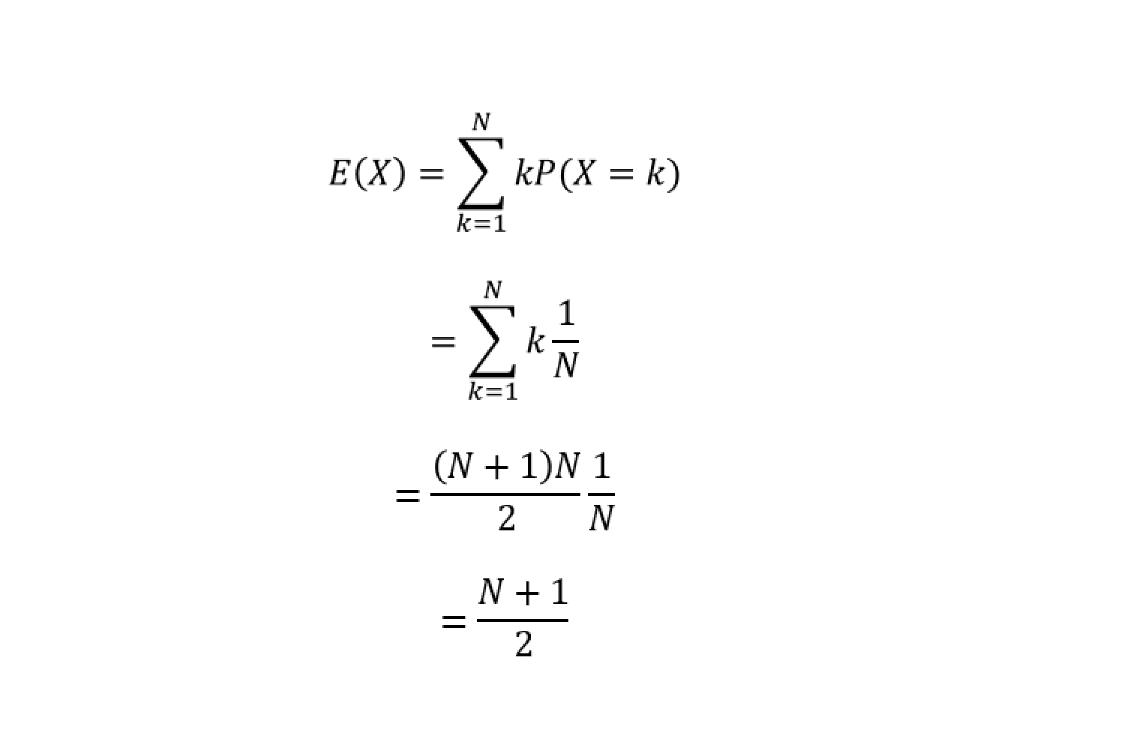
次に、離散型一様分布の分散の求め方・証明は以下の通り。
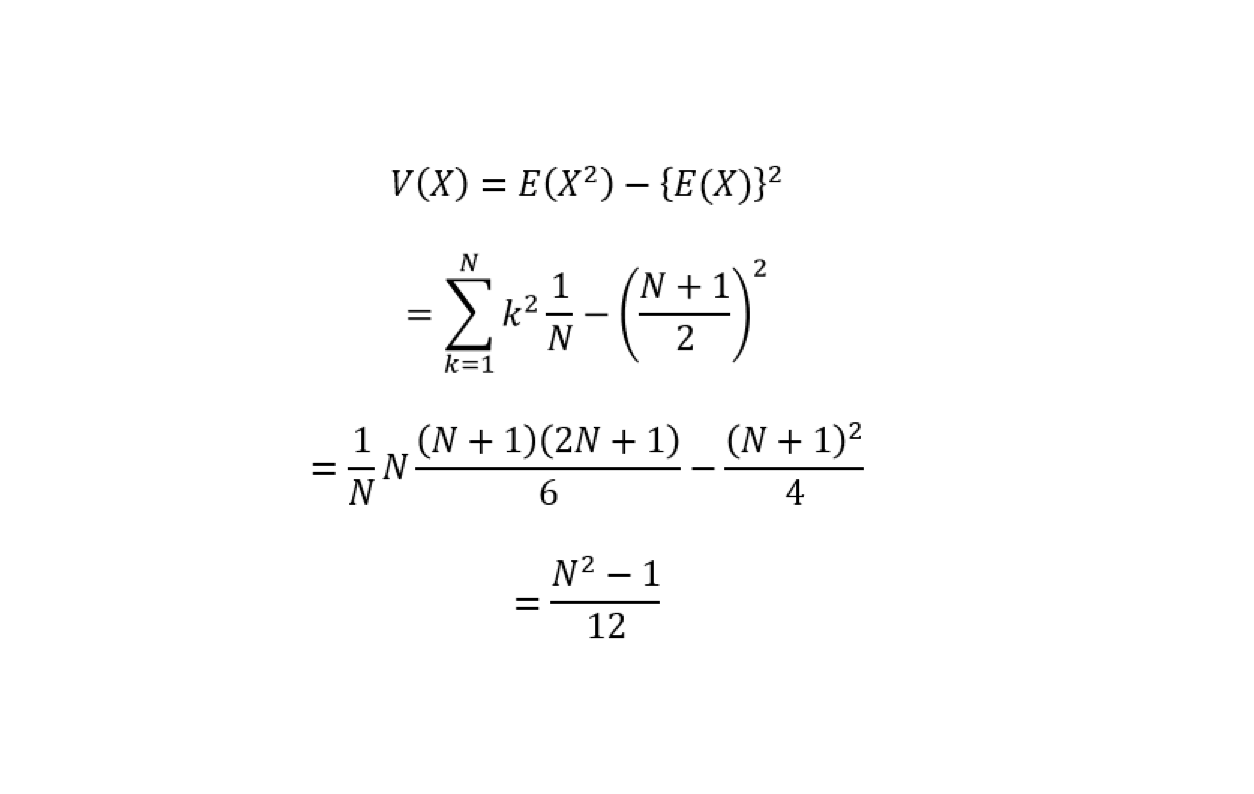
連続型一様分布の期待値（平均）の求め方・証明は以下の通り。
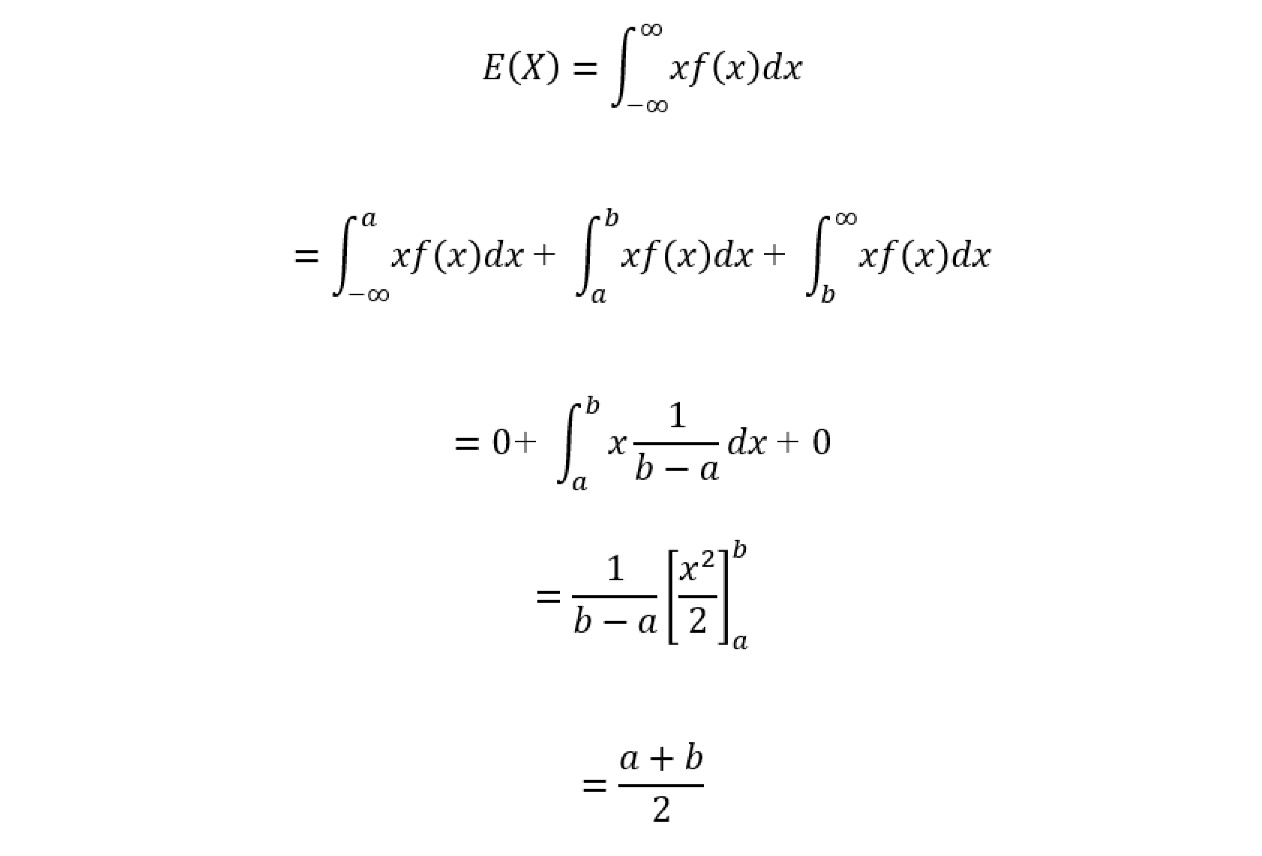
そして、連続型一様分布の分散の求め方・証明は以下の通り。
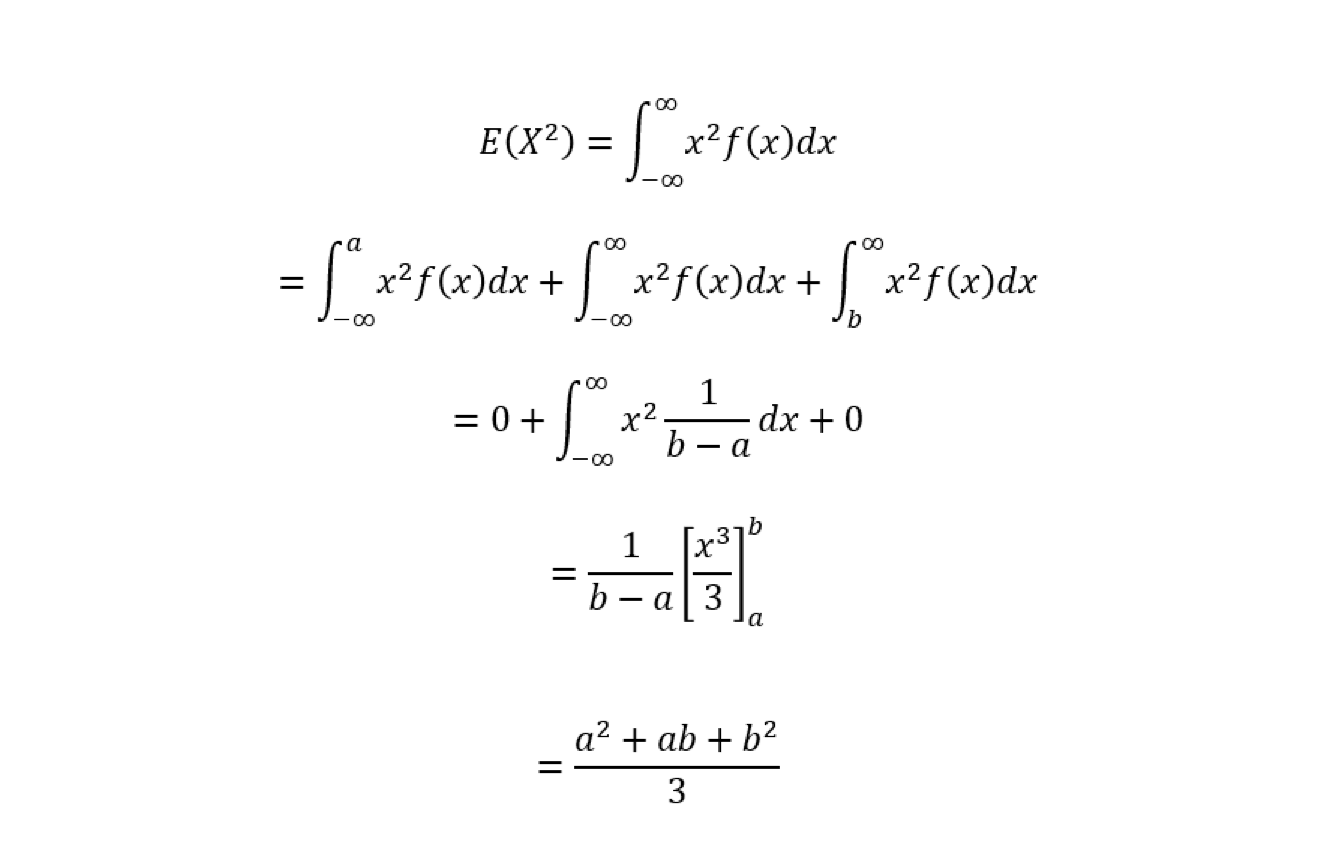
よって、
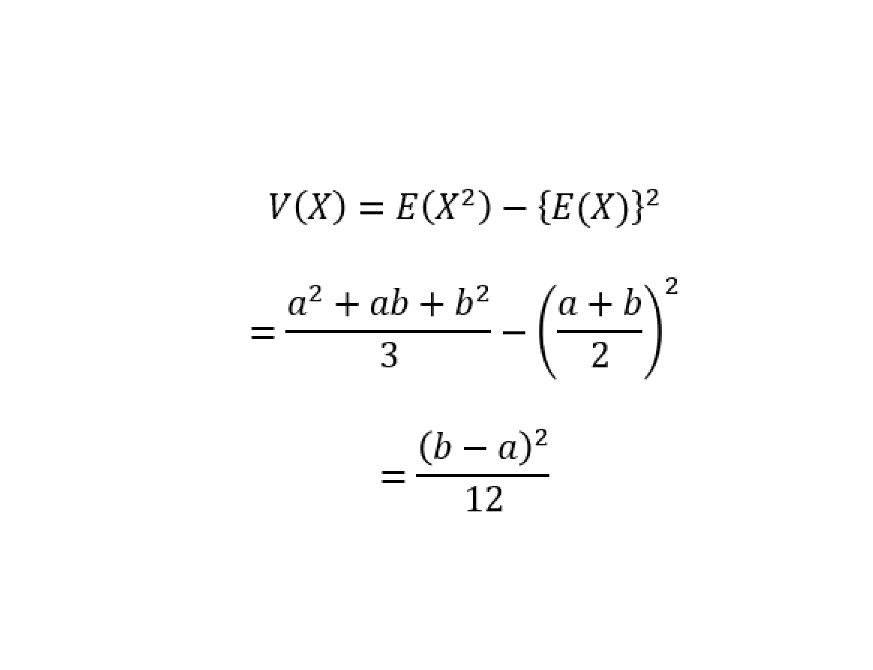
一様分布についてまとめ
いかがでしょうか。
一様分布について理解できたでしょうか。
一様分布とは、確率密度関数や確率関数が常に一定の値である確率分布で、直接の応用は限定的です。
ただ、乱数やエントロピーなど他の概念の基礎として当然のように使用される非常に基本的な確率分布であるのでよく理解しておく必要がある。
ちなみに、一様分布であっても中心極限定理によって、標本の平均値は正規分布に近づくことが知られています。
第1章：臨床研究ではなぜ統計が必要なのか？計画することの重要性
第2章：研究目的をどれだけ明確にできるのかが重要
第3章：p値で結果が左右される時代は終わりました
第4章：多くの人が統計を苦手にする理由
第5章：統計を使えるようになるために今日から何をすれば良いか？
第6章：統計を学ぶために重要な環境
もしあなたがこれまでに、何とか統計をマスターしようと散々苦労し、何冊もの統計の本を読み、セミナーに参加してみたのに、それでも統計が苦手なら…
私からプレゼントする内容は、あなたがずっと待ちわびていたものです。
