EZRでT検定の詳細なやり方と解釈を簡単に説明！2群間の比較で用いられる検定

データを解析したことのある方なら、恐らく一度は目にしたことのあるT検定。

“統計と言えば平均値”というイメージがあるように、“統計学的検定＝T検定”というイメージを持っている方も少なくありません。

私も生まれて初めて統計学的検定を実施したのは、T検定でした。

＞＞T検定に関する概要を理解したい方はこちら。

 

今日の記事は、そんなT検定をEZRで実施する方法。

同じデータでT検定と分散分析（ANOVA）をしたら本当に結果は同じになるの！？というところまで解説します。

 

EZRでT検定を実施するために必要となるデータは？2群間の比較！

まずは、T検定を実施するために必要なデータを解説します。

T検定は、2群の母平均を検定する方法の1つでした。

 

ということは、用意するデータは以下の2つを満たす必要があります。

• 母平均を検定する方法であるため、目的変数には連続量のデータ（量的データ）が必要。
• 2群の群間で母平均を比較するので、2つ以上のカテゴリを持つ、カテゴリカルデータ（質的データ）が必要。

 

EZRでT検定をする今回の記事で使用するデータ：2群のデータ

ということで、今回の記事で使うデータです。

今回はA群、B群の2つの群で、LDHの平均値を比較してみます。

（データは架空のデータです。）

実際には、EZRで分散分析（ANOVA）を実施したデータに関してC群を削除し、A群とB群の2群だけのデータにしたものです。

 

 

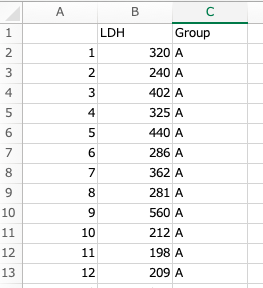
LDHが連続データで、Groupが群を示した変数です。

A群13例、B群11で、計24症例分のデータがあります。

 

EZRにT検定を実施する基となるデータを読み込む

ではここから、EZRにデータを取り込みます。

まずは、サンプルデータを適切な場所に保存しておきましょう。

 

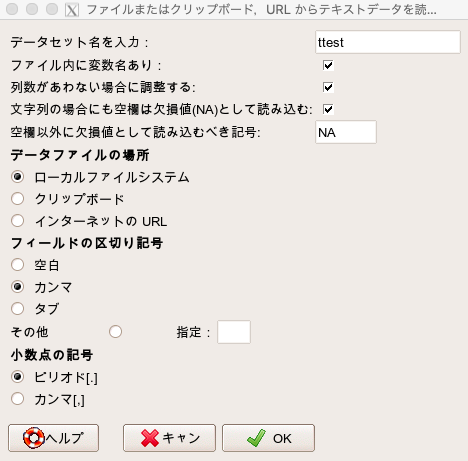
EZRを開き、「ファイル」→「データのインポート」→「ファイルまたはクリップボード, URLからテキストデータを読み込む」を選択します。

 

 

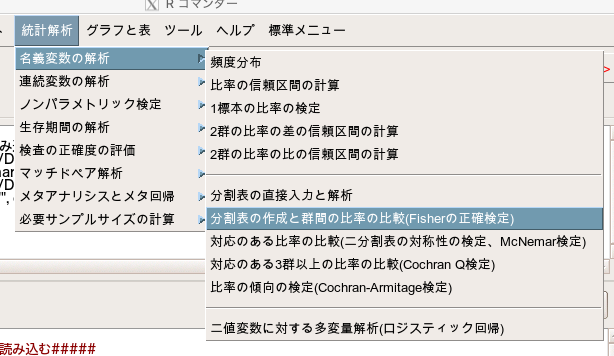
データセット名は「ttest」にしましょう（実際はなんでもよい）。

そして「ローカルファイルシステム」と「カンマ」にチェックを入れてOKを押します。

 

データセットが「ttest」になっていることを確認し、「表示」を押してデータが正しく表示されれば取り込み完了です。

 

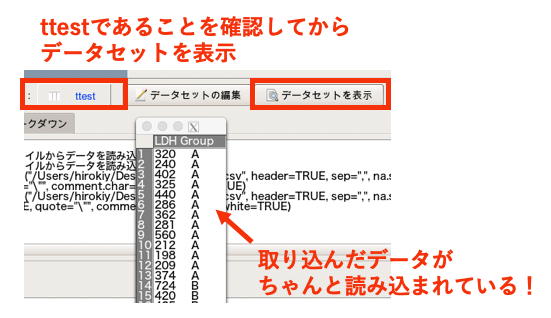
EZRでT検定を実践する！

解析するための準備が整いましたので、早速T検定を実施してみましょう。

T検定を実施するには、以下の手順で行います。

 

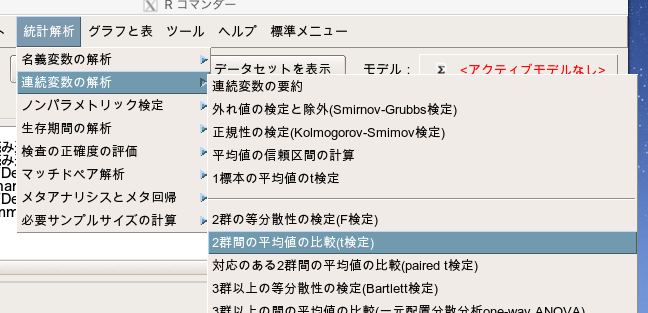
「統計解析」→「連続変数の解析」→「2群間の平均値の比較（t検定）」

 

 

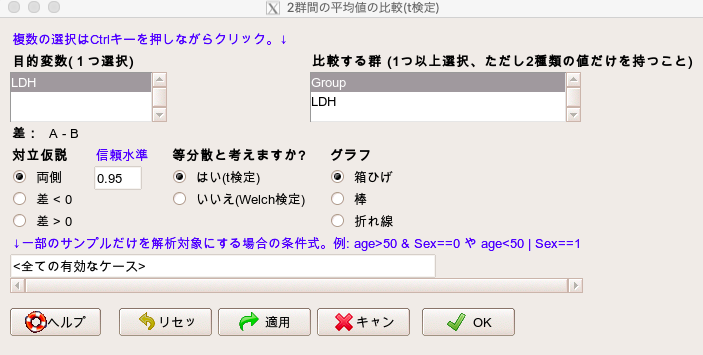
目的変数（1つ選択）で「LDH」を選択します。

比較する群（1つ以上選択）で「Group」を選択します。

グラフは「箱ひげ」を選択します。

等分散と考えますか？については「はい（t検定）」を選択します。

他は、いじらなくてOKです。

 

 

これで解析を実行すると、以下の解析を自動で行ってくれます。

• T検定の結果（P値や差の信頼区間などの結果を含む）
• 各群の平均と標準偏差の要約
• 各群の箱ひげ図の作成

 

EZRでのT検定結果の解釈をしよう

実際にT検定が実施できました。

では、結果の解釈をしていきましょう。

 

T検定の結果解釈

まずはT検定の解析結果です。

 

 

Data: LDH by factor(Group)とあります。

これは、GroupごとにLDHを比較したという意味です。

そして次の行にはt値、自由度、p値が表示されています。

 

自由度がなぜ22になるのかは理解できますか？

T検定の自由度は「データの数-群の数」だからですよね。

＞＞T検定での自由度がなぜ「データの数-群の数」になるのか！？

 

P値が0.05より小さいため、有意水準を0.05に設定していた場合には、有意差ありという結論になります。

＞＞有意水準、P値、有意差の関係を深く理解する！

 

次の行には対立仮説が表示されていますね。

T検定の帰無仮説は「2群の母平均に差がない」であり、対立仮説は「2群の母平均に差がある」です。

そのため対立仮説を言い換えると、「2群の母平均の差は0ではない」ということなので、結果に表示されている通りです。

＞＞帰無仮説と対立仮説の理解は検定をするうえで必須です！

 

その次には、2群間の差の95%信頼区間が表示されていますね。

95%信頼下限も上限もどちらもマイナスの値です。

つまり、0を含んでいないということ。

95%信頼区間が0を含んでいないことは、有意水準5%の検定結果が有意になることと同じ解釈ですので、ここからも有意差ありと分かります。

＞＞95%信頼区間と有意差の関係を理解する。

 

各群の平均と標準偏差の要約の結果解釈

その次に、各群の平均値と標準偏差が要約されています。

これはいいですよね。

平均値と標準偏差は、要約統計量の基本です。

 

EZRでT検定を実施すると箱ひげ図も出力される

設定の際に、グラフは「箱ひげ」を出力するようにチェックを入れたので、箱ひげ図が作成されています。

＞＞箱ひげ図に関して詳細に知る！

 

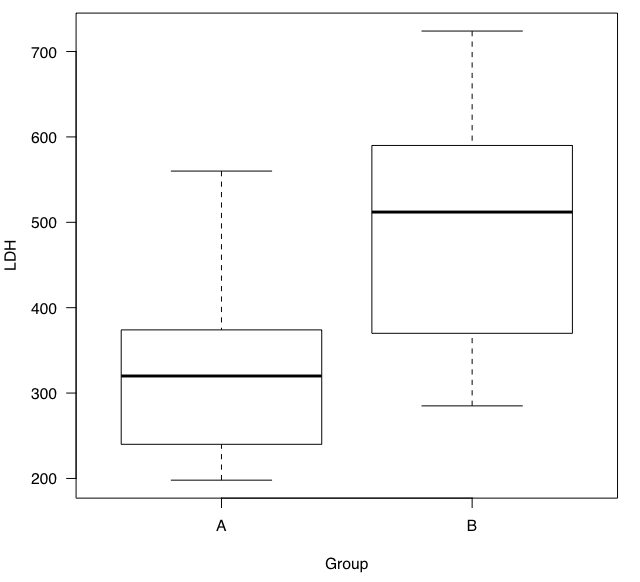
箱ひげ図は、箱の部分とひげの部分がある、かなり特徴的なグラフです。

箱が四分位範囲を示しています。

ひげは箱の1.5倍（それぞれ上側に1.5倍、下側に1.5倍の意味）の長さまでのデータの範囲を示しています。

ひげから外れたデータは、外れ値として示されています。

これを見るだけでも、データの分布がA群とB群で異なっていることが分かります。

 

2群間の比較で分散分析を実施するとどうなるのか？

分散分析に関する記事で、「ちょっとした知識」として掲載しておいた疑問。

2群のデータで分散分析を実施すると、T検定と同じ結果が出るって本当！？

ということを、実践してみます。

本当に同じ結果が出るのでしょうか？

それを検証するため、今回の2群のLDHのデータに対して分散分析を適用してみます。

 

分散分析をEZRで実施する手順としてはこちらの記事をご参照くださいね。

 

得られた結果がこちらです。

 

 

簡単のため、P値だけご紹介しますね。

すると、分散分析でP=0.00496が得られました。

これはT検定の結果と同じですね。

 

一応、T検定をした時の結果をもう一度貼り付けておきます。

 

ということで、2群のデータで分散分析を実施すると、本当にT検定と同じ結果が出力されました。

 

EZRでT検定を実施する方法まとめ

今回は、EZRでT検定を実施しました。

同じ2群のデータで分散分析をしても、T検定と同じ結果が出力されました。

 

こちらの内容は動画でもお伝えしていますので、併せてご確認くださいませ。