二項分布とは？わかりやすく正規分布との違いや近似できる問題も例を踏まえて

正規分布とともに、統計学ではよくでてくる二項分布。

二項分布はコイントスでのコインの表と裏のように、結果が2つしかないときに生じる分布です。

この記事では、二項分布に欠かせないベルヌーイ試行と二項分布について、正規分布との違いも含めて統計初心者にもわかりやすく説明していきます。

 

二項分布とは？ベルヌーイ試行との関係

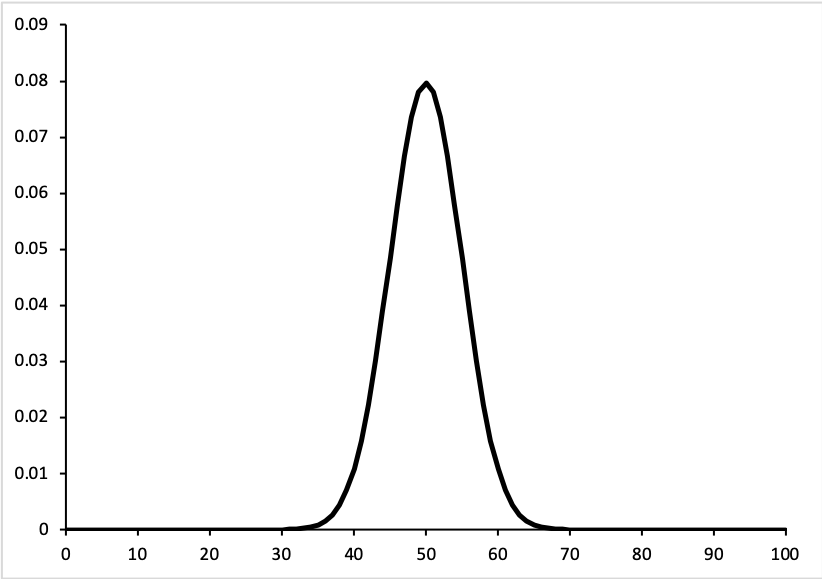
上の図は、コイントスを100回行ったときに、コインが表になる回数になる確率を表したものです。

コイントスのように、ある行動や試行に対して結果が2つしかないときに生じる分布を、二項分布と呼びます。

“ある行動や試行に対して結果が2つしかない”ということが、二項分布では重要になります。

 

二項分布はベルヌーイ試行の確率分布：”試行に対して結果が2つしかない”

“試行に対して結果が2つしかない”ような実験や試行のことをベルヌーイ試行と言います。

二項分布はベルヌーイ試行の確率分布です。

 

例えば「勝ちと負け」、「生と死」、「アタリとハズレ」、「表と裏」といったものです。

 

このベルヌーイ試行であるには3つの条件があてはまる必要があります。

1. 試行の結果は成功か失敗かどちらかであること。
2. 各試行は独立であること。
3. 成功確率と失敗確率は常に一定であること。

 

ベルヌーイ試行では結果が2つしかないので、

成功確率 =   1 – 失敗確率

という関係が成り立ちます。

また、成功確率はp、失敗確率はqとしても表されることがよくあります。

 

では、これら3つの条件を順番に解説していきます。

 

ベルヌーイ試行の条件1：”試行の結果は成功か失敗かどちらかであること”

これは、例えばコイントスの場合、コインの表=成功、コインの裏=失敗として考えてみます。

するとコイントスも、“試行の結果は成功か失敗かどちらかであること”の条件に当てはまります。

 

しかし、もしコインが割れたり、コインがたったりして、表と裏以外の結果が存在する場合は、”試行の結果は成功か失敗かどちらかであること”にあてはまらず、ベルヌーイ試行ではないと言えます。

 

ベルヌーイ試行の条件2：”各試行は独立であること”

コイントスでは、1回投げて表が出たとしても、次のコイントスでは表と裏が1：１の確率で出ます。

このように、前の試行の結果が次の試行に影響与えないことを”各試行は独立”と言います。

 

一方で、くじ引きで、10本のくじの中で1本のあたりがあるときを考えてみます。

10本のくじの中で1本のあたりがあるので、あたりを引く確率は1/10ですよね。

しかし、もし一人目の人があたりのくじを引いてしまうと、二人目の人があたりを引く確率は0/9となってしまいます。

このように、前の試行がそれ以降の試行の結果に影響を与える場合は、”各試行は独立”ではないので、ベルヌーイ試行ではないと言えます。

 

ベルヌーイ試行の条件3：”成功確率と失敗確率は常に一定であること”

サイコロを投げる時、6の目が出る確率（成功）と、6の目が出ない確率（失敗）は1/6：5/6の確率で出ます。

これは“成功確率と失敗確率は常に一定”であると言えます。

 

しかし、もしサイコロ投げが上達して6の目を出すコツをつかんだとしたら、6の目が出る確率が増加して、6の目以外が出る確率が減少していくでしょう。

これは“成功確率と失敗確率は常に一定”ではなので、ベルヌーイ試行とは呼べません。

 

二項分布とは？わかりやすく！

二項分布は、先ほど説明したベルヌーイ試行の確率分布です。

二項分布では試行回数をn、成功した回数をk、成功する確率をpの文字でよく表します。

 

式で書くと下のようです。

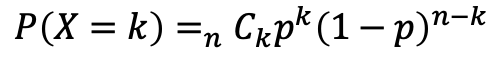
ややこしいですね。

この式を覚える必要はないです！！

 

しかし、覚えていてほしいこともあります。

それは、二項分布では、試行回数n、成功した回数k、成功する確率pがあれば、期待値（平均）と分散が簡単に計算することができるということ。

 

二項分布の期待値（平均）

二項分布の期待値は

二項分布の期待値 = 試行回数 x 成功する確率 = n x p

です。

すごい簡単ですよね。

 

二項分布の分散

二項分布の分散は

二項分布の分散 = 試行回数 x 成功する確率 x (1 – 成功する確率)

文字式で表すと、

二項分布の分散 = n x p x (1 – p)

です。

これも、すごい簡単ですよね。

 

二項分布と正規分布の関係は？どこに違いがあるの？

二項分布と正規分布にはおもしろい関係があります。

それは、二項分布の期待値（平均）と分散はnが大きくなると、正規分布で近似できるというものです。

 

先ほど、

二項分布の期待値  = n x p

二項分布の分散 = n x p x (1 – p)

という式を紹介しました。

 

この関係式によると、期待値（平均）と分散の両方の式に、試行回数nが入っています。

つまり、試行回数nを大きくすれば、期待値と分散は正規分布に近似することができます。

 

正規分布を導出するメリットは、2つあります。

1. 正規分布は標準偏差がわかれば、ある範囲にデータが含まれる確率がわかる
2. 標準正規分布表を使えば、ややこしい計算が必要なくなる

という点ですね。

正規分布とは？簡単にわかりやすく標準偏差との関係やエクセルでのグラフ化を解説

標準正規分布表の見方について！標準化やZ値の計算式はどうすればいい？

 

詳しい導出は省きますが、正規分布に近似した二項分布の標準偏差は

次の式で表すことができます。

標準偏差 = sqrt[（p(1 – p)/ n）]

 

この性質は、世論調査や視聴率の調査などで利用されています。

標準偏差と標準誤差の違いをわかりやすく！グラフでの使い方とサンプル数についても

 

二項分布に関するまとめ

• 行動に対して結果が2つしかない試行のことをベルヌーイ試行と呼ぶ
• 二項分布はベルヌーイ試行の確率分布
• 試行回数nを大きくすればに二項分布の期待値と分散は正規分布に近似できる