主成分分析（PCA）とは？手順や用語の解説を含めてわかりやすく解説！

本記事では「主成分分析（PCA）とは？手順や用語の解説を含めてわかりやすく解説！」ということでお伝えします。

主成分分析はprincipal component analysis; PCAとも呼ばれ、独特の用語を使っていたりするので、なかなかイメージが湧きにくいかもしれません。

そのため本記事では

• 主成分分析とはそもそも何か？目的は？
• 主成分分析を実施する際の手順を整理
• 主成分分析の用語を解説

ということでお伝えしていきます！

主成分分析（PCA）とは？例を用いて解説

主成分分析を一言で言うと「多くの変数の情報をできるだけ損なわずに、少数の変数に縮小させることを目的とした解析手法」ということ。

例えば、体重と身長という2つの変数がある場合に、BMIという1つの変数に縮小させる、というようなイメージを持っていただければOK。

時には100以上の変数がある研究でも、2つ・3つの変数にできれば可視化も簡単になります。

主成分分析自体は「少数の変数に縮小させる」という目的だけであり、縮小させた変数をどう使うかはまた別問題

主成分分析の注意点としては、主成分分析自体は「少数の変数に縮小させる」という目的だけであり、縮小させた変数をどう使うかはまた別問題である、ということ。

そのため、主成分分析をした後に何を知りたいのか？という目的が明確ではないと、主成分分析をした後の結果の解釈ができなくなります。

主成分分析をした後に、縮小された変数を用いて回帰分析を行う、などがアイデアとして挙げられますね。

主成分分析によって得られた主成分は互いに独立なので、縮小された変数を用いた回帰分析では、多重共線性を気にしなくて済む、というメリットもあります。

ただし、縮小された変数（主成分）がどのような意味を持つかは自分で考える必要があるため、結果の解釈が難しいという点は残ります。

主成分分析のメリットデメリットをまとめてみる

ここまで主成分分析の特徴などをお伝えしました。

では主成分分析のメリットデメリットを一度まとめてみます。

主成分分析のメリット

主成分分析のメリットは1つです。

1. データ数（変数の数）を少なくして、その後の可視化や回帰分析を容易にすることができる

これが主成分分析を用いるメリット。

変数の数が多くなればなるほど、回帰分析を行う際の説明変数をどう選択するか？といった問題が出てきます。

しかし主成分分析をすれば、変数の数が2つや3つ程度に抑えることができますので、説明変数をどう選択するか？という問題は無くなりますね。

主成分分析のデメリット

では、主成分分析のデメリットは何があるでしょうか。

デメリットは主に2つあります。

1. 主成分分析を実施する前の情報量よりは情報量が落ちる
2. 分析結果は研究者の判断に委ねられる

まずは、元の情報量よりは情報量が落ちます。

変数を少なくするので当たり前ではあるのですが、一応デメリットですね。

そしてもう一つは分析結果は研究者の判断に委ねられる、という点。

私の中では、この「分析結果は研究者の判断に委ねられる」という点が一番のデメリットかなと思います。

研究はデータを解析するだけで終わることはなくて、その結果を解釈して考察までして初めて完了します。

そのため、結果の解釈が難しい解析は極力避けるべきではないかなと思っています。

主成分分析の手順

では、主成分分析を実施する際にはどのような手順で実施すればいいのでしょうか。

大きく分けて3つのステップがあります。

1. なぜ主成分分析をするのか、目的を明確にする
2. データを解析できる状況にする
3. 統計ソフトで解析する

それぞれ詳しくみていきましょう。

主成分分析の手順1：なぜ主成分分析をするのか、目的を明確にする

ここがめちゃめちゃ重要です。

前述の通り、主成分分析をしただけでは変数を縮小することにしかなりません。

主成分分析した後の変数をどう解釈し、そしてどう使うか。

そのようなことをハッキリさせておかないと、主成分分析をやりました、だけで終わってしまいます。

そのため、主成分分析をすることで研究のどんな目的を解決できるか明確にする必要がありますね。

主成分分析の手順2：データを解析できる状況にする

主成分分析を使う目的がはっきりしたら、データを解析できる状況にします。

具体的には、単位が違うものを主成分分析する場合、標準化しておく必要がある、ということ。

標準化とは、データを平均0、分散（標準偏差）1にするということです。

標準化自体は簡単で、各データの値に対して「（データの値-平均値）/標準偏差」という計算をすればいいだけ。

主成分分析の手順3：統計ソフトで解析する

最後に、統計ソフトで解析すれば完了です。

無料で使えるEZRでも主成分分析が可能です。

下記の通り、「標準メニュー」→「統計量」→「次元解析」→「主成分分析」で実施できます。

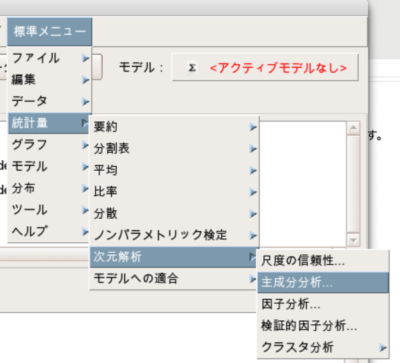
実際にEZRでどう解析するのかは、別記事で紹介させていただきますね。

主成分分析の用語解説：寄与率や固有値などはどんな意味？

主成分分析には独特の用語が多く使われているのも特徴的ですね。

そのため、用語を整理しておきましょう。

具体的には以下の7つを簡単に整理します。

1. 主成分
2. 主成分得点
3. データの標準化
4. 固有値
5. 固有ベクトル
6. 寄与率
7. 累積寄与率

主成分分析の用語1：主成分

主成分とは、分析対象の各変数を統合して作られた、縮小した変数のことです。

第一主成分、第二主成分、、、、という感じで呼ばれます。

主成分分析の用語2：主成分得点

例えば元の変数が5つの場合、主成分は以下のように表現されます。

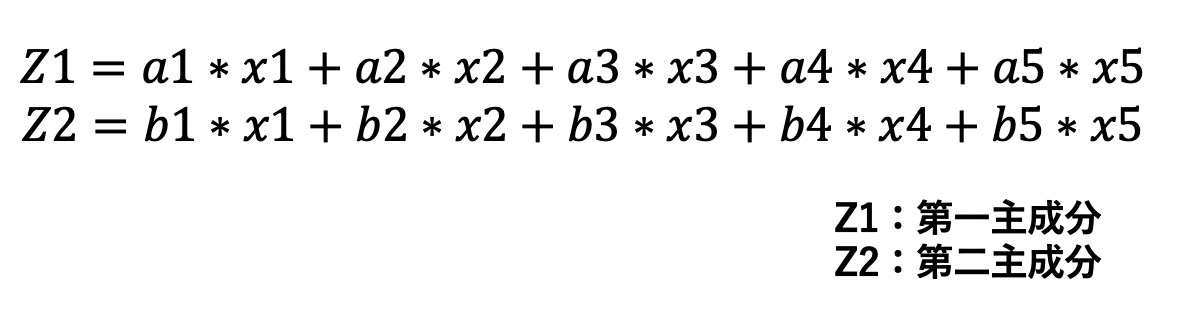
この関係式に代入して求めた値のことを、主成分得点と呼んでいます。

EZRで計算すると、データセットに主成分得点を保存することができます。

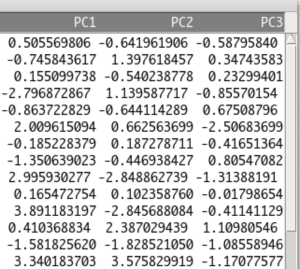
PC1が第一主成分得点、PC2が第二主成分得点、PC3が第三主成分得点、ということですね。

主成分分析の用語3：データの標準化

前述していますが、単位が違うものを主成分分析する場合、標準化しておく必要があります。

標準化とは、データを平均0、分散（標準偏差）1にするということ。

標準化自体は簡単で、各データの値に対して「（データの値-平均値）/標準偏差」という計算をすればいいだけ。

主成分分析の用語4：固有値

固有値とは、主成分の分散のことを指します。

EZRでは「Component Variance」という名称で出力されます。

主成分分析の用語5：固有ベクトル

固有ベクトルとは、以下の関係式での回帰係数のことを指します。

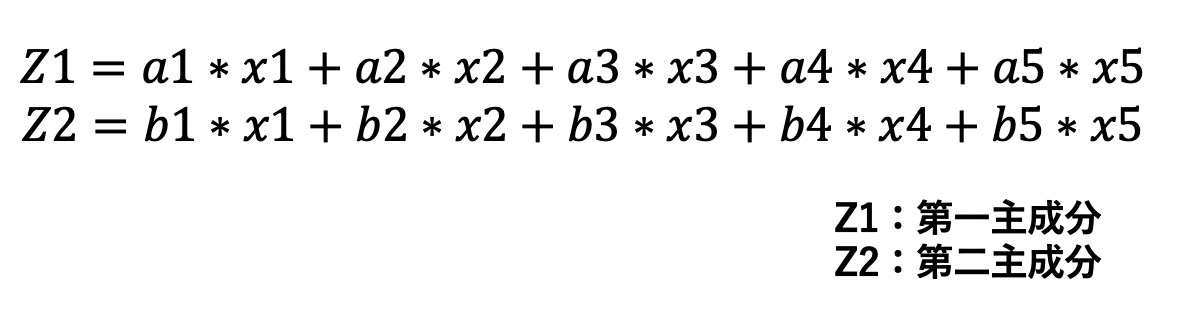
つまり、a1,a2,a3,a4,a5、b1,b2,b3,b4,b5のことを固有ベクトル、と呼んでいます。

主成分分析の用語6：寄与率

寄与率とは、対象とする主成分に、元データの情報がどれだけ反映されているかを表した数値のことです。

例えば第一主成分の寄与率が0.5である場合、第一主成分に元のデータの50%が反映されている、ということを意味します。

主成分分析の用語7：累積寄与率

第一主成分、第二主成分…の寄与率を足し合わせたものを累積寄与率と呼びます。

第一主成分の寄与率が0.5、第二主成分の寄与率が0.25の場合、第二主成分までの累積寄与率は0.75になります。

まとめ

いかがでしたか？

本記事では「主成分分析（PCA）とは？手順や用語の解説を含めてわかりやすく解説！」と言うことでお伝えしました。

• 主成分分析とはそもそも何か？目的は？
• 主成分分析を実施する際の手順を整理
• 主成分分析の用語を解説

ということが理解できたのなら幸いです！！