統計でよく用いる手法である、対数変換。
対数変換はどんな手法なのでしょうか?
また、統計で対数変換が必要になるのはなぜでしょうか?
この記事では、統計で用いる対数変換の手法や対数正規分布についてわかりやすく説明していきます。
対数変換とは?

対数変換とは、ズバリ「データに対して対数をとること」です!
対数は数学で習ったlogまたは、lnです。
例えば、
10、100、1000といった値を基底10の対数を取れば、それぞれ
log10=1、log100=2、log1000=3と、対数変換をすることができます。
ここまでは、数学で習う対数の計算ですね。
ではなぜ、統計学で対数変換が必要になるのでしょうか?
それは前提として、対数正規分布(右に裾を引く分布)の知識が重要になりますので、対数正規分布について解説します。
対数正規分布(右に裾を引く分布)とは?

統計学では正規分布が非常に重要であることは他の記事でも解説してきました。
>正規分布とは?簡単にわかりやすく標準偏差との関係もガウス分布に関して解説
>標準正規分布表の見方や使い方!標準化とZ値の計算式やマイナスの時は?
対数変換が統計学においても重要になるのは、対数変換すると正規分布になる、対数正規分布が存在するからです。
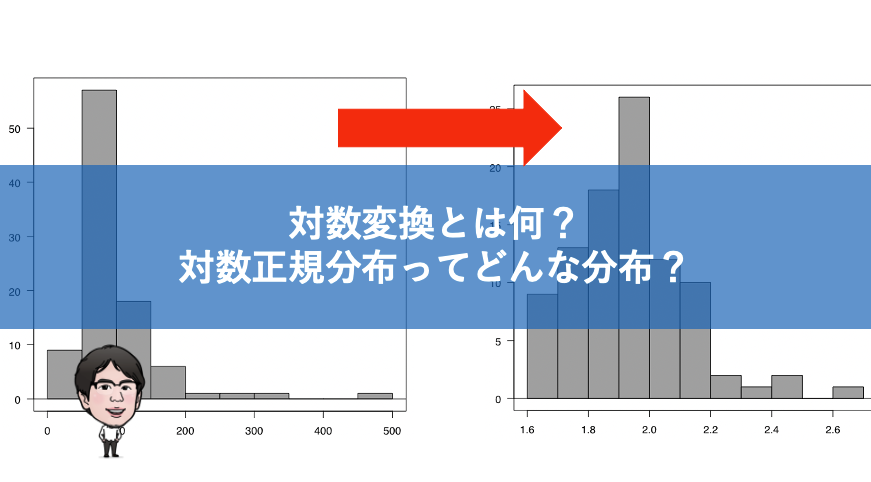
こちらが、対数正規分布の例。(あまりきれいな対数正規分布ではないですが。。)
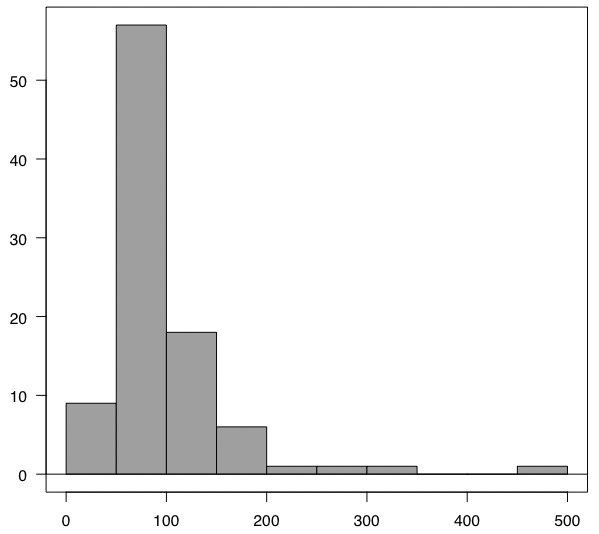
対数正規分布は、左側から最頻値にかけて急激に上昇し、右に行くに連れてなだらかになるという特徴があります。
右側の裾がなだらかなので、対数正規分布は「右に裾を引く分布」とも呼ばれています。
医学系のデータですと、生化学データや薬物動体データの多くが、対数正規分布に従うことが知られています。
対数正規分布を対数変換すると正規分布に近づく
なぜ対数変換に対して対数正規分布が重要かと言うと、対数正規分布を対数変換すると正規分布に近づく、という性質があるからです。
先程の対数正規分布のヒストグラムを対数変換すると、下記のようなヒストグラムになります。
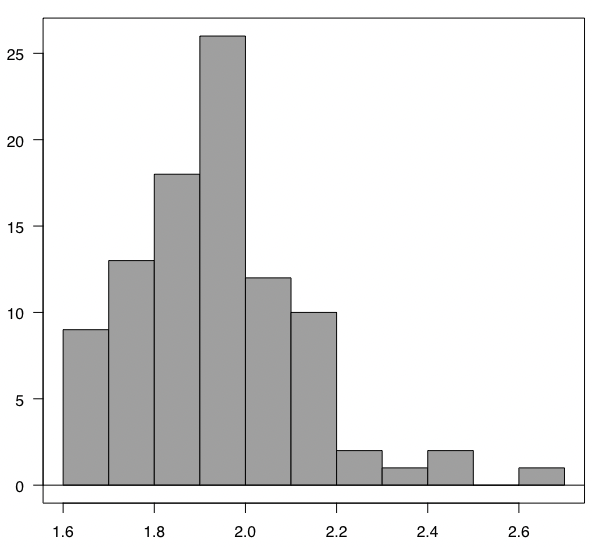
実際のデータなので綺麗な正規分布とは言わないまでも、少なくとも対数変換前よりも正規分布に近づいていることがわかります。
そして正規分布に変換できると、あとはこれまで見てきた正規分布に用いることができる様々な手法(パラメトリックな手法)を用いることができるので、非常に便利です。
対数正規分布のデータを対数変換すると、正規分布に近づく。それによって、正規分布を仮定した解析手法(パラメトリックな手法)を適用することができる。
これが統計における対数変換が重要な理由です。
0の値の対数変換はどうするの?
定義上、値が0の場合は、対数をとることができません。
つまり、ゼロを含むデータでは対数変換を行うことはできません。
ではどうすれば良いのでしょうか?
それはデータの値全てに1を足すです。
すると0+1=1で対数をとることができるようになります。
ただ、足す数字が”1″である必要はありません。
実際、データの連続性を考慮したとき0.5を足すのが良いという議論もあります。
話をまとめると、0を含むデータを対数変換するときは、
一定の値をデータに足すことで、0をデータから無くすという操作を行います。
特に理由がなければ”データに1を足す”で問題ないです!
対数変換と幾何平均の関係

次に、対数変換と幾何平均の関係についてお伝えします。
一口に「平均」といっても、実は数種類の平均があることをご存知でしょうか??
- 算術平均
- 幾何平均
- 調和平均
この3つが有名ですが、何の断りもなく「平均」とあれば、それはほとんどの場合、算術平均を示します。
算術平均は、あなたもご存知の通り「全てのデータを足す/データの数」で求めることができる平均値です。
では一方で、幾何平均とはなんでしょうか。
幾何平均は「全てのデータをかけて累乗根を取る」というのが幾何平均です。

じゃあなぜ対数変換と幾何平均が関わっているのか?というと、対数変換したデータに対して算術平均を計算すると、それは、「対数変換前の幾何平均を対数変換したもの」だからです。
例を見てみましょう。
AとBの2つのデータに対して、対数変換したlogA, logBがあったとします。
対数変換した後のlogAとlogBの算術平均は
(logA+logB)/2 = (logA*B)/2 = logA*B1/2
となって、まさに「対数変換前のデータAとBの幾何平均を対数変換したもの」になっていますよね。
逆に言えば、対数変換したデータの算術平均を指数変換すれば、幾何平均になります。
さらに言えば、対数変換したデータの算術平均の2群の差は、指数変換すると幾何平均の比になります。
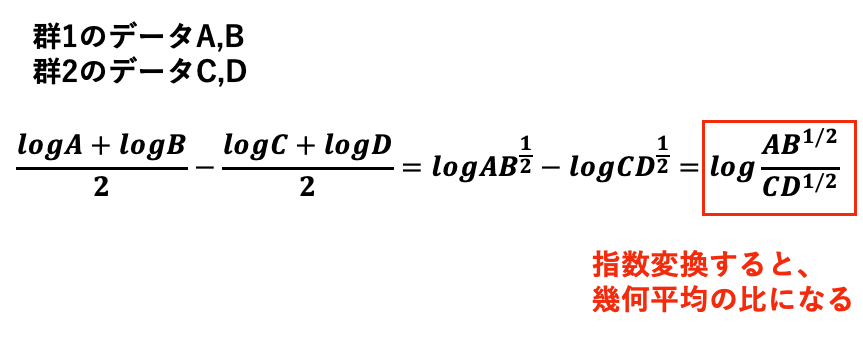
なので、対数変換時か平均は密接な関係があるのです。
対数変換して解析した際に論文や学会ではどう報告するのか?

対数変換は、対数正規分布(右に裾を引く分布)を正規分布に近づけるために用いられる方法だということがわかりました。
さらに、対数変換した後に算術平均を出すことは、元データに対して幾何平均を計算していることだということもわかりましたね。
なので、対数変換したデータを実際に論文や学会報告をするときには2通りの報告の仕方があることがわかります。
- 対数変換後のデータの算術平均の差を提示する方法
- 対数変換後のデータの算術平均に対して指数変換した後の、幾何平均比を提示する方法
どちらを示せばいいのか?ということに対して、「こっちが絶対にいい!」という答えはありません。
ですが、トップジャーナルであるNEJMでは、「どちらの結果も提示している」論文がありました。
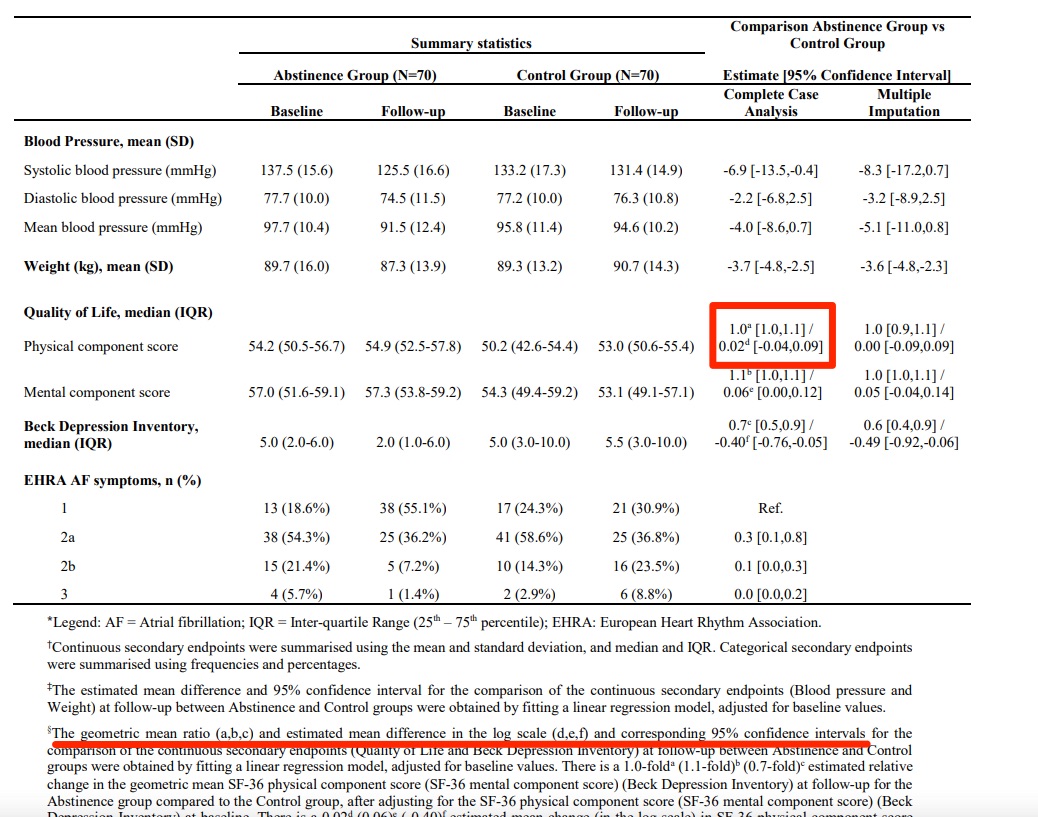
なので、どちらの結果を提示してもいいと思いますし、編集者や査読者から指摘があったら、その指示に従えばいいですね。
まとめ

対数変換することの重要性はわかりましたでしょうか?
データに対して変換するほど、正規分布は統計学の中でかなり重要な分布であることもわかりましたね。
そして、対数変換と幾何平均の関係も学びました。
ぜひ対数変換・正規分布・幾何平均の関係をイメージできるように繰り返し学んでいきましょう!!
統計に関するご質問があれば、メルマガにご登録の上ご質問くださいませ!













コメント