ポアソン分布とは？わかりやすく簡単に例を用いて二項分布との関係も

正規分布や二項分布、カイ二乗分布の他に、統計学でよく出てくる分布にポアソン分布が存在します。

ポアソン分布は、「ランダムに起きる事象」がある期間に何回起こるかの確率を調べるときに用いる分布です。

ポアソン分布とはどのような分布なのでしょうか。

この記事ではポアソン分布について簡単にわかりやすく説明していきます。

 

ポアソン分布とは？わかりやすく解説！

ポアソン分布は、ある事象がある期間に生じる確率を表す分布です。

 

例えばある県内で、自転車事故が一日あたり、人口10万人あたり5件発生したとます。

では、人口10万人あたり1年間で生じる自転車事故の確率は、どうなるでしょうか。

 

このような問題はある”事象”を考えます。

上記の例で事象とは、「事故が生じるか生じないか」ということ。

 

このような考え方は、以前にも出てきました。

コインの表と裏のような物事を表す分布、二項分布でしたね。

 

ポアソン分布の事象はコインの表と裏のように、ある事象が起こるか、起こらないかの２通りあるで考えることができます。

そのため、ポアソン分布の基本となののは、二項分布の考え方です。

 

>>>二項分布とは？初心者にもわかりやすく正規分布に近似できる問題も解説

 

二項分布について、非常に簡単におさらいしていきます。

 

ポアソン分布を理解するための復習: 二項分布

二項分布はコインの表と裏のように2通りの結果が生じる事象を繰り返して行なったときの分布でしたね。

2通りの結果が生じる事象を繰り返して行うことをベルヌーイ試行と呼びます。

 

ここで一番、思い出して欲しいのは、

二項分布では期待値（平均）はとても簡単に計算できることです。

二項分布の期待値は

二項分布の期待値 = 試行回数 x 成功する確率 = n x p

でした。

 

>>>二項分布とは？初心者にもわかりやすく正規分布に近似できる問題も解説

 

先ほどの自転車事故の例では、

人口10万人あたりの一年間の事故の発生確率の期待値

=365日 x 人口10万人あたりの一日の事故の発生確率

と同じように求めることができます。

*ただし、冬場は事故が多いなどは無視して、1年中同じ確率で事故が発生すると仮定しています。

 

二項分布の分散は

二項分布の分散 = n x p x (1 − p)

でしたね。

この考え方がポアソン分布でも用いることができます。

 

ポアソン分布は二項分布の極限！λは何を意味する？

では、ポアソン分布の確率関数P(k)はどのようにして求めることができるのでしょうか。

実は、ポアソン分布は二項分布の極限として求めることができるのです。

単位時間あたり平均λ回起こる事象が、単位時間あたりk回発生し、この確率をP(k)とする。

具体的に数式を用いて計算すると以下のようになります。

ちなみにeはネイピア数または自然対数の底と呼ばれる定数で、e=2.718281828459045235360287471352・・・と無限に続く値。

ネイピア数を含む上の算式がポアソン分布の確率関数の具体的な算式です。

λが0.1、1.5、5の場合のポアソン分布のグラフを作るとこんな感じ。

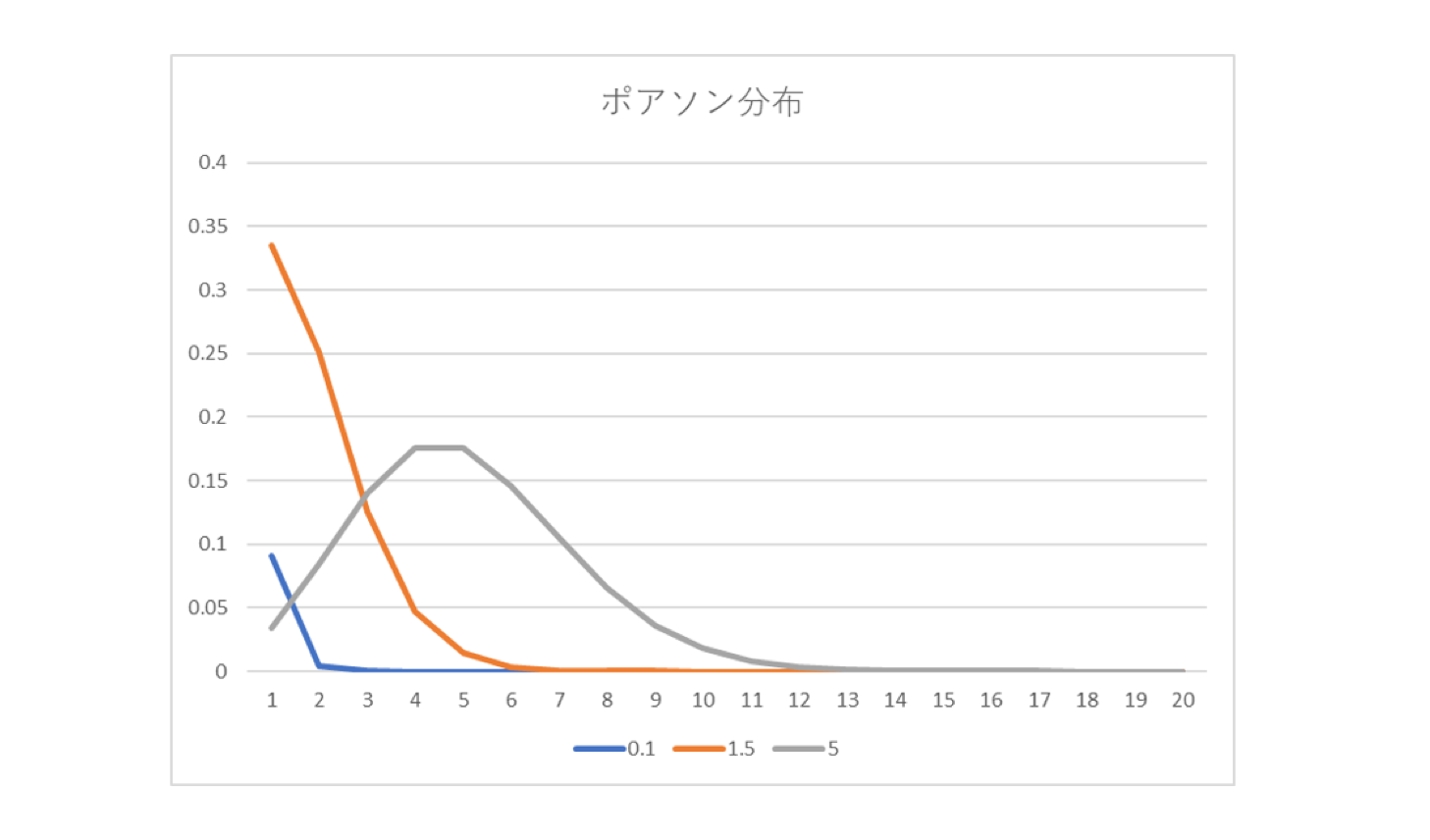
このグラフから分かることは、

１．λが大きいと右にシフトする

２．λが小さいと急激に下がって0近くにへばりつく

 

例えば、上のポアソン分布が1日あたり交通事故の発生回数の分布だとしましょう。

 

不思議なことに上のグラフの3例の中では、1日あたり交通事故の発生回数が平均1.5回のポアソン分布にしたがう場合において、1日に2回交通事故の発生する確率が一番高くなった。

要するに平均と近い回数の確率が高くなる傾向にあるということ。

ポアソン分布にしたがう現象の確率の求め方がお分かりになりましたか。

もっと平均を細かく動かしてポアソン分布のグラフを書いてみたらいろいろな傾向がつかめて理解が深まるかも。

 

ポアソン分布をエクセルで確認してみよう

例えばマイクロソフトのエクセルでポアソンの確率関数を計算するには、POISSON.DIST(回数,平均,FALSE)という関数を使えば簡単に求められます。

時間がある方は是非やってみてください。

確率関数の形も、ネイピア数のマイナスλ乗とλのk乗の積をkの階乗で割っただけのものですから、簡単に計算できますよね。

簡単な割にいろいろな現実の問題に適用できて便利なのです。

ポアソン分布が適用できるデータの例は？

ポアソン分布は、ある事象の起こりやすさがランダムで生じると仮定したときに、

「単位時間あたり平均λ回生じる事象が、単位時間にk回生じる確率」を表すのに用いる確率分布です。

 

先ほどの自転車事故の例では、

人口10万人あたりの一年間の事故の発生確率の期待値（λ）

=365日 (n) x 人口10万人あたりの一日の事故の発生確率 (p)

となります。

 

上の例のように、nが大きく、pが小さいときλは一定と考えることができます。

1年あたり車の通る台数（n）はかなり大きいですが、事故の発生確率（p）は小さいですからね。

このとき、ある期間でλ回発生する事象が、一定時間に回数k発生する確率がポアソン分布となります。

 

つまり、ポアソン分布はこのようにいうことができます。

 

ポアソン分布の性質

次にポアソン分布の性質を説明していきます。

ポアソン分布も元は二項分布でしたよね。

そのため、k回生じたのkは整数の値をとります。

 

また、次に2つの性質があります。

• ポアソン分布の期待値（平均）はλ
• ポアソン分布の分散はλ

少しユニークですね。

 

期待値がλになるのは先ほど見た通りです。

分散がλになるのは、二項分布の分散、

二項分布の分散 = n x p x (1 − p)

から、考えることができます。

ポアソン分布の条件であるpが十分に小さいとき、

(1 − p) 〜 1

になります。

そのため、

ポアソン分布の分散 = n x p x (1 − p)　= n x p x 1 = n x p =　λ

となります。

 

さらに、ポアソン分布の最頻値はλ以下の最大の整数となります。

これは、λは整数以外の値をとるためです。

もし、λが整数ならλが最頻値をとります。

 

ポアソン分布と間違え注意: ピアソン

ポアソン分布とよく似た語幹の用語に、ピアソンがあります。

ピアソンは、ピアソンの相関係数でよく出てきます。

>>>相関係数とは？p値や有意差をどう解釈すれば良いのかわかりやすく！

たまに、ピアソンとポアソンを混乱することがあるので、気をつけましょう。

 

ポアソン分布はどのようなときに使うのか？

ポアソン分布はどのようなときに出てくるのかを考えていきます。

ポアソン分布の例でよく出てくるのは、不運にも事故に遭遇する回数です。

また、病気に疾患する確率や、不良品の割合など、世の中で発生する様々な事象に用いられています。

そのため、とても実用的な分布です。

 

ポアソン分布の期待値（平均）と分散はどうなっている？

ポアソン分布の期待値(平均値)を求めるために、まず、期待値(expctation)というものについて理解しましょう。

ポアソン分布のような確率関数が離散的であるような確率分布の期待値は、確率変数と確率関数の積について定義域に亘って和をとったもののことです。

確率変数の分布を端的に示す指標といえる。

 

ところがポアソン分布の期待値は、上のような和の計算を行わなくても、実は定義から直感的に求めることができます。

どういうことかと言うと、ポアソン分布とは平均してλ回ランダムに起こる事象が、単位時間にちょうどk回起きる確率の分布のことなので、λが期待値ということ。

 

次に、分散について理解しましょう。

期待値だけでは、ある確率分布がどのくらいの広がりをもって分布しているのかがわからない。

そこで、平均の周りにどの程度分布するかの指標として分散 (variance) がある。

平均と合わせると、確率分布を測定するときの良い指標となる。

確率関数が離散的であるような確率分布の分散は、確率変数と平均との差の2乗と確率関数の積ついて定義域に亘って和をとったもののことです。

ただ、上の定義式のまま分散を計算しようとすると、かなりの計算量となる場合が多いので、分散の定義式を変形して、以下のような式にしてから分散を求める方が多少計算が楽になる。

分散＝確率変数の2乗の平均－確率変数の平均の2乗

ポアソン分布の分散は、直感的には求まりませんが、上の定義に従って計算すると分散は期待値と同じλになります。

すなわち、ポアソン分布の場合、イベントの平均的な発生回数λだけ、平均からぶれるということ。

 

ポアソン分布の期待値（平均）と分散の求め方・証明は？

ポアソン分布の期待値（平均）は、「確率変数と確率関数の積ついて定義域に亘って和をとったものの」という定義式に沿ってとにかくひたすら計算すると求まります。

では実際に計算してみましょう。

ポアソン分布の期待値（平均）は、

上のような式変形だけで結構あっさり計算できる。

次に、ポアソン分布の分散は、確率変数と平均との差の2乗と確率関数の積積ついて定義域に亘って和をとったもののですが、「ポアソン分布の期待値（平均）と分散はどうなっている？」で説明した必殺技

分散＝確率変数の2乗の平均－確率変数の平均の2乗

を使って求めることにします。

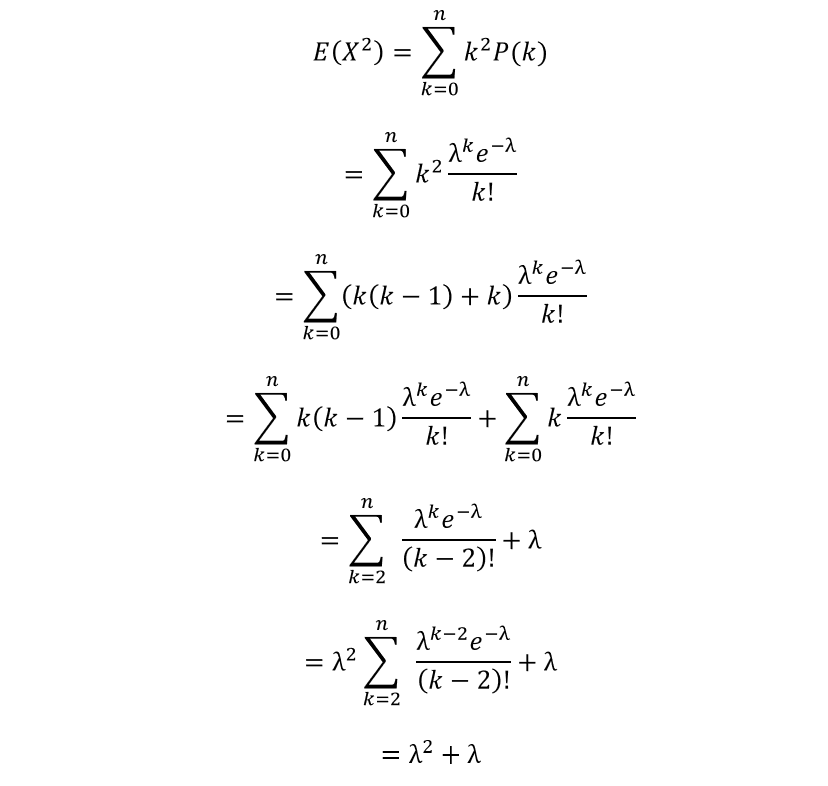
よって、ポアソン分布の分散は

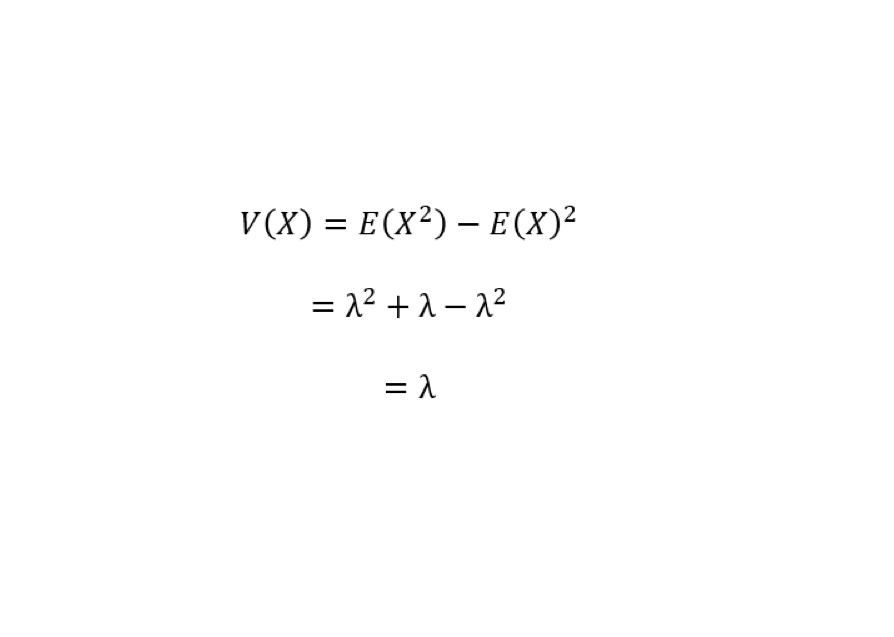
と、平均も分散もλとなりました。

これはシンプルで覚えやすい。

ポアソン分布の平均も分散も高校数学レベルの和の計算をひたすら繰り返すことで求めることが出来ることがお分かりいただけたでしょうか。

 

ポアソン分布に関してまとめ

• ポアソン分布は、「単位時間あたり平均λ回生じる事象が、単位時間にk回生じる確率」をあらわっす
• ポアソン分布の基本は二項分布の考え方
• 二項分布でnが大きく、pが小さいときλは一定と考えることができ、このときポアソン分布に従う
• ポアソン分布の期待値はλ
• ポアソン分布の分散はλ