この記事では「JMPでカイ二乗検定とフィッシャーの正確確率検定を実施！クロス集計表の検定」としてお伝えします。
「カイ二乗分布」と、「フィッシャーの正確確率検定」は分割表（クロス集計表）の検定などで大活躍する検定方法です。
この記事では、統計解析ソフトJMPを用いてクロス集計表の検定である、カイ二乗検定とフィッシャーの正確確率検定の方法について解説していきます。
Contents
クロス集計表の検定では「カイ二乗分布」と「フィッシャーの正確確率検定」はどちらを使う?
クロス集計表の検定として、「カイ二乗分布」と「フィッシャーの正確確率検定」はどちらも同じ目的で利用されますが、検定のため計算方法が異なります。
そのため、検定結果も少し異なってきます。
一般的には、p値の算出が単純である「カイ二乗分布」を用いたらいいです。
>>>カイ二乗検定とは？計算式まで簡単に分かりやすく！分割表の検定
「フィッシャーの正確確率検定」は近似を用いません。
標本サイズが小さい場合や、度数が0のセルがある場合などに適しています。
詳しくは
>>>フィッシャーの正確確率検定とは？カイ二乗検定と何が違う？分割表の検定
>>相対度数とは？度数分布表からの求め方をわかりやすく！パーセント表示がいい？
で解説しています。
JMPでカイ二乗検定を実施する！
では、JMPでカイ二乗検定の使い方を見ていきましょう！！
カイ二乗検定はクロス集計表に対する独立性の検定
クロス集計表に対してカイ二乗検定は主に独立性の検定に用います。
独立性の検定は、二つの変数に関連が言えるのか否かを判断するためのものです。
この独立性の検定は分割表を用いるときによく用います!
>>>カイ二乗検定とは？計算式まで簡単に分かりやすく！分割表の検定
カイ二乗検定するためのJMPへのデータの読み込み
自分たちのデータを解析する場合は、
[ファイル] > [開く]から解析したデータを開いてください。
ExcelやCSV形式のデータを開くことができます。
この記事では、JMPにすでに用意されているサンプルデータを使います。
[ヘルプ] > [サンプルライブラリー]をクリックします。
すると、次のサンプルデータのディレクトリのウィンドウが出てきます。
今回はこの中の” Consumer Preference.jmp”を使います。
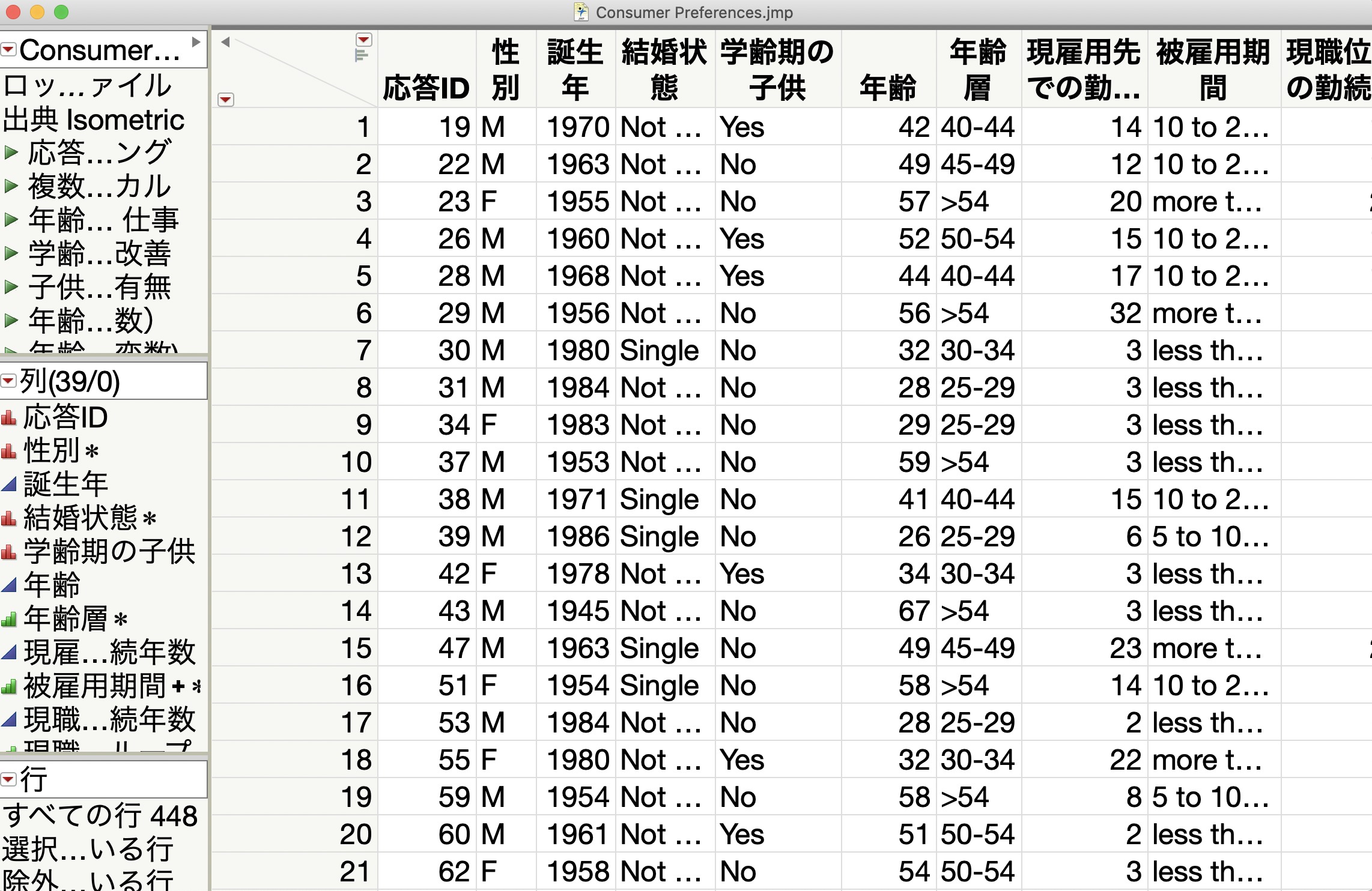
このデータには、一般的な事柄に対する意見や態度についてがまとめられらものです。
ここでは、 年齢層によって「仕事熱心である」かどうかの分布が異なるかどうかを調べて見ましょう。
JMPでのカイ二乗検定
まず、上のメニューバーから[分析] > [二変量の関係]をクリックします。
すると次のウィンドウが出現します。
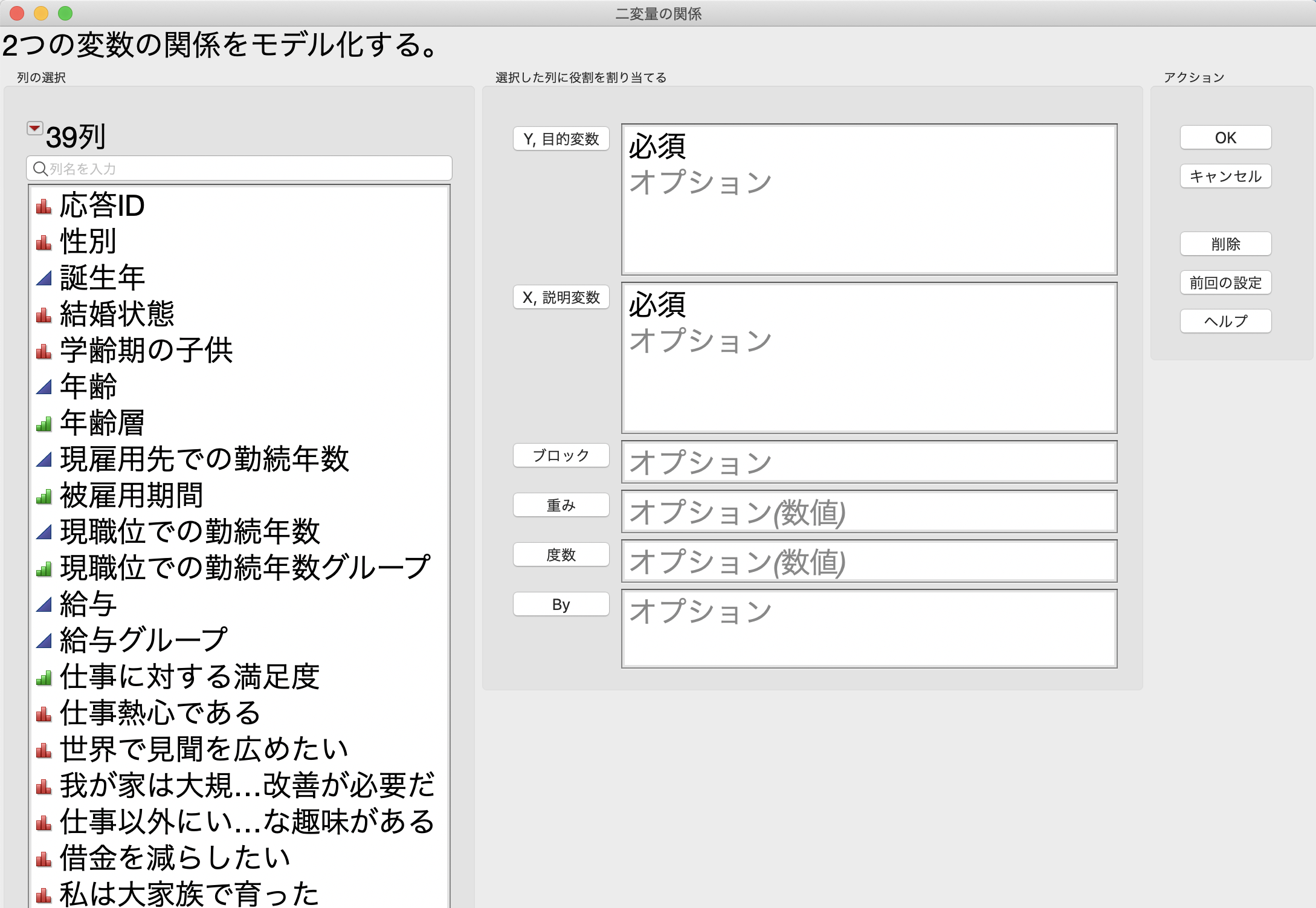
[Y,目的変数]に「仕事熱心である」を選択します。
次に、[X, 説明変数]に「年齢層」を選択します。
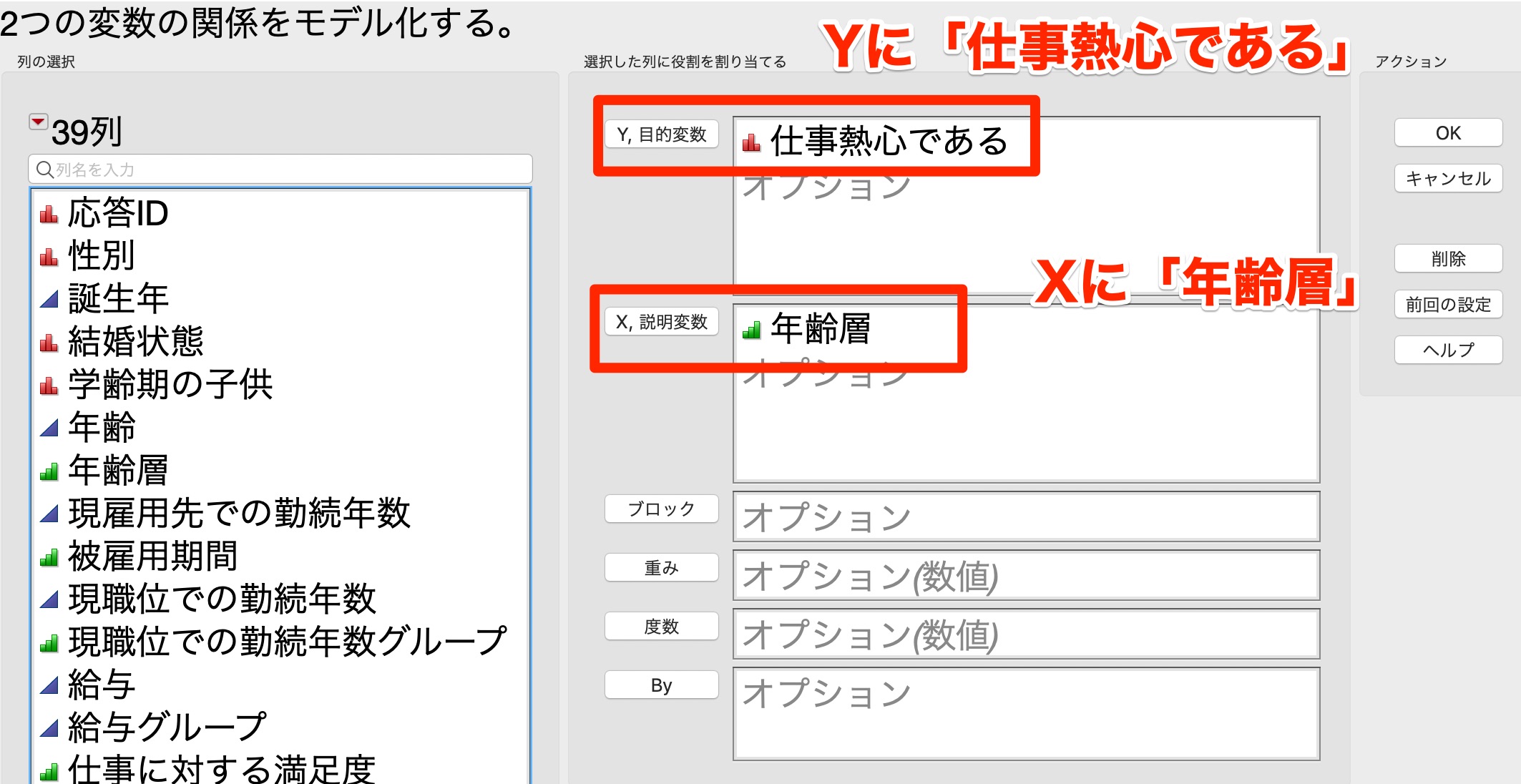
選択ができたら、[OK]をクリックします。
すると、次のようにモザイク図と分割表を含む結果が表示されます。
「分割表」がいわゆるクロス集計表ですね。
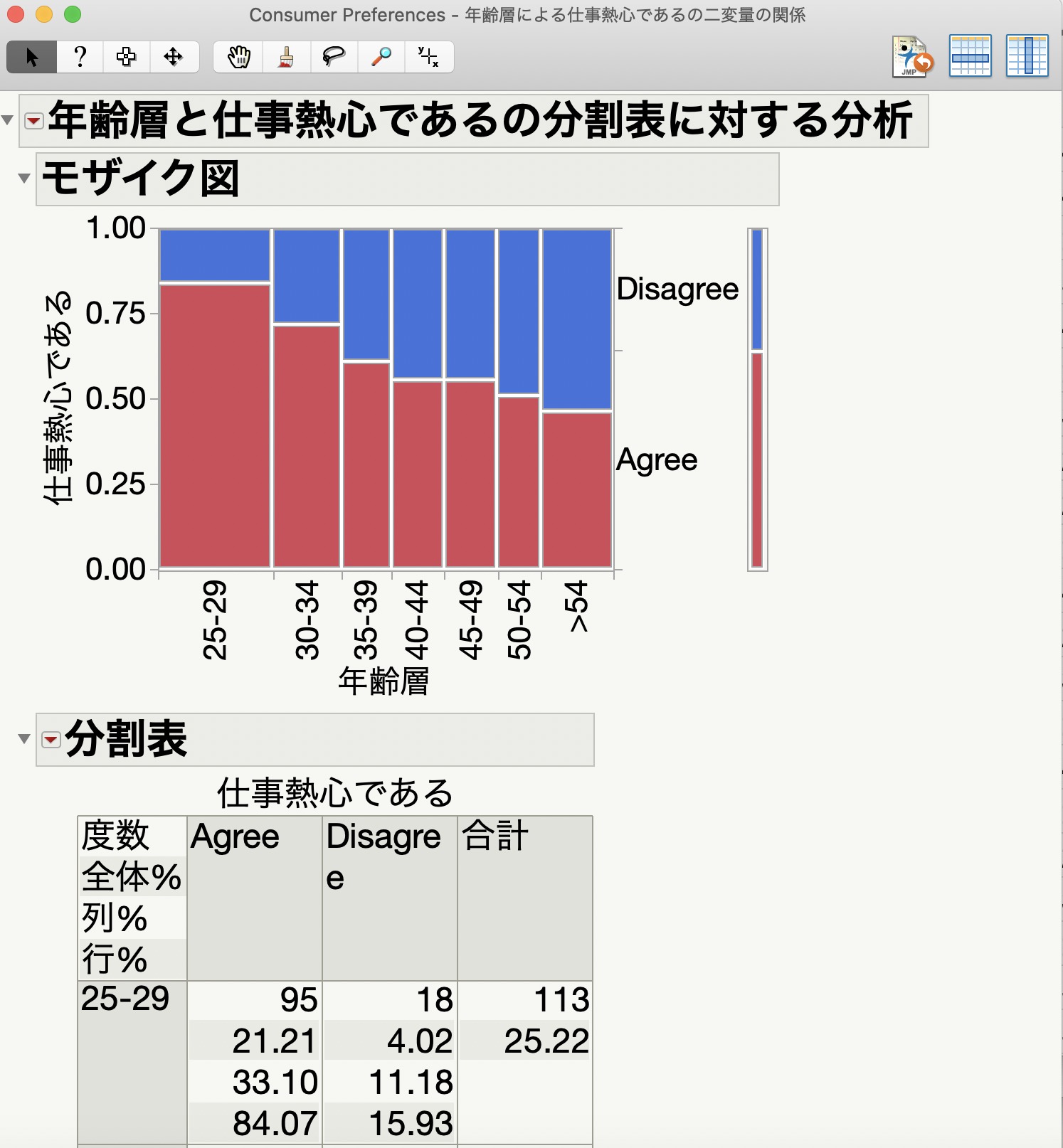
検定結果だけをみずに、モザイク図やクロス集計表の結果を把握しておくことはとても重要です。
そして、この結果の1番下を見ると、カイ二乗検定の結果が出てきています。
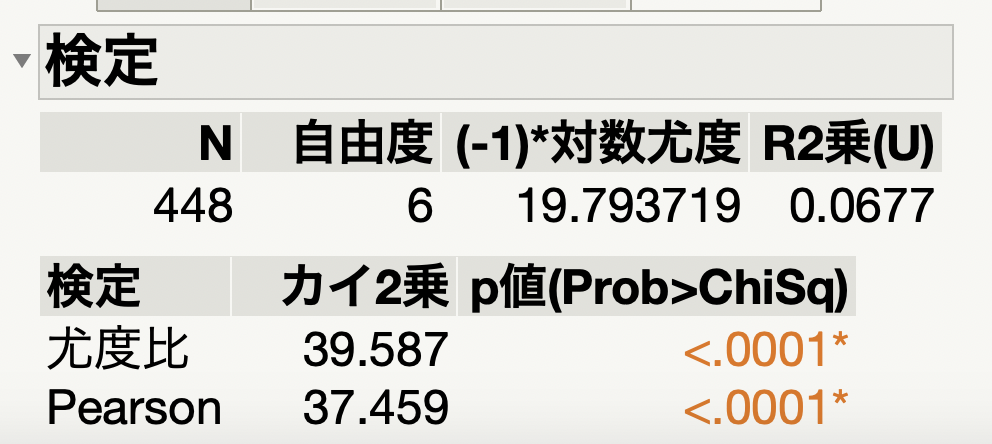
この検定結果を見ると、「尤度比」と「Pearson（ピアソン）」のカイ二乗検定の結果が2つ出力されているのがわかります。
ちょっとだけ違いを説明すると以下の通り。
- 尤度比のカイ二乗検定：観測度数の期待度数に対する比率に基づいてカイ二乗値を計算
- ピアソンのカイ二乗検定：観測度数の期待度数に対する差に基づいてカイ二乗値を計算
こちらのブログで紹介しているカイ二乗検定は、観測度数と期待度数の差に基づく計算なので、いわゆるピアソンのカイ二乗検定です。
一般的にカイ二乗検定といえば、ピアソンのカイ二乗検定を指すことが多いので、JMPで出力される結果に関しても、ピアソンのカイ二乗検定を使うことでOKです。
より厳密に計画を立てるなら、解析計画書（SAP）にどちらのカイ二乗検定結果を使うか明記するのがベストですね！！
JMPでフィッシャーの正確確率検定を行う
次に、JMPでフィッシャーの正確確率検定を行ってみましょう。
JMPでのフィッシャーの正確確率検定は、2×2分割表であれば結果を出力できます。
それ以上の分割表でフィッシャーの正確確率を実施したいとなると、JMP Proが必要になりますのでご注意ください！
というのも、フィッシャーの正確確率検定は近似を用いない方法なので、計算するために統計ソフトにかなりの負担がかかるためです。
フィッシャーの正確確率検定とは
カイ二乗検定と基本的には同じですが、
カイ二乗検定ではカイ二乗分布に近似することを前提に検定を行いますが、
フィッシャーの正確確率検定では組み合わせの計算からp値を計算します。
p値の算出方法が違うため、カイ二乗検定とフィッシャーの正確確率検定では結果が少し異なります。
詳しくは、
>>>フィッシャーの正確確率検定とは？カイ二乗検定と何が違う？分割表の検定
で解説します。
JMPへのデータの読み込み
自分たちのデータを解析する場合は、
[ファイル] > [開く]から解析したデータを開いてください。
ExcelやCSV形式のデータを開くことができます。
この記事では、JMPにすでに用意されているサンプルデータを使います。
[ヘルプ] > [サンプルライブラリー]をクリックします。
すると、次のサンプルデータのディレクトリのウィンドウが出てきます。
今回はカイ二乗検定と同じ” Consumer Preference.jmp”を使います。
JMPでのフィッシャーの正確確率検定
まず、上のメニューバーから[分析] > [二変量の関係] をクリックします。
すると次のウィンドウが出ます。
[Y, 目的変数]に「仕事熱心である」を選択します。
次に、[X, 説明変数]に「性別」を選択します。
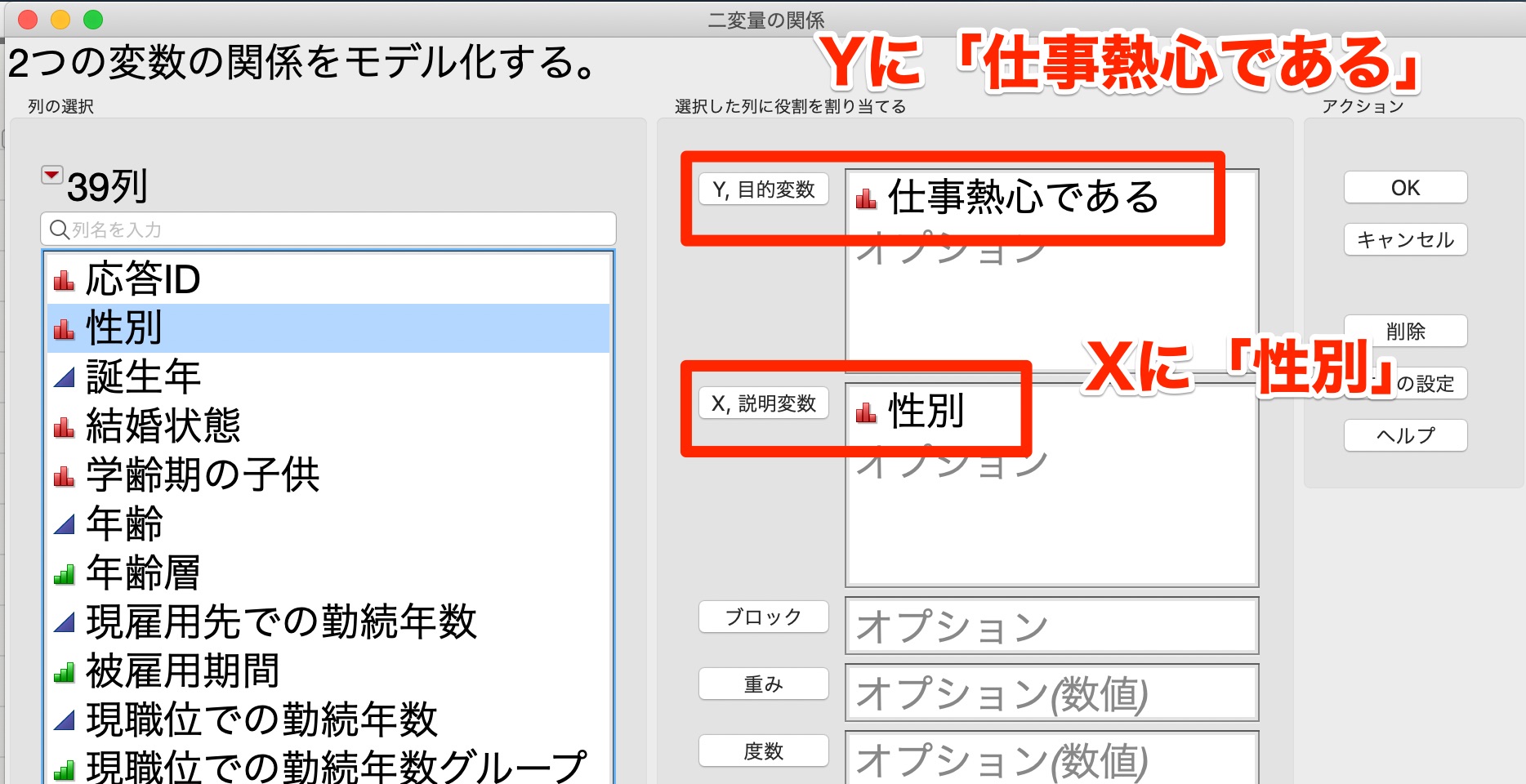
そして、[OK]をクリックします。
すると、カイ二乗検定と同じモザイク図と分割表の結果が出ます。
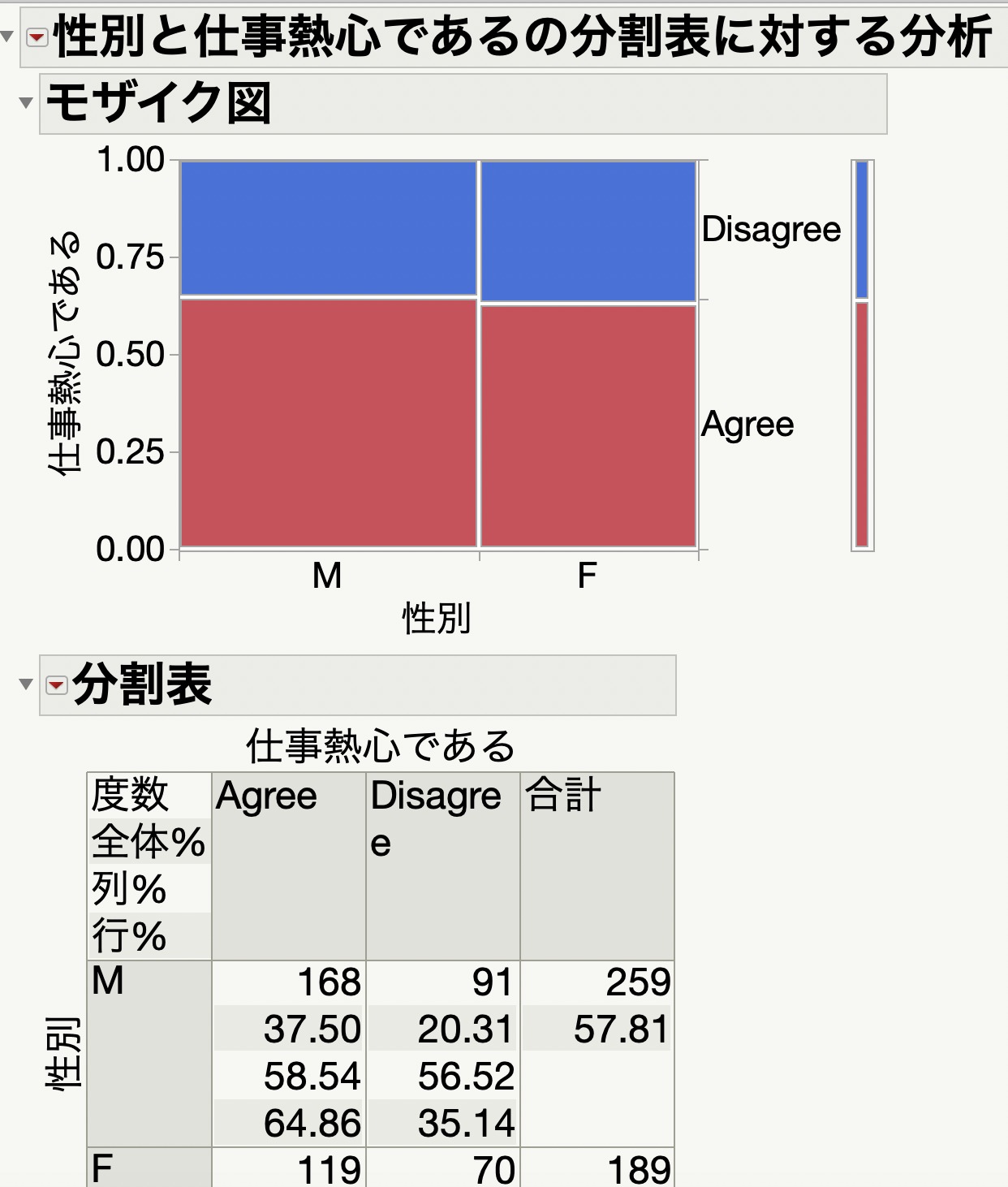
この結果の1番下までスクロールすると、フィッシャーの正確検定の結果が出力されていることがわかります。
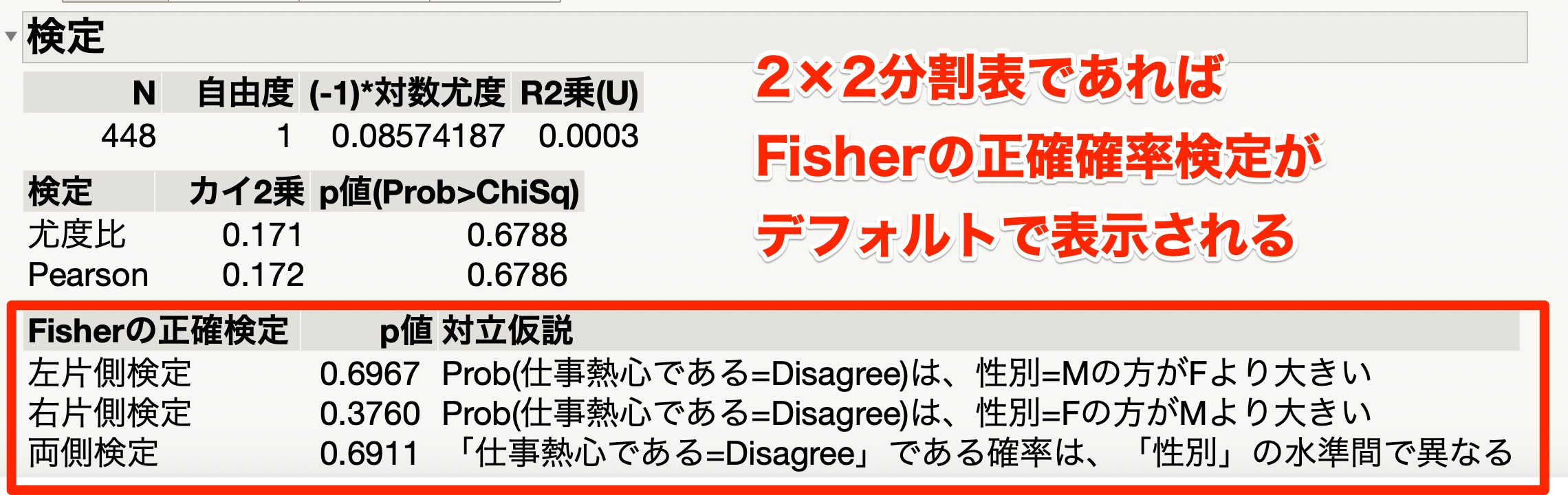
2×2分割表の場合には、フィッシャーの正確確率検定の結果がデフォルトで表示されます。
JMPでカイ二乗検定を実施する方法！まとめ
- Fisherの正確検定は2×2分割表ではJMPで出力できるが、それ以上だとJMP proでしか使えない
- 分割表のカイ二乗検定もFisherの正確検定も[分析] > [二変量の関係]から行う
- カイ二乗検定の結果は期待値と実際の値の間の有意性を表す。
株式会社データシードは、SAS社のJMP事業部と提携しています。
統計解析担当者として10年間色々な統計解析ソフトを試した結果、本当に使いやすいと思ったのがJMPでした。
ぜひあなたもJMPの全機能を30日間試せるトライアル版で、データからさらなる情報を導き出せることを実感してください。
第1章：臨床研究ではなぜ統計が必要なのか？計画することの重要性
第2章：研究目的をどれだけ明確にできるのかが重要
第3章：p値で結果が左右される時代は終わりました
第4章：多くの人が統計を苦手にする理由
第5章：統計を使えるようになるために今日から何をすれば良いか？
第6章：統計を学ぶために重要な環境
もしあなたがこれまでに、何とか統計をマスターしようと散々苦労し、何冊もの統計の本を読み、セミナーに参加してみたのに、それでも統計が苦手なら…
私からプレゼントする内容は、あなたがずっと待ちわびていたものです。
