この記事では「相関係数に対するサンプルサイズ計算を実施する方法!」ということでお伝えしていきます。
- 相関係数についてちょっと復習
- そもそも相関係数に対してサンプルサイズ計算は必要なのか?
- 相関係数に対するサンプルサイズを計算する
- 相関係数に対する事後的検出力を計算する
ということをわかりやすくお伝えしていきますね!
相関係数について復習

まずは相関係数について復習していきましょう。
相関係数は、「2つの連続変数の関連」を数値的に確認する方法です。
相関係数の主な特徴は4つ。
そして、データ解析でよく用いられる相関係数は2つあります。
- ピアソンの相関係数
- スピアマンの相関係数
ピアソンの相関係数はパラメトリックな方法。
2つの連続変数がどちらも正規分布であると仮定して計算するような相関係数です。
一方のスピアマンの相関係数は、ノンパラメトリックな方法。
そのため、必ずしも連続変数が正規分布である必要はありません。
このP値に対して統計学的検定を用いる場合、帰無仮説と対立仮説は以下の通り。
そのため、仮に有意であっても言えることは「相関係数が0ではなさそう」ということだけです。
有意差がある=相関が高い、というのは間違いですので注意してくださいね!
相関係数に対してサンプルサイズ計算は必要か?

そしてそもそも、相関係数に対して事前にサンプルサイズ計算をする必要があるのでしょうか?
サンプルサイズ計算をする意味は、主要な研究目的に対して
- 過剰に被験者を組み入れるのは避ける
- しかし、統計学的なエビデンスを得るほどには多く
というような目的を達成するために事前に計算するもの。
じゃあ、「相関係数を算出することが主要な研究目的であることはあるか?」と問われれば、私の経験上はあまり見ないかなと。
どちらかと言えば、相関係数は探索的に解析するイメージ。
探索的であれば事前のサンプルサイズ計算は必ずしも必須ではないかなと。
そのため、相関係数に対してはサンプルサイズ計算よりも、事後的な検出力を見ることの方が多そうです。
例えば、
- 相関係数が0.5ぐらいあった
- でも有意差が出なかった
- それはサンプルサイズが少なかった(検出力不足だった)ということを示したい
そんな時に、事後的な検出力を計算することになりますので、本記事でも相関係数に対する検出力を計算する方法も併せてお伝えします。
ただ、相関係数に対するサンプルサイズ計算は知っておいて損はないため、サンプルサイズ計算もお伝えしますね。
相関係数に対するサンプルサイズを計算する

では実際に相関係数に対するサンプルサイズ計算をしていきましょう。
使う統計ソフトはSPSSです。
私はよく「SPSS」「EZR」「JMP」の3つの統計ソフトを使いますが、相関係数に対するサンプルサイズ計算ができるのはSPSSだけですね。
(EZRのバックグラウンドにあるRであればきっとできると思います)
ピアソンの相関係数に対するサンプルサイズ計算
まずは、ピアソンの相関係数に対するサンプルサイズ計算をしていきます。
SPSSを立ち上げて、「分析 > 検定力分析 > 相関 > Pearsonの積率」を選択します。
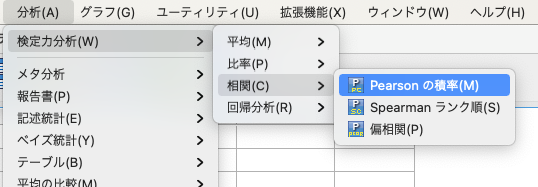
すると以下の画面になりますので、「単一べき乗値」に検出力を、「Pearsonの相関パラメータ」に期待する相関係数を入力します。
(今回は仮に0.3の相関係数を期待するとします。)

OKを押すと、結果として84例必要であるという計算結果が示されました。

スピアマンの相関係数に対するサンプルサイズ計算
まずは、ピアソンの相関係数に対するサンプルサイズ計算をしていきます。
SPSSを立ち上げて、「分析 > 検定力分析 > 相関 > Spearmanランク順」を選択します。
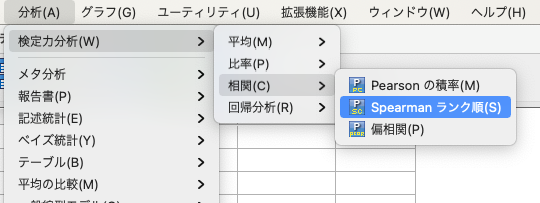
すると以下の画面になりますので、「単一べき乗値」に検出力を、「Spearmanの相関パラメータ」に期待する相関係数を入力します。
(今回は仮に0.3の相関係数を期待するとします。)

OKを押すと、結果として89例必要であるという計算結果が示されました。

相関係数に対する事後的検出力を計算する

では次に、相関係数に対する事後的検出力を計算する方法を実施していきましょう。
想定するのは
という場面です。
ピアソンの相関係数に対する事後的検出力
まずは、ピアソンの相関係数に対する事後的検出力を計算します。
SPSSを立ち上げて、「分析 > 検定力分析 > 相関 > Pearsonの積率」を選択します。

以下の画面で、推定値を「検定力」にしてサンプルサイズを入力し、得られている相関係数を入力します。
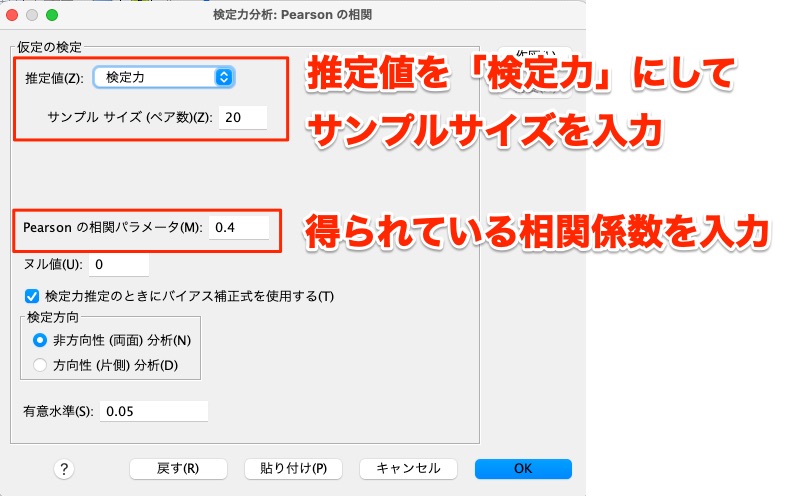
すると、検出力は43%ほどだったことがわかります。

スピアマンの相関係数に対する事後的検出力
まずは、スピアマンの相関係数に対する事後的検出力を計算します。
SPSSを立ち上げて、「分析 > 検定力分析 > 相関 > Spearmanランク順」を選択します。

以下の画面で、推定値を「検定力」にしてサンプルサイズを入力し、得られている相関係数を入力します。

すると、検出力は39%ほどだったことがわかります。

まとめ

いかがでしたか?
この記事では「相関係数に対するサンプルサイズ計算を実施する方法!」ということでお伝えしました。
- 相関係数についてちょっと復習
- そもそも相関係数に対してサンプルサイズ計算は必要なのか?
- 相関係数に対するサンプルサイズを計算する
- 相関係数に対する事後的検出力を計算する
ということが理解できたのなら幸いです!
こちらの内容は、動画でもお伝えしていますので併せてご確認くださいませ。












コメント