この記事では「SPSSで3群のCox回帰を実施!3群間の比較は結果の解釈に注意」としてお送りします。
研究によっては、3群以上の比較をしたい時もありますよね。
そこで今回は、SPSSで3群以上の比較をしたい場合の実施手順と、その結果の解釈方法について解説します。
実施手順自体は全く難しいことはないのですが、結果の解釈がとても重要になりますので、最後まで解説をご覧くださいませ!
SPSSで3群以上のCox回帰は実施できる?

SPSSで3群以上のCox比例ハザードモデル(Cox回帰)を実施できるか?に関しては、結論から言えば、実施可能です。
ただし大きな注意点が2つ必要で、それは
- 結果の解釈の仕方
- 多重性の問題
です。
この2つの注意点に関して詳細な解説は、SPSSで実施後の結果の解釈で詳しく述べますね。
実際にSPSSで3群以上のCox回帰とカプランマイヤー曲線の作成を実施してみる

SPSSで3群以上の場合のCox比例ハザードモデルを実施します。
「3群以上の場合のCox比例ハザードモデル」とありますが、SPSSでの解析手順は2群の場合でも同じですので。
念のため復習ですが、Cox比例ハザードモデルとは、生存時間解析に対する多変量解析でした。
そして今回は架空のデータを使います。
「Treatment(群)」「OS(打ち切りかイベントかの識別フラグ)」「DaysToOS(イベントもしくは打ち切りまでの期間データ)」の3種類のデータが94例分あります。
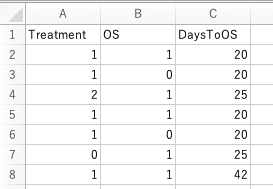
では実際にやっていきましょう!
SPSSにCox比例ハザードモデルを実施するためのデータを取り込む
ではここから、SPSSにデータを取り込みます。
まずは、サンプルデータを適切な場所に保存しておきましょう。
その後、SPSSを開き「ファイル」→「データのインポート」→「CSVデータ」を選択します。
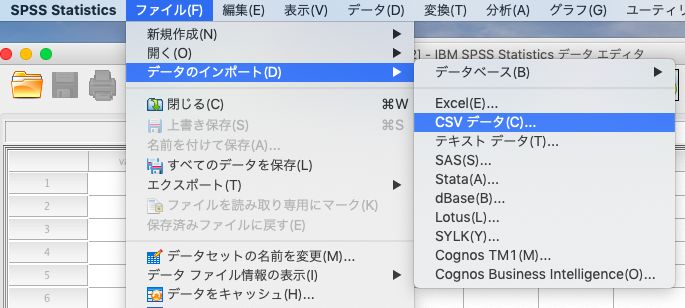
そうすると、以下のような画面になりますので、特にいじらずにOKで大丈夫です。
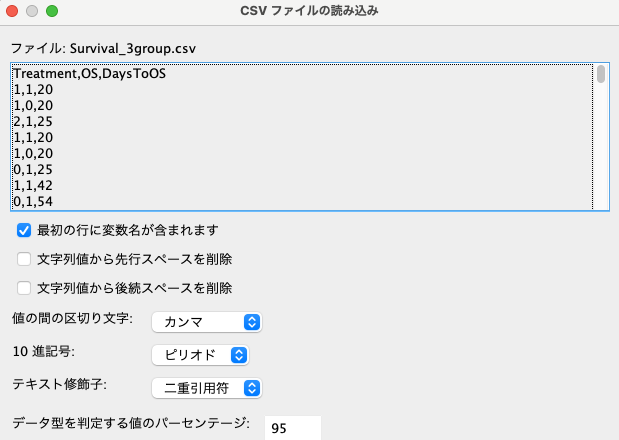
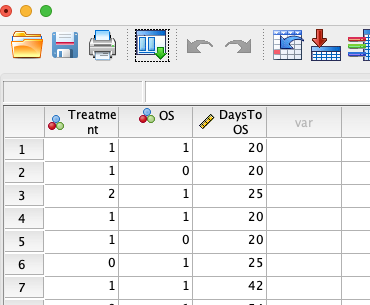
そうすると、以下のようにちゃんとインポートされました。
データの見た目は、エクセルと同じ感じですね。
SPSSで3群以上のカプランマイヤー曲線を作成する
Cox比例ハザードモデルを実施する前に、まずはカプランマイヤー曲線を作成してみましょう。
下図のように、[分析(A)]→[生存時間(S)]→[Kaplan-Meier]の順にクリックします。
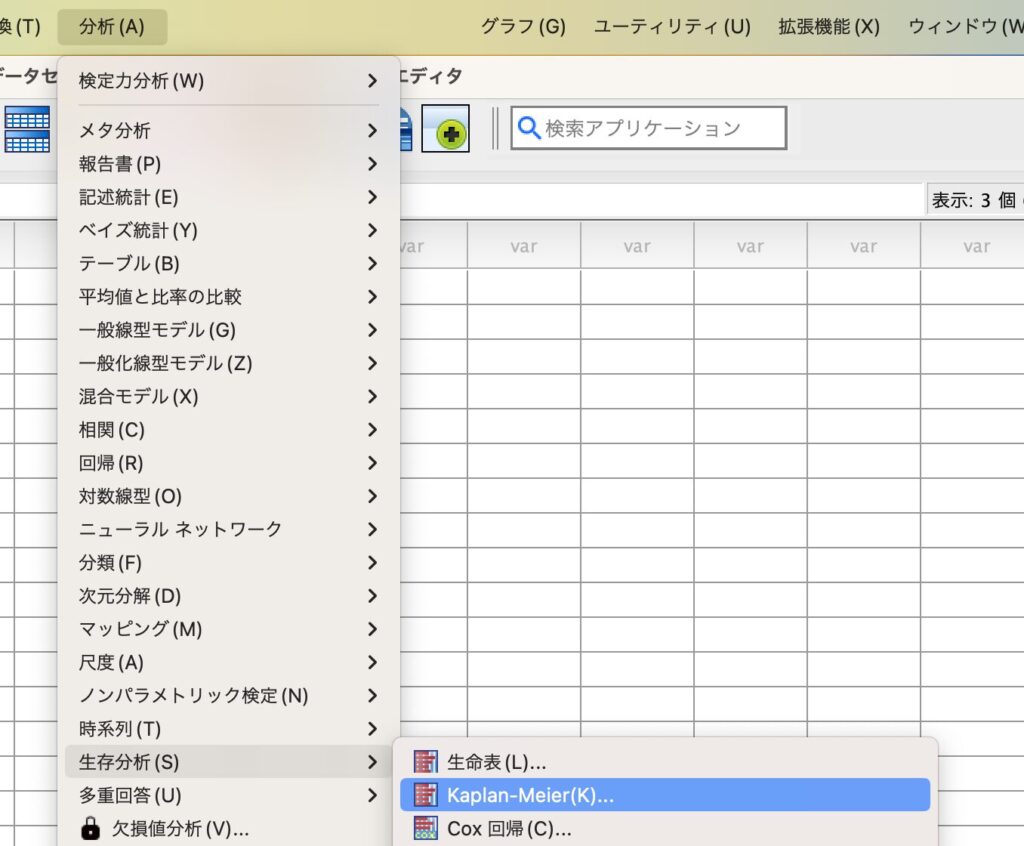
すると以下のボックスが出てきますので、生存変数にDaysToOSを入れ、状態変数にOSを入れ、因子にTreatmentを入れます。
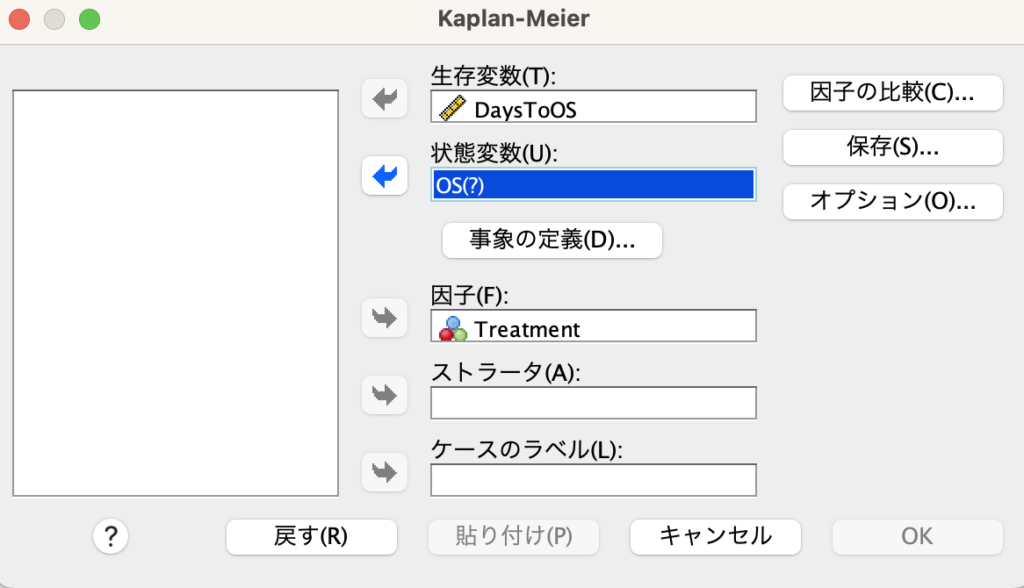
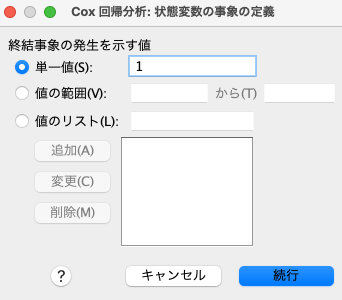
次に、状態変数の「事象の定義」を押します。
すると「終結事象の発生を示す値」が何なのかを指定する必要があることがわかります。
「終結事象の発生を示す値」というのは、いわゆる「イベントの発生を示す値」ということ。
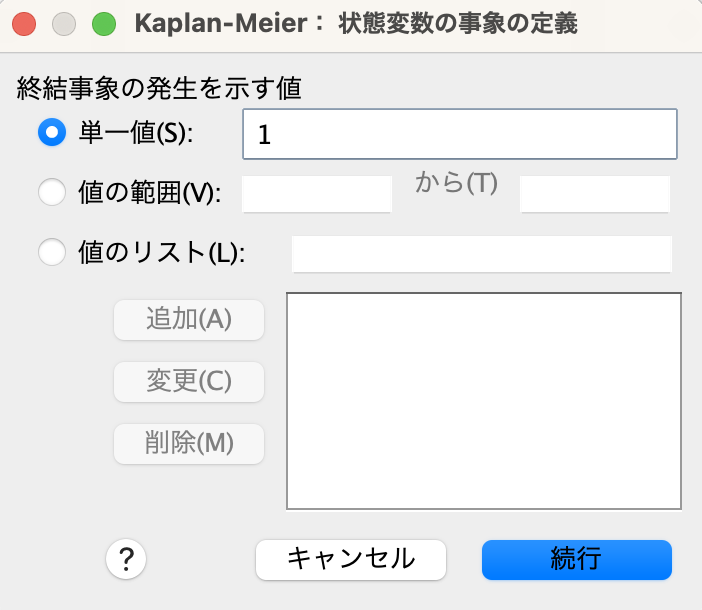
今回はイベントを1、打ち切りを0とした変数になっているため、「終結事象の発生を示す値」に1を指定して「続行」を押します。
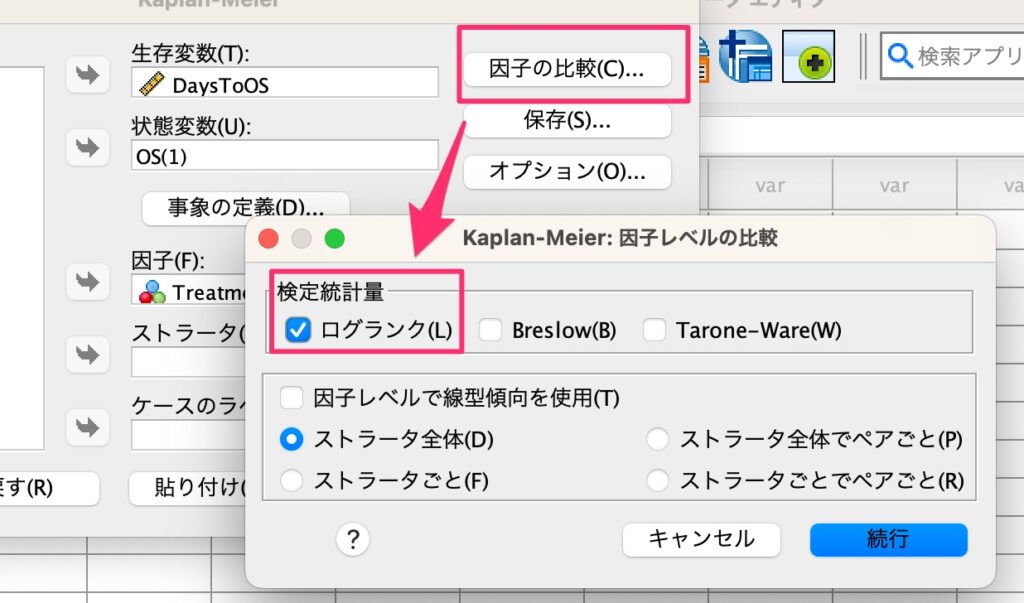
そして、「因子の比較」をクリックして「ログランク」にチェックを入れます。
そして最後に、オプションから「累積生存率」にチェックを入れます。これにより、カプランマイヤー曲線が作成されます。
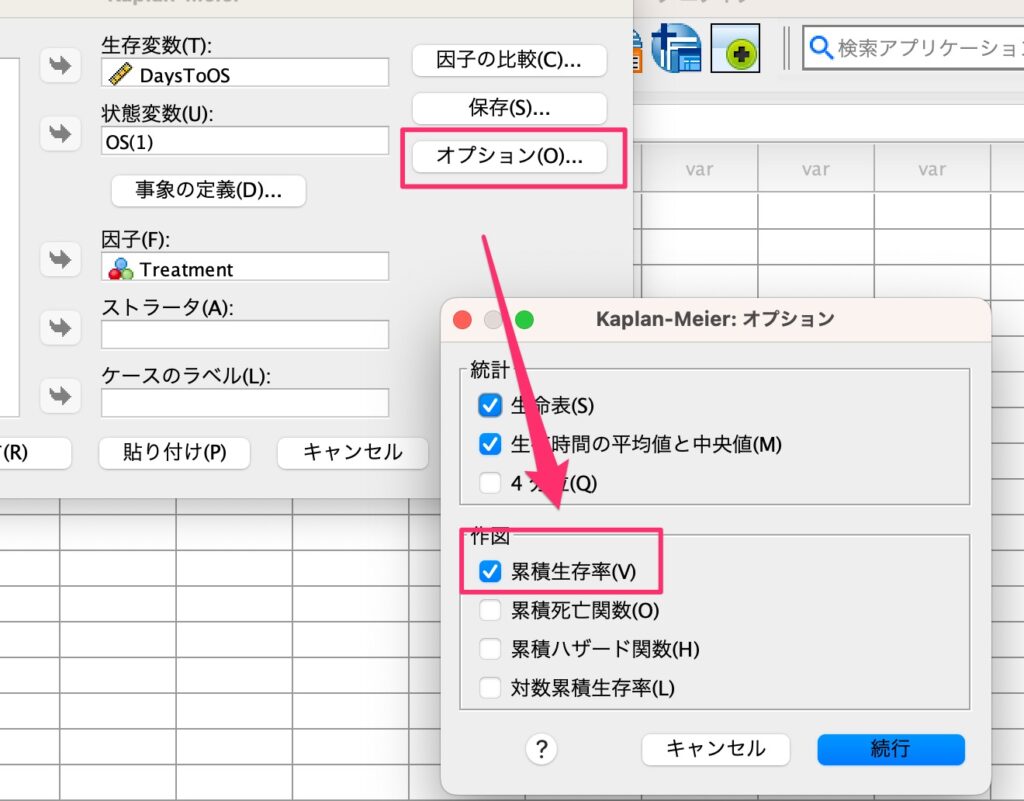
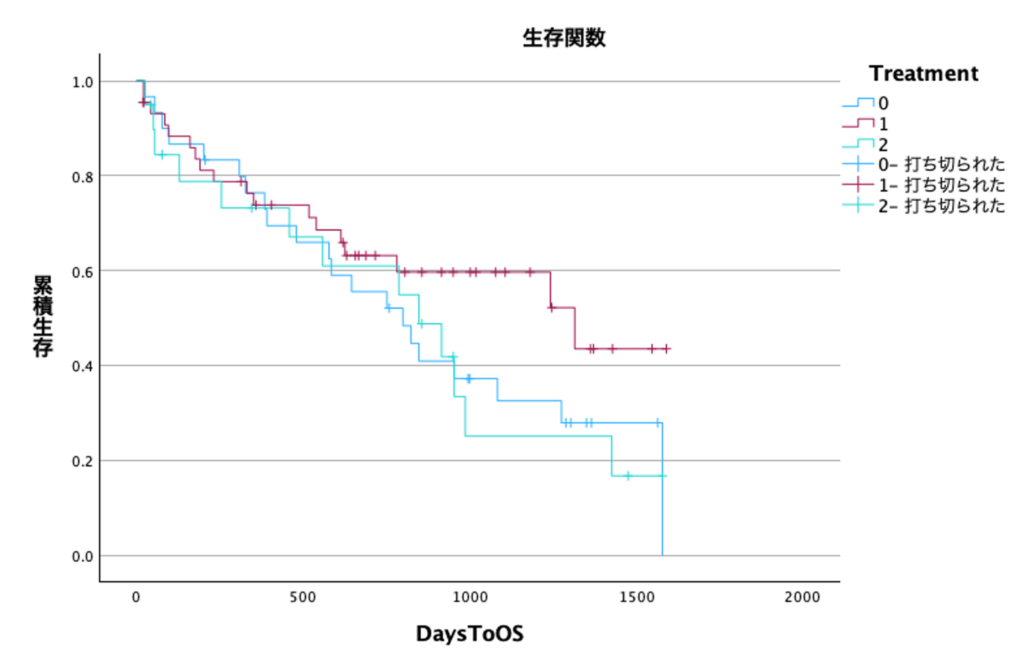
すると、下図のようにカプランマイヤー曲線が作成されました。
SPSSでCox比例ハザードモデルを実践する!
次にSPSSでCox比例ハザードモデルを実施してみましょう。
Cox比例ハザードモデルを実施するには、下図のように、[分析(A)]→[生存時間(S)]→[Cox回帰]の順にクリックします。
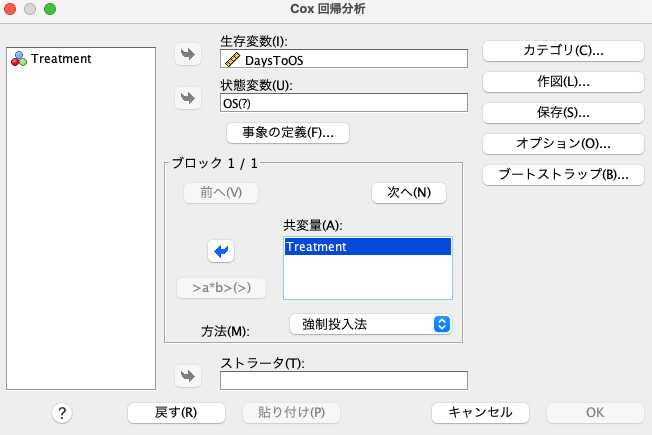
すると以下のボックスが出てきますので、生存変数にDaysToOSを入れ、状態変数にOSを入れ、ブロックの共変量にTreatmentを入れます。
次に、状態変数の「事象の定義」を押します。
すると「終結事象の発生を示す値」が何なのかを指定する必要があることがわかります。
「終結事象の発生を示す値」というのは、いわゆる「イベントの発生を示す値」ということ。
今回はイベントを1、打ち切りを0とした変数になっているため、「終結事象の発生を示す値」に1を指定して「続行」を押します。
そして次に、共変量であるTreatmentは0,1,2という数値が入っていますが、本質的にはカテゴリで扱って欲しい変数のため、Treatmentをカテゴリの変数として指定します。
右上の「カテゴリ」を押すと、下記のようなパネルが出てきますので、カテゴリ共変量として指定して「続行」を押します。
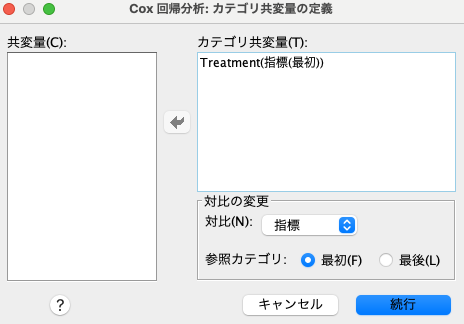
ここまでできたら、後は「OK」を押すだけです。
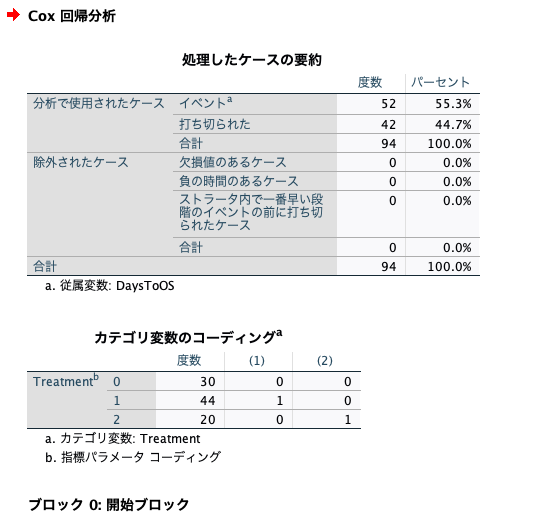
すると、下記のようにCox比例ハザードモデルを実施した結果が出てきました。
3群以上のCox回帰の結果の解釈注意点

実際にSPSSで3群のCox比例ハザードモデルが実施できました。
では、結果の解釈をしていきましょう。
まずは、処理したケースの要約という結果です。
ここでは、イベントの数と打ち切りの数、欠損の数などが出力されます。
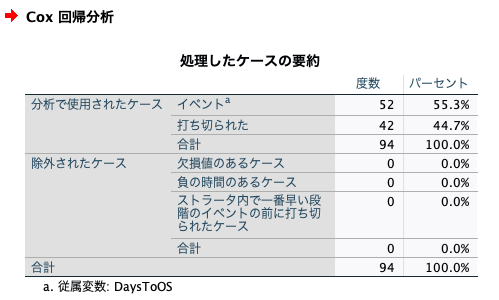
今回はイベントをOS=1に指定しているので、データの中でOS=1の数である52がイベントの数になります。
そして94例分のデータだったため、打ち切りの数は94-52で42例分の打ち切りデータがあるということですね。
欠損値は0でした。
「カテゴリ変数のコーディング」の解釈の仕方
次に注目すべきところが「カテゴリ変数のコーディング」です。
3群以上の比較の場合、この「カテゴリ変数のコーディング」が読み解けなければ、適切な結果の解釈ができません。
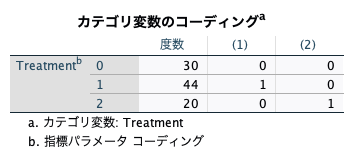
今回の「カテゴリ変数のコーディング」をみると、
- Treatment=0の群は、(1)と(2)ともに0
- Treatment=1の群は、(1)が1で(2)が0
- Treatment=2の群は、(1)が0で(2)が1
ということがわかります。
まず重要なこととして、カテゴリ変数を説明変数にした場合、結果は「ある一つの群を参照群として設定し、参照群と他の群との比較結果が出てくる」ということ。
つまり3群の比較の場合、「参照群 vs 1つの群」「参照群 vs もう1つの群」の2つの結果が出てきます。
4群の場合になると、参照群が一つであり比較する群が3つになるので、3つの結果が出てきます。
じゃあ「参照群がどれ」であり「比較している群がどれ」かが分かれば結果の解釈ができるということ。
SPSSでは、カテゴリ変数のコーディングの中で全て0となっている群が参照群になり、1となっている群との結果を示している、ということです。
なので今回の場合には、(1)と(2)ともに0であるTreatment=0群が参照群となり、(1)の結果は、(1)が1になっているTreatment=1群との比較結果が出力される、ということ。
(2)の結果は、(2)が1になっているTreatment=2群との比較結果が出力される、ということ。
この解釈はとっても重要ですので、ぜひ理解してください!
「モデル係数のオムニバス検定」の解釈の仕方
次に、モデル係数のオムニバス検定を見ていきます。

IBM社の説明を見ると、オムニバス検定は、現行モデル対 Null モデル (この場合は切片) の尤度比カイ 2 乗検定です。0.05 未満の有意確率値は、現在のモデルが Null モデルよりも優れていることを示します。
とありますね。
カイ二乗検定を用いて、いわゆる適合度検定を実施しています。
個人的には、こちらの結果は参考程度に見て、割とスルーしますね。
「方程式中の変数」の解釈の仕方
最後に、方程式中の変数を確認します。
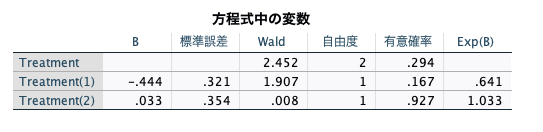
Treatment、Treatment(1)、Treatment(2)の3種類の結果が出ています。
その違いは下記の通りです。
- Treatmentの結果:3群の中でどこかに違いがあるのか?という、分散分析的な解析結果
- Treatment(1)の結果:カテゴリ変数のコーディングで指定された参照群との比較。今回であればTreatment=0とTreatment=1との群比較
- Treatment(2)の結果:カテゴリ変数のコーディングで指定された参照群との比較。今回であればTreatment=0とTreatment=2との群比較
有意確率(=P値)をみると、全ての結果で0.05より大きなP値が出ています。
そのため、Treatment=0とTreatment=1との比較もTreatment=0とTreatment=2との比較も有意差なし、という結果です。
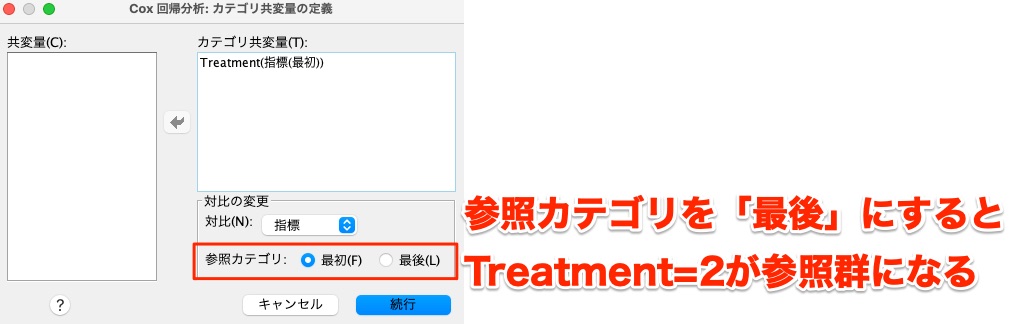
今回は参照群をデフォルトで指定しましたが、もし参照群を変えたい場合、カテゴリ共変量の定義のところで「最後」を指定することも可能です。
その場合、Treatment=2が参照群になります。
3群以上の比較は多重性の問題が発生するので結果の解釈に注意
ここまで見るとわかると思いますが、3群の比較の場合、「参照群 vs 1つの群」「参照群 vs もう1つの群」の2つの結果が出てきます。
4群だと3つの結果が出てきます。
その場合問題になるのが、多重性の問題。
もし多重性の問題に対処するのであれば、閉手順(検定に順番をつけること)かボンフェローニ法などの、有意水準を変える方法を採用することになります。
まとめ

いかがでしたか?
この記事では「SPSSで3群のCox回帰を実施!3群間の比較は結果の解釈に注意」としてお送りしました。
結果の解釈(特にカテゴリ変数のコーディングの解釈)を出来るかどうかがとても重要になりますので、繰り返し見ていただければと思います!











コメント