この記事では、統計ソフトSPSSでオッズ比とリスク比を計算する方法、そして結果の解釈についてお伝えしていきます。
オッズ比やリスク比は、分割表による解析ではメジャーな指標ですよね。
しかし、研究デザインによってオッズ比だけが適切である場面、オッズ比もリスク比もどちらも適切である場面があります。
そのため本記事では
- オッズ比とリスク比を計算するのに適切な研究デザインを整理
- SPSSによるオッズ比とリスク比の計算方法
- SPSSから計算されたオッズ比とリスク比の結果の見方と解釈
についてお伝えしていきます!!
SPSSでオッズ比とリスク比を計算するために、適切な研究デザインを整理

オッズ比とは?という記事でも記載しましたが、医療統計ではオッズ比がよく使われます。
その理由の一つが「オッズ比は研究デザインにかかわらず使うことができる」という点。
研究デザインは、大きく分けて「前向き研究」と「後ろ向き研究」に分けることができます。
この時、オッズ比とリスク比の使い分けの結論は下記の通り。
| リスク比 | オッズ比 | |
| 前向き研究(コホート研究) | ◯ | ◯ |
| 後ろ向き研究(ケースコントロール研究) | × | ◯ |
前向き研究ではオッズ比もリスク比も使える
前向き研究は「現時点から未来に向かって調査する研究」のことです。
例えば、ガンがない人をランダムに500人選び、現在喫煙をしているかどうかを調査し、2年間追跡する。そして、喫煙の有無別にガンが発生したかを追跡調査する。
この時、調査開始時点ではガンは発生しておらず、それから2年後(未来)にガンの発生を調べます。
このような研究を前向き研究といい、別の言い方だとコホート研究といいます。
この研究は2年後の未来へ向かって調べる研究であり、「前向き」の研究といいます。

前向き研究の場合、オッズ比もリスク比もどちらも使えます。
後ろ向き研究ではオッズ比しか使えない
一方の後ろ向き研究はというと、「現時点から過去に遡って調査する」という研究。
<例えば、ガンであると診断された250人と、ランダムに選ばれたガンではない250人について、過去の喫煙の有無を調査する。
すでにガンがあると診断された人、ガンではない人がいて、その時点から過去にさかのぼって喫煙をしていたかどうかを調べます。
このような研究を後ろ向き研究といい、別の言い方ではケースコントロール研究といいます。

後ろ向き研究では、オッズ比は使えますがリスク比は使えません。
詳しくはオッズ比とは?という記事を参照していただきたいですが、理由を簡潔にいうと後ろ向き研究だと選んでくるサンプル数が異なるとリスク比も違った結果になってしまう、ということが起こるからです。
一方のオッズ比は、そのような性質がないため、後ろ向き研究でも問題なく使うことができます。
ということで、あなたのデータが前向き研究で得られたデータなのか、後ろ向き研究で得られたデータなのかによって、リスク比を算出することがOKかNGか決まりますので、そこだけ注意してくださいね!
SPSSでオッズ比とリスク比を計算しよう!

では今回は、前向きのコホート研究で得られたデータとして、オッズ比とリスク比をSPSSで計算していきましょう。
下記のような分割表があったとします。
216人を対象に、喫煙の有無と肺がんの関係について調査したデータ、という想定です。
| 肺がん患者 | 対照 | 合計 | |
| 喫煙歴あり | 68 | 49 | 117 |
| 喫煙歴なし | 40 | 59 | 99 |
| 合計 | 108 | 108 | 216 |
SPSSで計算する前に、手計算でオッズ比とリスク比を出してみる
実は、オッズ比もリスク比も計算の仕方が簡単なので、手計算でも簡単に計算可能です。
- 喫煙歴あり群のオッズは、68/40。
- 喫煙歴なし群のオッズは、40/59。
- 喫煙歴あり群のリスクは、68/117。
- 喫煙歴なし群のリスクは、40/99。
そのため、オッズ比は
(喫煙歴あり群のオッズ)/(喫煙歴なし群のオッズ)
=(68/40)/(40/59)
=2.05
となります。
一方のリスク比は
(喫煙歴あり群のリスク)/(喫煙歴なし群のリスク)
=(68/117)/(40/99)
=1.42
となります。
オッズ比とリスク比だと数値が異なりますので、事前にどちらの指標を使うのかを研究の計画段階で決めておく必要がありますね。
SPSSでオッズ比とリスク比を算出する
では、実際にSPSSでオッズ比とリスク比を算出してみましょう。
オッズ比もリスク比も分割表の計算なので、SPSSでカイ二乗検定を実施した時のようなデータを用意することが望ましいです。
しかし、すでに上記で分割表の形式で与えられているデータに対しては、わざわざ1行1被験者とするデータを作るのが面倒。
なので、もう少し簡単な方法をお伝えしますね。
新規のデータテーブルから下記のように、1列目に「喫煙歴の有無」、2列目に「肺がんの有無」、3列目に「それぞれの組み合わせに対応した人数(度数)」を入力します。
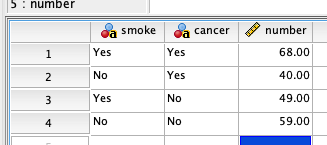
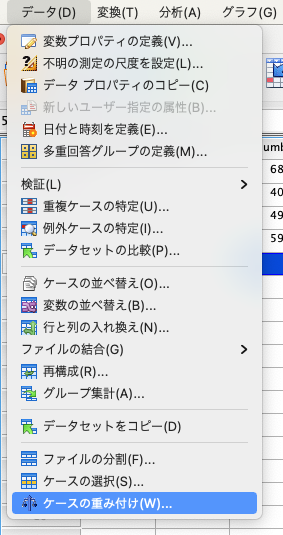
そして、[データ]→[ケースの重み付け]をクリックする。
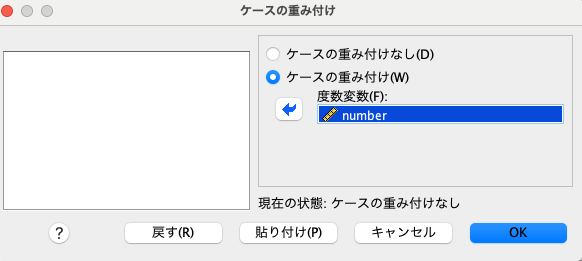
ダイアログボックスが現れるので、[ケースの重み付け]をチェックし、度数の列であるnumberをクリックして[度数変数]に移動させる。
OKを押すと画面の右下に[重み付きオン]と表示されていることがわかる。
そして、ここからがオッズ比とリスク比の計算。
[分析]→[記述統計]→[クロス集計表]をクリックします。
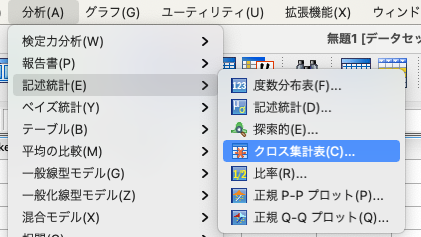
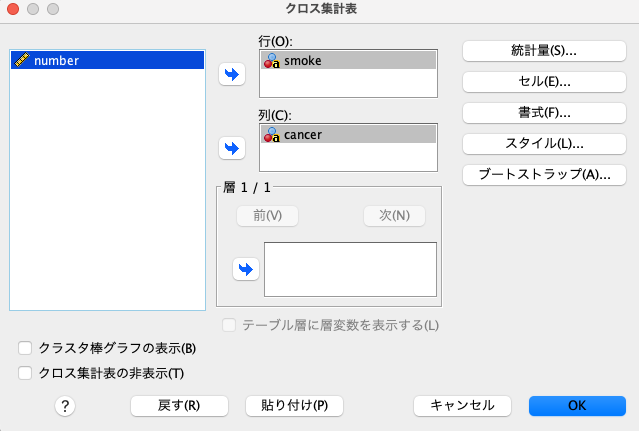
そして、行に「smoke」を選択し列に「cancer」を選択します。
度数が入っているnumberはどこに入れればいいの?と思うかもしれませんが、ケースの重み付けをしている時点で考慮しているので、ここではnumberに対して何もしなくて大丈夫です。
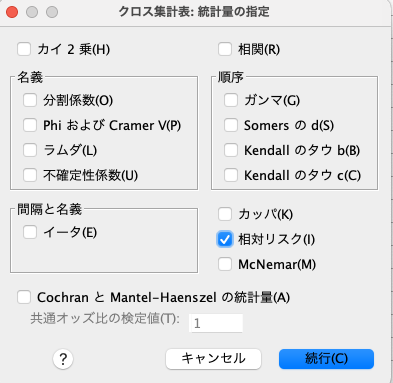
そして、「統計量」をクリックして相対リスクにチェックを入れます。
相対リスクとは、リスク比と同じ意味です。
そして続行を押すと、SPSSにリスク比とオッズ比が算出されます。
SPSSで計算されたオッズ比とリスク比の結果の見方と解釈
計算結果を示します。
重要なのは「クロス表」と「リスク推定」の部分ですね。
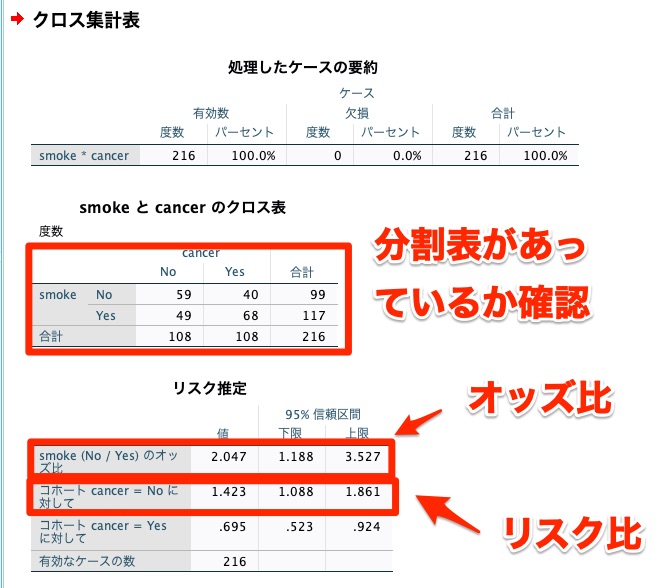
念のため、分割表が意図したものと合っているかを確認しましょう。
その後、「リスク推定」の部分で、オッズ比とリスク比を確認します。
オッズ比は2.047であり、リスク比は1.423なので、手計算で算出したものと一致しましたね。
ちなみにオッズ比にもリスク比にも95%信頼区間が出力され、どちらも1を跨いでいないので、もし仮に有意水準を5%と設定した場合には有意な差があると言えます。
(1は帰無仮説の値(=差がないときの値)ですね。)
まとめ

この記事では、統計ソフトSPSSでオッズ比とリスク比を計算する方法、そして結果の解釈についてお伝えしました。
具体的には
- オッズ比とリスク比を計算するのに適切な研究デザインを整理
- SPSSによるオッズ比とリスク比の計算方法
- SPSSから計算されたオッズ比とリスク比の結果の見方と解釈
についてお伝えしましたので、ぜひご自身の研究にお役立てください!











コメント