この記事では統計ソフトSPSSを使用して、クラスカルウォリス（Kruskal-Wallis） 検定の実施方法と分析結果の解釈を行います。
クラスカルウォリス（Kruskal-Wallis） 検定は1元配置分散分析に対応したノンパラメトリックな手法ですね。
そのため、クラスカルウォリス（Kruskal-Wallis） 検定を使う時の注意点としては、たとえ有意差が出たとしても「どこかの群に違いがある」ということまでしか言えず、「具体的にどの群間に違いがあるのかはわからない」ので、その点だけはご注意ください！
SPSSでクラスカルウォリス検定（Kruskal-Wallis）を実施！適用の条件はある？
上述の通り、クラスカルウォリス（Kruskal-Wallis） 検定は1元配置分散分析に対応したノンパラメトリックな手法です。
まずはクラスカルウォリス（Kruskal-Wallis） 検定の適用条件を整理しましょう。
- 連続量のデータであること
- 対応のないデータであること
- 3群以上の標本を対象としたデータであること
ノンパラメトリックなので、条件が少ないですね。
SPSSによるクラスカルウォリス（Kruskal-Wallis） 検定
まずは今回使用するデータを読み込みます。
使用するデータは、SPSSをダウンロードするとサンプルデータとしてついてくるpain_medication.savです。
このようなデータですね。
今回は「健康状態の違いが治療までの時間の違いをもたらしているのか？」という疑問を持ったとして解析を進めていきます。
つまり、説明変数と目的変数を整理すると
- 説明変数：健康状態（1：悪い、2：普通、3：良い）
- 目的変数：時間（効果までの時間）
となりますね。
それでは実際に分析してみましょう。
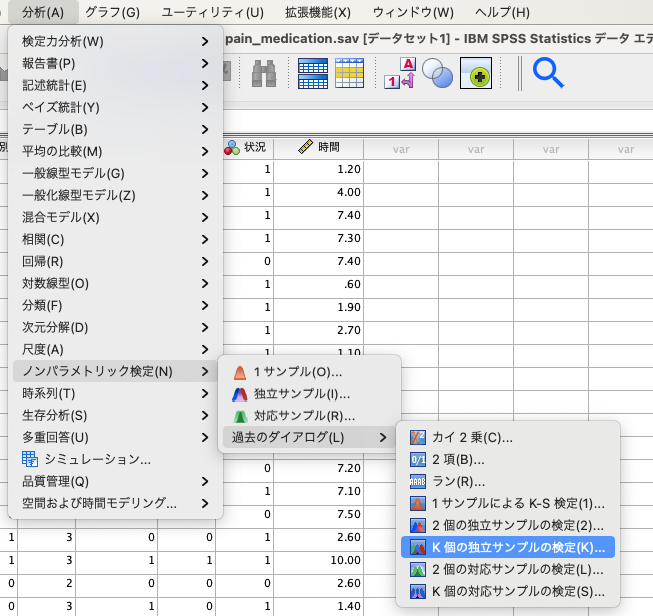
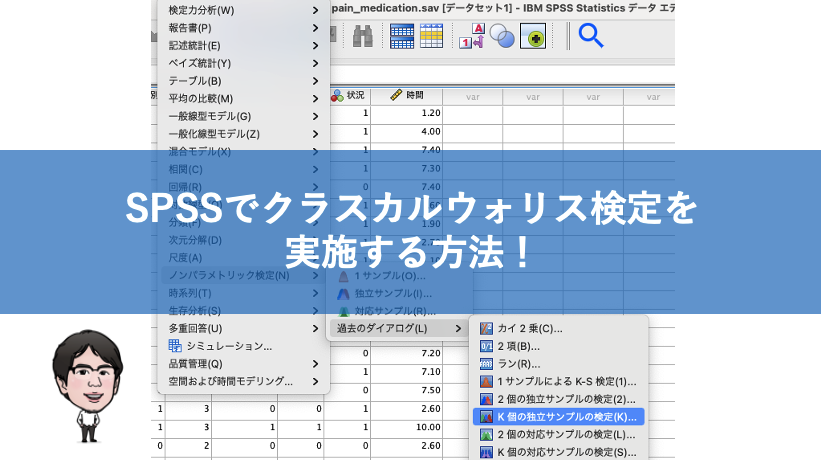
下図のように、[分析(A)]→[ノンバラメトリック検定(N)]→,[過去のダイアログ]、[Ｋ個の独立サンプル]の順にクリックします。
下図で、差を見たい変数である「時間」を[検定変数リスト(T)]に追加し、「健康」を[グループ化変数(G)]に追加します。
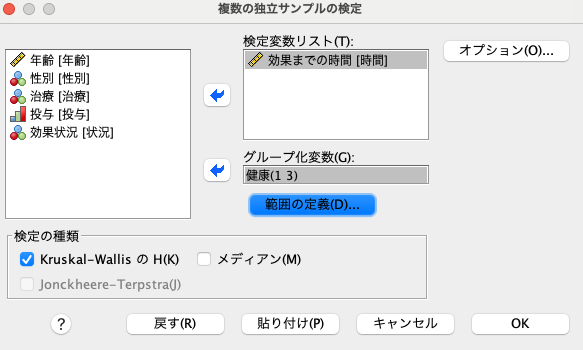
そして[範囲の定義(D)]をクリック。
新たなダイアログボックスで[最小]と[最大]のそれぞれ範囲内に、健康のカテゴリー数値の範囲を入れます。
健康のカテゴリー（3種類）には”1〜3″を割り当ててあるため、[最小]を1、[最大]を3と入力し、OKをクリックします。
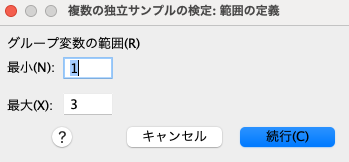
SPSSでクラスカルウォリス（Kruskal-Wallis） 検定を実施する方法は以上です！
SPSSによるクラスカルウォリス（Kruskal-Wallis） 検定を実施した結果を解釈する
SPSSでクラスカルウォリス（Kruskal-Wallis） 検定を実施すると下図のような結果が出力されます。
この他にも表が出力されるはずですが、とりあえず示したところだけ見れば十分。
今回の結果は、[漸近有意確率]がp=0.368なので有意差がない結果ですね。
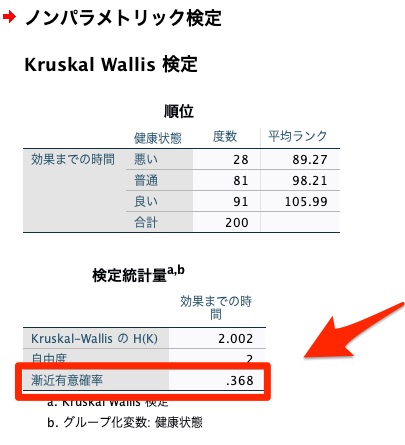
有意差がないということは、健康状態の違い（悪い、普通、良い）によって効果までの時間の分布には差があるとは言えない、という結論になります。
決して、健康状態の違いによって効果までの時間の分布が同じ、ではないので注意してくださいね。
まとめ
今回はSPSSを用いて、一元配置分散分析のノンパラメトリック版であるクラスカルウォリス検定を行いました。
対応のあるノンパラメトリックな検定ということで、適用条件は以下の二つでしたね。
- 連続量のデータであること
- 対応のないデータであること
- 3群以上の標本を対象としたデータであること
ぜひ結果の解釈までご自身でできるようになっていきましょう！
コメント