SPSSでカイ二乗検定！フィッシャーの正確確率検定との違いやP値の解釈も

この記事では統計ソフトSPSSを使ってカイ二乗検定の実施方法と分析結果の解釈を行います。

SPSSによるカイ二乗検定では分割表（クロス集計表）と呼ばれる表を基に考えていく検定方法となります。

それではSPSSでのカイ二乗検定について具体例を基に考えていきましょう！

カイ二乗検定とは？

例えば、「運動習慣の有無」と「性別」の関連を調べなければならないとします。

そこで、運動習慣のある人は男性に多いのではなかろうか?

とか、運動習慣のない人は女性に多いのではなかろうか?

という行と列の関連性を知りたいときに、カイ二乗検定（カイ二乗独立性の検定とも言います）を用います。

この記事ではSPSSでのカイ二乗検定の実施方法について具体的に説明していきます。

カイ二乗検定を実施するのに必要な知識：分割表（クロス集計表）

SPSSでカイ二乗検定を行うには上の表のような分割表（クロス集計表）を用います。

上の分割表は2行2列になっているので、「2×2分割表」と呼びます。

上記の表の例では男女合わせて40人（男性20名、女性20名）を対象としています。

仮に、性別と運動習慣の有無が全く関係ないとすれば、理論的に各セルは10人ずつ均等に該当するはず・・・ですよね？

(よりわかりやすく言えば、女性—運動習慣あり10人、女性—運動習慣なし10人、男性—運動習慣あり10人、男性—運動習慣なし10人に均等に分かれるはずです。）

この理論的に各セルが均等になるはずの「10人」という度数(人数)を期待度数と言います。

表に示される通り、実際の人数（観察度数）は、女性-運動習慣ありが8人、女性一運動習慣なし12人、男性一運動習慣あり14人、男性一運動習慣なしが6人なので、

これらのうちどのセルの人数が統計的に期待度数よりも多い、または少ないということについてカイ二乗分布の値を利用して検定するのがカイ二乗検定になります。

カイ二乗検定に適用できるデータの条件とは

カイ二乗検定を用いることができるデータの条件は以下の通りです。

• 名義尺度のデータであること。
• 順序尺度のデータでも適用となる(ただし段階数が多くないとき)。

SPSSでカイ二乗検定とフィッシャーの正確確率検定を実施する

それではSPSSを使ってカイ二乗検定を行っていきましょう。

同時にフィッシャーの正確確率検定もできますので、一緒に解説しますね。

まずは今回使用するデータを読み込みます。

今回のデータは、SPSSをインストールした際に付属しているサンプルデータを使います。

今回はサンプルデータのadl.savを使います。

adl.savは、脳卒中患者のリハビリ効果判定データです。

データを表示させた後、下図のように[分析]→[記述統計]→[クロス集計表]を選択するとウィンドウが表示されます。

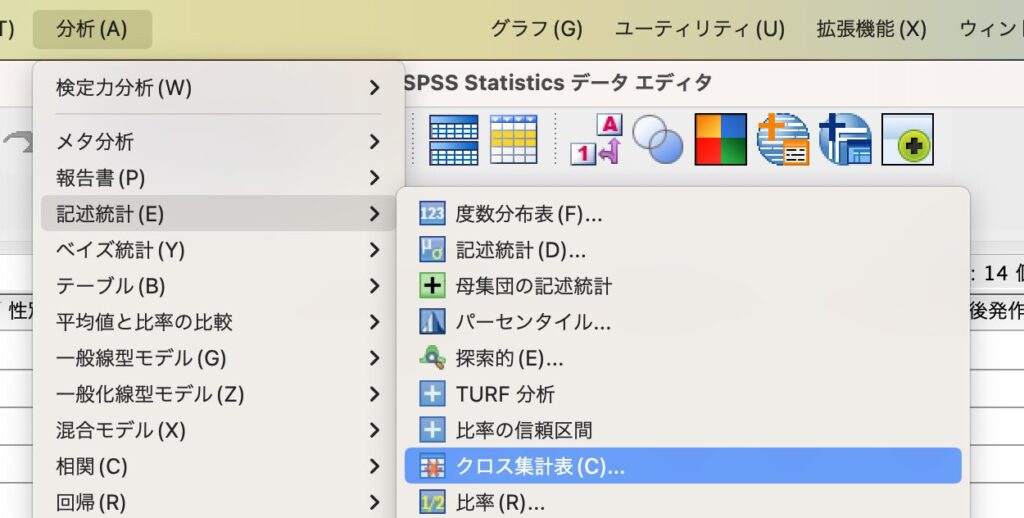
「治療グループ」、「退院後の発作」の各データを[行]と[列]のボックスに矢印➡か、ドラッグ＆ドロップで入力します。

その後、[統計量]をクリックしたら[統計量の指定]のウィンドウが表示されるので、[カイ2乗]にチェックを入れ[続行]をクリックします。

次に、[セル]をクリックすると[セル表示の設定]のウィンドウが表示されます。

そこで、[観測]、[調整済みの標準化]にチェックを入れ、[続行]をクリックします。

最後に[クロス集計表]のウィンドウに戻ったところで[OK]をクリックすると分析が始まります。

SPSSで出力したカイ二乗検定結果の読み方

上記の通りにカイ二乗検定を実施すると、問題なく結果が表示されます。

まずは、上の表の①「a.0セル(0.0%)は期待度数が5未満です」の”0セル“の値を見ます。

この①の値が0セルとなっているときは、表中②の[Pearsonのカイ2乗]の[漸近有意確率(両側)]で判断してOKです。

一方、この①の値が0セル以外となっているときは、表中③の[Fisherの直接法]の結果で判断します。

この結果では0セル(0.0%)なので、表中②で判断します。

表中②の[Pearsonのカイ2乗]の[漸近有意確率(両側)]がカイ二乗検定の結果そのものになります。

もし期待度数が5未満のセルがあれば、③のフィッシャーの正確確率検定の結果を見るのが良いですね。

②または③がp<0.05さらにはp<0.01であったときは、分割表のどこの頻度が有意に多く、どこの頻度が有意に少ないかを見ます。

そういった場合は④の[調整済み残差]を参照します。

特に、3群以上ある場合のカイ二乗検定の場合には、この部分に着目することは重要。

この値が2(正確には1.96)以上のときは有意に他の頻度よりも多いと判断し、-2(正確には-1.96)以下のときには有意に他の頻度よりも少ないと判断します。

いわゆる、残差分析の結果が表示されているということになります。

今回の分析結果では[Pearsonのカイ2乗]の[漸近有意確率(両側]の値が有意ではない(p=0.786)ので[調整済み残差]を見るまでもないですが、、、、

カイ二乗検定の結果を論文やレポートに記載する方法

結果を論文やレポート等に記載する時は、

例えば

「運動習慣の有無と性別の関連についてカイ二乗検定を実施したところ、p=0.057で有意差は得られなかった。また調整済み残差による頻度の差も見られず、関連度を表す連関係数φ＝-0.302で有意ではなかった」

と記載すればいいですね。

フィッシャーの正確確率検定との違いは？

分割表の検定としては、カイ二乗検定の他にフィッシャーの正確確率もあります。

カイ二乗検定とフィッシャーの正確確率検定の違いは「P値の出力の方法が違う」ということ。

カイ二乗検定では「カイ二乗値」という統計量をいったん経由してから、P値を出力します。

つまりカイ二乗検定は、「近似した方法」と言えます。

一方のフィッシャーの正確確率検定は「正確にP値（確率）を計算する方法」ということ。

なので、カイ二乗検定とフィッシャーの正確確率検定ではP値が若干異なります。

SPSSでカイ二乗検定まとめ

今回はカイ二乗検定を実施しました。

キーワードは、クロス集計表、Pearsonのカイ二乗の有意確率、調整済み残差、連関係数φですので用語の意味をしっかりと理解しましょう。

そして、SPSSによる実際の分析の仕方を繰り返し復習してみてください。

＞＞SPSSでT検定を実施する方法

＞＞SPSSで分散分析（ANOVA）を実施する方法